把数组排成最小的数

题目

　　输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

思路

一　

需要找到字典序最小的哪个排列我求出所有的排列，然后排序后取最小。进一步转化问题为全排列问题,请参考https://www.cnblogs.com/tianzeng/p/10055489.html，只不过参与排列的元素为字符串了，而不在是单纯的单个字符。 以下内容为最优的求全排列的解法，包含如何对于重复元素的处理防止不必要的处理操作。可以把排列问题分成固定第一个位置，剩余元素全排列问题。之后对剩余元素又进行同样的处理，固定第一个位置，剩余元素全排列。如图： 

 

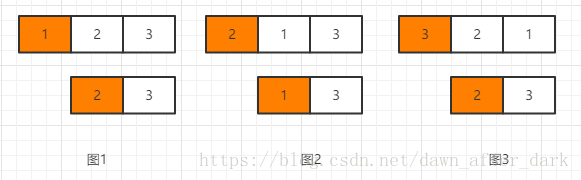
第一个想法可能就是遇到与第一部分元素相等，就不交换。比如abb, 第一个位置可分别于第二个，第三个位置交换，因为他们都不与a相同，得到 abb, bab, bba。 考察第二位置时，对于bab，第二位置会与第

三个位置交换，得到bba。而bba已在与第一位置交换的过程中出现过了。所以单纯的看交换元素是否相等是不行的。 有重复的出现的原因为，已经有b在第一个位置出现过了，不能在有相同的元素交换到此位

置上，即不能有重复的元素作为排列问题的第一部分，这肯定会导致重复的子问题产生。所以对于每一个位置遍历，我们添加一个set用于记录以在该位置出现过的元素。

二

　　给出两个整数m，n，把它们拼接成mn，nm，比较他们的大小。m，n都是int类型，但是把他们拼接后就可能溢出，这是一个隐形的大数问题，所以要用字符串来解决问题。把他们拼接成字符串mn,nm后，他们的位数可定时相同的，所以比较他们的大小就可以了。要注意的是字符串的比较函数需要重新定义，不是比较a和b，而是比较ab与 ba。

1. 若ab 大于 ba 则 a 大于 b，
2. 若ab 小于 ba 则 a <小于b，
3. 若ab 等于 ba 则 a 等于 b；

如 6 61 因为 61 6 <6 61 所以 排序后为61 6

要证明定义的比较规则有效，需要三个条件，自反性，对称性和传递性（<,>=是常规意义的大小关系，大于小于等于是自定义的大小关系）

1. 自反性：显然有aa=aa，所以a等于a
2. 对称性：如果a小于b，则ab小于ba,所以ba>ab,所以b大于a
3. 传递性：如果a小于b，则ab小于ba

class Solution {
    private:
    static bool cmp(const string &a, const string &b) {
        return a + b < b + a;
    }
public:
    string minNumber(vector<int>& nums) {
        vector<string> str;
        string res;
        for (auto num: nums) {
            str.push_back(to_string(num));
        }

        sort(str.begin(), str.end(), cmp);
        for(auto s: str) {
            res += s;
        }
        return res;
    }
};

 code2：

class Solution {
public:
    string PrintMinNumber(vector<int> num)
    {
         if(num.size()==0)
             return "";
        
        sort(num.begin(),num.end(),cmp);
        string res;
        for(int i=0;i<num.size();++i)
            res+=to_string(num[i]);
        return res;
    }
private://写在类内时，要加上static，lexicographical_compare 最后要求的是一个普通函数指针
            //而不是成员函数指针，所以要加static：
    static bool cmp(int a,int b)
    {
        string A(to_string(a));
        A+=to_string(b);
        string B(to_string(b));
        B+=to_string(a);
        
        return A<B;
    }
};