hdu5438 拓扑排序+DFS
解析
对一个有向无环图(Directed Acyclic Graph,简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若<u,v> ∈E(G),则u在线性序列中出现在v之前。
效果如图: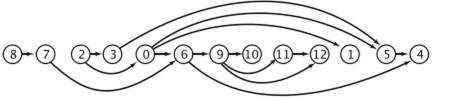
模板
void toposort(int map[MAX][MAX],int indegree[MAX],int n)
{
int i,j,k;
for(i=0;i<n;i++) //遍历n次
{
for(j=0;j<n;j++) //找出入度为0的节点
{
if(indegree[j]==0)
{
indegree[j]--;
cout<<j<<endl;
for(k=0;k<n;k++) //删除与该节点关联的边
{
if(map[j][k]==1)
{
indegree[k]--;
}
}
break;
}
}
}
}
代码
#include <bits/stdc++.h>
using namespace std;
struct Edge{
int u,v,next;
}edge[2000005];
int d[10005],head[10005],power[10005];
bool vis[10005];
int e,m,n,num;
long long sum;
void add(int a,int b)
{
edge[e].u=a;
edge[e].v=b; //建立一个a-b的边
edge[e].next=head[a]; //上一条以a为顶点的边的序号
head[a]=e++; //最后一条以a为顶点的边的序号
}
void dfs(int a)
{
sum += power[a];
num++;
vis[a]=true;
for(int i=head[a];i!=-1;i=edge[i].next)
{
if(!vis[edge[i].v]) dfs(edge[i].v);
}
}
void topo()
{
queue<int>q;
for(int i=1;i<=n;i++)
{
if(d[i]==1) q.push(i);
}
while(!q.empty())
{
int tmp=q.front();
q.pop();
vis[tmp]=true;
d[tmp]--;
for(int i=head[tmp];i!=-1;i=edge[i].next)
{
int v=edge[i].v;
if(d[v]>0) d[v]--;
if(d[v]==1) q.push(v);
}
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int u,v;
e=0;
memset(d,0,sizeof(d));
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&power[i]);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
d[u]++;
d[v]++;
add(u,v);
add(v,u);
}
topo();
long long ans=0;
for(int i=1;i<=n;i++)
{
num=sum=0;
if(d[i]>0&&!vis[i])
{
dfs(i);
if(num%2) ans+=sum;
}
}
printf("%lld\n",ans);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号