Trie 前缀树

一. 介绍

前缀树，能用图解决问题的，就不是问题

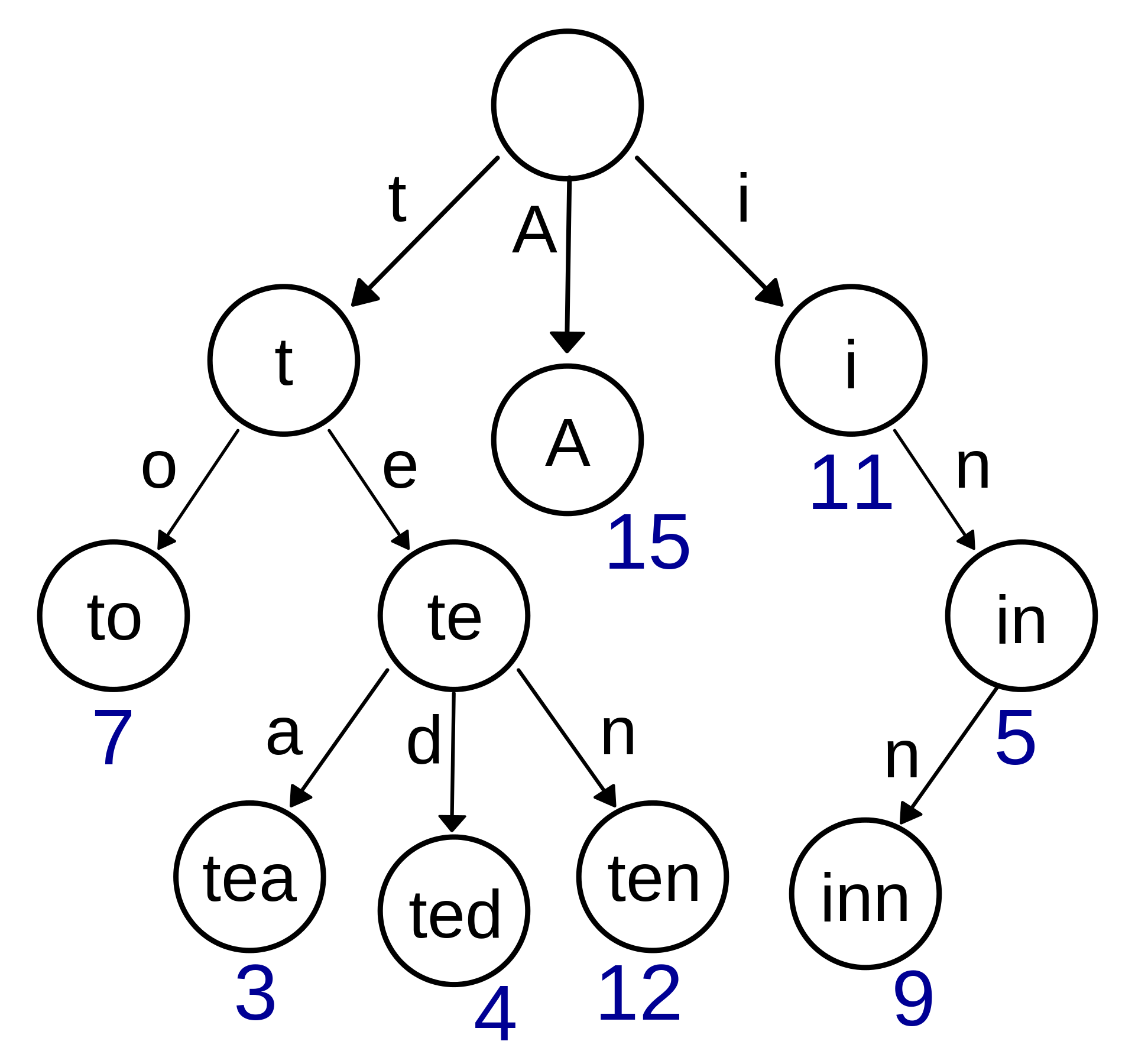
如图所示：
前缀树，可以用来表示一个字符串集合。图中字符串集合的全集S为{t,A,i,to,te,tea,ted,ten,in,inn}。代表字符的为树的边，节点表示整个字符串，一个树就代表字符串集合。
（树中可以有一个标志位，用来表示，该节点下的字符串是否为所定义集合中的字符串。此时，这个树就可以表示为上面S全集的子集。）

原理上很简单，而实现的时候，主要是对树的存储和操作（插入&搜索）。

1. 插入（insert）

对于trie树的插入操作，首先确定当前需要插入的字符串（也就是树边上的值），检查当前节点是否有该边，如果没有，则新建一个；如果有，则更换当前节点为该边连接的孩子节点。继续以上过程，直到字符串中的每个字符都找到了对应位置

2.搜索（search）

搜索与插入相似，不同的是，一旦搜索过程中当前节点的孩子，没有需要的对应字符时，就说明搜索失败，不需要继续搜索了。

二. 实现

对于树，有两种实现方式，一种是使用非连续内存（如链表），一种是连续内存（如数组）。

1. 非连续形式的实现:
   使用了递归实现了插入和搜索。这种实现的方法，时间效率较低，但是节省了空间（由于在匹配子节点时，需要线性查找）

//trie tree
#include <vector>
#include <string>
#include <iostream>

using namespace std;

struct TrieT_node{
    char content;//到该节点的边的值
    bool mark;//标记位
    vector<TrieT_node> childs;//子节点

    TrieT_node(){
        content = '\0';
        mark = false;
    }

    TrieT_node(char c){
        content = c;
        mark = false;
    }
};

struct TrieT{
    TrieT_node root;

    void insert_re(TrieT_node &curr,const string& s,int p){

        if(p >= s.size()){
            curr.mark = true;
            return;
        }

        for (int i = 0; i < curr.childs.size(); i++) {
            if(s[p] == curr.childs[i].content){
                insert_re(curr.childs[i],s,p+1);
                return;
            }
        }
        curr.childs.push_back(TrieT_node(s[p]));
        insert_re(curr.childs[curr.childs.size()-1],s,p+1);
    }

    void insert(const string& s){
        insert_re(root,s,0);
    }

    bool search_re(TrieT_node &curr,const string& s,int p){

        if(p >= s.size()){
            return curr.mark;
        }

        for (int i = 0; i < curr.childs.size(); i++) {
            if(s[p] == curr.childs[i].content){
                return search_re(curr.childs[i],s,p+1);
            }
        }
        return false;
    }

    bool search(const string &s){
        return search_re(root,s,0);
    }
};

int main(){

    TrieT t;
    string s = "abc";
    t.insert(s);
    t.insert("bcf");
    t.insert("abcfg");

    cout<<t.search("abc")<<endl;
    cout<<t.search("saweq")<<endl;

    cout<<t.search("bcf")<<endl;
    cout<<t.search("bcfg")<<endl;
    return 0;
}

2. 以数组形式实现
   前面提到了，由于链表形式会降低时间效率。而我们又知道，实际上字母只有26个，如果使用数字代替每个字母，则查找效率变快。

//trie tree
#include <vector>
#include <string>
#include <iostream>

using namespace std;

struct TrieT_node{
    bool mark;

    TrieT_node* childs[26];

    TrieT_node(){
        for (int i = 0; i < 26; i++) {
            childs[i] = NULL;
        }
        mark = false;
    }


};

struct TrieT{
    TrieT_node root;

    void insert(const string& s){
        TrieT_node* curr = &root;
        for (int i = 0; i < s.size(); i++) {
            int p = s[i]-'a';
            if(curr->childs[p] == NULL){
                curr->childs[p] = new TrieT_node();
                curr = curr->childs[p];
            }else{
                curr = curr->childs[p];
            }
        }
        curr->mark = true;
    }

    bool search(const string &s){
        TrieT_node* curr = &root;
        for (int i = 0; i < s.size(); i++) {
            int p = s[i]-'a';
            if(curr->childs[p] == NULL){
                return false;
            }else{
                curr = curr->childs[p];
            }
        }
        return curr->mark;
    }
};

int main(){

    TrieT t;
    string s = "abc";
    t.insert(s);
    t.insert("bcf");
    t.insert("abcfg");

    cout<<t.search("abc")<<endl;
    cout<<t.search("saweq")<<endl;

    cout<<t.search("bcf")<<endl;
    cout<<t.search("ab")<<endl;
    return 0;
}

附网址：
leetcode自测实现是否正确

三. 更多

大部分情况下，Trie树是要与AC自动机连用，用来是否含有模式字符串集合中的任意一个字符串的。
AC自动机的状态转移，是需要在前缀树的基础上，增加失配指针，具体请看另一篇。