LeetCode腾讯精选50题--最长回文子串

对于此题最长回文子串的问题，我们先写另一个回文子串的题目

  题目：

  

 

 

 分析：

此题要求求的是某个字符串中有多少个回文子串，

两种思路：
1、枚举所有的子串，再对子串进行判断是否为回文子串

2、枚举每个可能的回文中心，然后用两个指针向两边扩展，同时进行判断，不满足条件时，扩展结束

  此题我们用回文中心扩展的方法接，即第二种思路

  在实现的时候，我们需要处理一个问题，即如何有序地枚举所有可能的回文中心，我们需要考虑回文长度是奇数和回文长度是偶数的两种情况。如果回文长度是奇数，那么回文中心是一个字符；如果回文长度是偶数，那么中心是两个字符。当然你可以做两次循环来分别枚举奇数长度和偶数长度的回文，但是我们也可以用一个循环搞定。我们不妨写一组出来观察观察，假设 n = 4，我们可以把可能的回文中心列出来：

 

 

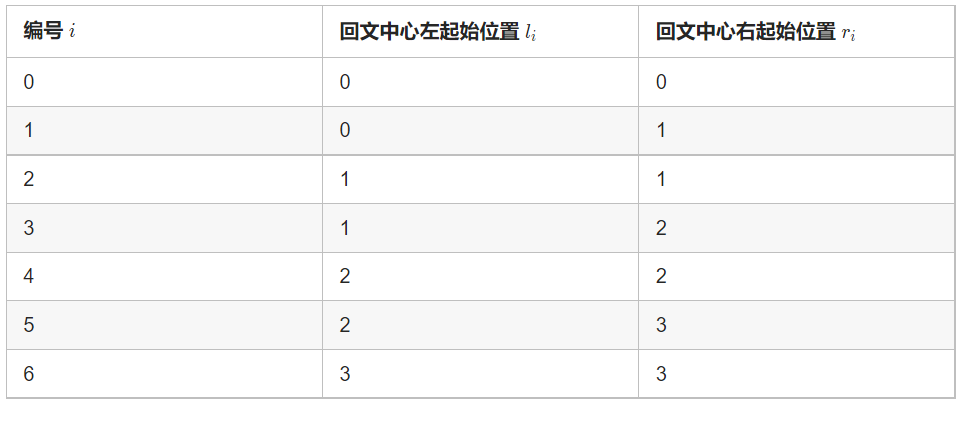
 由此我们可以知道长度为n的字符串会有2n-1组回文中心[Li,Ri],其中Li = i / 2,Ri = i / 2 + i % 2

代码：

class Solution {
    public int countSubstrings(String s) {
        int res = 0;
        int n = s.length();   //字符串长度
        for(int i = 0;i <= 2 * n - 1;i ++){
            int l = i / 2 ,r = i / 2 + i % 2;    //回文中心左右的两个下标
            while(l >= 0 && r < n && s.charAt(l) == s.charAt(r)){   //向两边扩展
                l --;
                r ++;
                res ++;
            }
        }
        return res;
    }
}

解决完这题之后，我们可以进行解决最长回文子串这题

题目：

 

 

 解析：
这题除了用回文中心扩展之外，我们需要再定义一个int型变量，储存最大的回文子串长度，以及两个start和end储存回文子串的左起点和右起点

代码：

class Solution {
    public String longestPalindrome(String s) {
        int n = s.length(),res = 0,res1 = 0;
        int start = 0,end = 0;   //储存最长的回文子串的左起点和右终点
        for(int i = 0;i < 2 * n - 1;i ++){
            int l = i /2,r = i / 2 + i % 2;
            res = 0;
            while(l >= 0 && r < n && s.charAt(l) == s.charAt(r)){
                l --;
                r ++;
            }
            res = r - l - 1;     //当前得到的回文子串长度
            if(res >= res1){     //判断是否是目前最长回文子串，是的话更新信息
                res1 = res;
                start = l + 1;
                end = r - 1;
            }
        }
        
        return s.substring(start,end + 1);    //返回回文子串
    }
}

博主目前只弄懂了中心回文扩展方法，慢慢来。。。