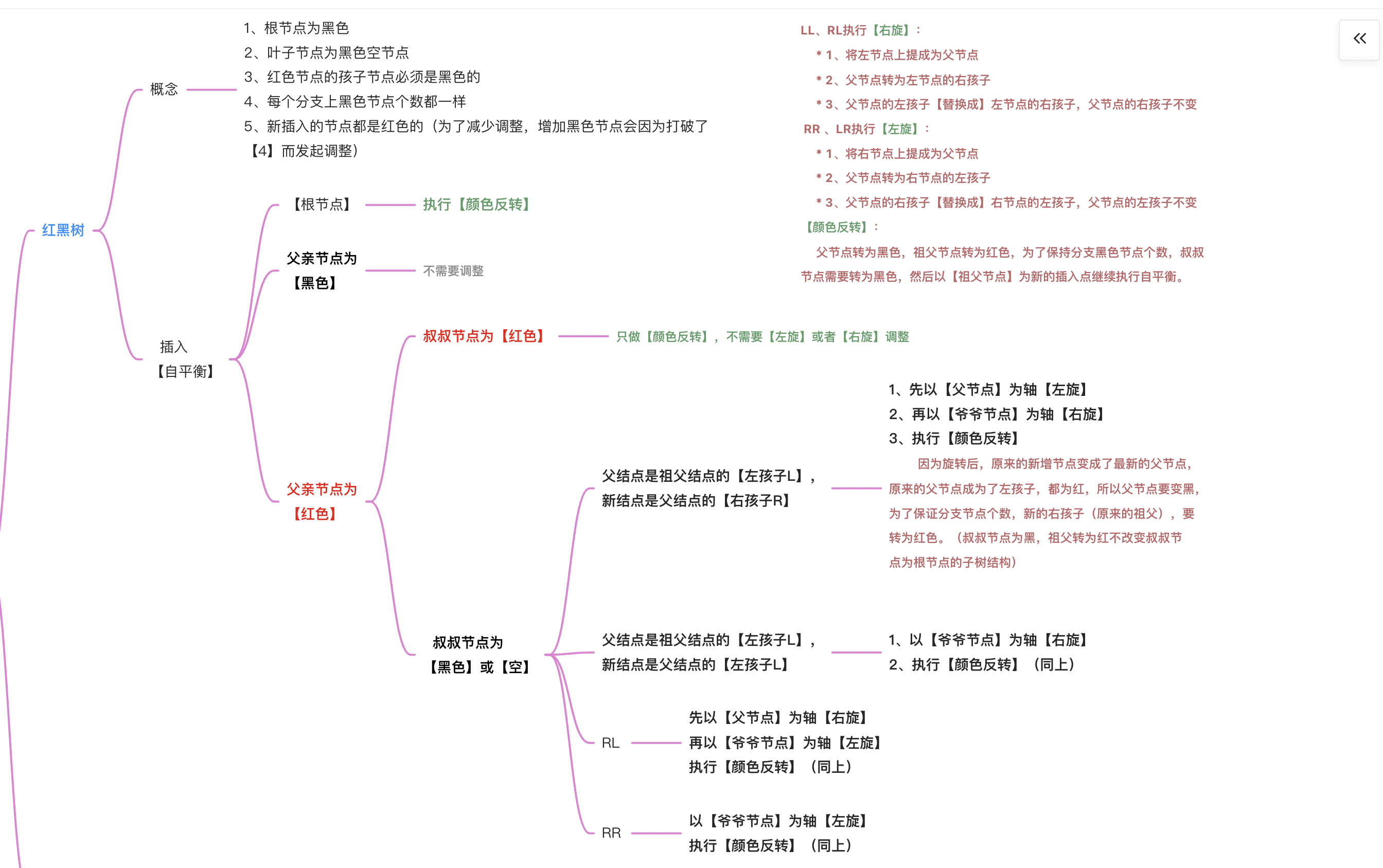
红黑树
package tree.red.black;
/**
* @author: tianhaichao
* @date: 2022/8/29 14:27
* @description: 1、根节点为黑色
* 2、叶子节点为黑色空节点
* 3、红色节点的孩子节点必须是黑色的
* 4、每个分支上黑色节点个数都一样
* 5、新插入的节点都是红色的(为了减少调整,增加黑色节点会因为打破了【4】而发起调整)
*/
public class RBTree {
private static RBTreeNode root;
/**
* @author: tianhaichao
* @date: 2022/9/20 15:55
* @description: 红黑树插入节点,如果打破了红黑树的规则,需要自平衡做调整
* 分以下几种情况:
* 1、父亲节点为【黑色】 ———— 插入红色节点后,没有打破红黑树的规则,【不需要做调整】
* 2、父亲节点为【红色】 ———— 插入节点为红色,需要做【颜色反转】,将父亲节点由红色变为黑色,为了不改变分支上black节点的个数,需要继而向上反转爷爷和祖先节点的颜色
* a、叔叔节点为【红色】 ----- 因为叔叔节点是红色,爷爷节点转变为红色后,叔叔节点必须要转变为黑色。在这个局部的子树中,两个分支上的black节点个数都没有变,所以【不需要左旋或右旋调整】。
* b、叔叔节点为【黑色或空】 ----- 因为叔叔节点是黑色,因为爷爷节点转而为红色,使得叔叔分支上的black节点少了一个,所以需要通过【自平衡】重新回到红黑树
* (叶子结点也是黑色)
* RL: 1、执行【颜色反转】2、先以【父节点】为轴【左旋】3、再以【爷爷节点】为轴【右旋】
* RR: 1、执行【颜色反转】2、以【爷爷节点】为轴【右旋
* LR: 1、执行【颜色反转】2、先以【父节点】为轴【右旋】3、再以【爷爷节点】为轴【左旋】
* LL: 1、执行【颜色反转】2、以【爷爷节点】为轴【左旋】
*/
public static void insert(int data) {
RBTreeNode node = new RBTreeNode(data);
if (root == null) {
// 根节点是黑色的
root = node;
setBlack(node, true);
return;
} else {
// 如果根节点不为空,循环找到叶子节点,执行树插入
RBTreeNode parentNode = root;
RBTreeNode sonNode = null;
// 比较大小分边
if (data >= parentNode.getData()) {
// 遍历右边
sonNode = parentNode.getRight();
} else {
// 遍历左边
sonNode = parentNode.getLeft();
}
// 子节点不为空,继续遍历,直到找到叶子节点
while (sonNode != null) {
parentNode = sonNode;
if (data >= parentNode.getData()) {
// 遍历右边
sonNode = parentNode.getRight();
} else {
// 遍历左边
sonNode = parentNode.getLeft();
}
}
// sonNode == null 是叶子节点
if (data >= parentNode.getData()) {
//插入右节点
parentNode.setRight(node);
node.setPrarent(parentNode);
// 新建都是红色
setBlack(node, false);
} else {
//插入左节点
parentNode.setLeft(node);
node.setPrarent(parentNode);
// 新建都是红色
setBlack(node, false);
}
// 执行自平衡平衡方法
balanceInsert(node);
}
}
public static void setBlack(RBTreeNode node, boolean isBlack) {
if(node == null){
return;
}
if (node != root) {
node.setBlack(isBlack);
} else {
node.setBlack(true);
}
}
/**
* @author: tianhaichao
* @date: 2022/9/20 17:38
* @description:自平衡分以下几种情况: 1、父亲节点为【黑色】 ———— 插入红色节点后,没有打破红黑树的规则,【不需要做调整】
* 2、父亲节点为【红色】 ———— 插入节点为红色,需要做【颜色反转】,将父亲节点由红色变为黑色,为了不改变分支上black节点的个数,需要继而向上反转爷爷和祖先节点的颜色
* a、叔叔节点为【红色】 ----- 因为叔叔节点是红色,爷爷节点转变为红色后,叔叔节点必须要转变为黑色。在这个局部的子树中,两个分支上的black节点个数都没有变,所以【不需要左旋或右旋调整】。
* b、叔叔节点为【黑色或空】 ----- 因为叔叔节点是黑色,因为爷爷节点转而为红色,使得叔叔分支上的black节点少了一个,所以需要通过【自平衡】重新回到红黑树
* (叶子结点也是黑色)
* RL: 1、执行【颜色反转】2、先以【父节点】为轴【左旋】3、再以【爷爷节点】为轴【右旋】
* RR: 1、执行【颜色反转】2、以【爷爷节点】为轴【右旋
* LR: 1、执行【颜色反转】2、先以【父节点】为轴【右旋】3、再以【爷爷节点】为轴【左旋】
* LL: 1、执行【颜色反转】2、以【爷爷节点】为轴【左旋】
*/
public static void balanceInsert(RBTreeNode node) {
//判断father的颜色
RBTreeNode farther = node.getPrarent();
// 父节点是红色的,需要自平衡
while (farther != root && farther != null && farther.isBlack() == false) {
RBTreeNode grandFarther = farther.getPrarent();
// 父亲节点是祖父的右孩子
if (grandFarther.getRight() == farther) {
// 判断叔叔节点颜色 —— red 【颜色反转】不需要【左旋】或【右旋】调整
// 如果叔叔节点不为空,且为红色,反转叔叔节点颜色,祖父节点作为父节点向上传递
if (grandFarther.getLeft() != null && grandFarther.getLeft().isBlack() == false) {
setBlack(farther, true);
setBlack(grandFarther, false);
setBlack(grandFarther.getLeft(), true);
// 此时的改变已经传递到了祖父,祖父变成了红色,相当于新插入
farther = grandFarther.getPrarent();
node= grandFarther;
continue;
} else {
//叔叔节点为黑色或空
if(farther.getLeft()==node){
//RL 右旋 成为RR 然后 以祖父节点左旋
rightRotate(farther);
}
//RR
farther = leftRotate(grandFarther);
setBlack(farther, true);
setBlack(farther.getRight(), false);
setBlack(farther.getLeft(), false);
// 通过调整,father替代祖父的位置变成了黑色,所有分支黑色节点的个数没有变化,整棵树重新满足红黑树规则,跳出循环
break;
}
}
// 父亲节点是祖父的左孩子
if (grandFarther.getLeft() == farther) {
// 判断叔叔节点颜色 —— red 【颜色反转】不需要【左旋】或【右旋】调整
// 如果叔叔节点不为空,且为红色,反转叔叔节点颜色,祖父节点作为父节点向上传递
if (grandFarther.getRight() != null && grandFarther.getRight().isBlack() == false) {
setBlack(farther, true);
setBlack(grandFarther, false);
setBlack(grandFarther.getRight(), true);
// 此时的改变已经传递到了祖父,祖父变成了红色,相当于新插入
farther = grandFarther.getPrarent();
node= grandFarther;
continue;
} else {
//叔叔节点为黑色或空
if(farther.getRight()==node){
//LR 左旋 成为LL 然后 以祖父节点右旋
farther = leftRotate(farther);
}
//LL
farther = rightRotate(grandFarther);
setBlack(farther, true);
setBlack(farther.getRight(), false);
setBlack(farther.getLeft(), false);
}
}
}
}
/**
* @author: tianhaichao
* @date: 2022/8/30 14:44
* @description: node 旋转节点 RR 、LR执行左旋
* 1、将右节点上提成为父节点
* 2、父节点转为右节点的左孩子
* 3、父节点的右孩子【替换成】右节点的左孩子,父节点的左孩子不变
* return 旋转完后的父节点,也就是右孩子【将右节点上提成为父节点】
*/
public static RBTreeNode leftRotate(RBTreeNode node) {
RBTreeNode right = node.getRight();
RBTreeNode father = node;
// 如果右节点存在左孩子,父节点的右孩子【替换成】右节点的左孩子
father.setRight(right.getLeft());
// 将右节点上提成为父节点 变成祖父的孩子
if (father.getPrarent() == null || father == root) {
root = right;
} else if (father.getPrarent().getLeft() == father) {
father.getPrarent().setLeft(right);
} else {
// 如果旋转节点是父节点的右节点
father.getPrarent().setRight(right);
}
right.setPrarent(father.getPrarent());
// 父节点转为右节点的左孩子
right.setLeft(father);
father.setPrarent(right);
return right;
}
/**
* @return 旋转之后的父节点,也就是左孩子【将左节点上提成为父节点】
* @author: tianhaichao
* @date: 2022/9/20 18:31
* @description: LL或RL执行右旋
* 执行右旋,
* 1、将左节点上提成为父节点
* 2、父节点转为左节点的右孩子
* 3、父节点的左孩子【替换成】左节点的右孩子,父节点的右孩子不变
*/
public static RBTreeNode rightRotate(RBTreeNode node) {
RBTreeNode left = node.getLeft();
RBTreeNode father = node;
// 父节点的左孩子【替换成】左节点的右孩子,父节点的右孩子不变
father.setLeft(left.getRight());
//将左节点上提成为父节点
if (father.getPrarent() == null || father == root) {
root = left;
} else if (father.getPrarent().getRight() == father) {
father.getPrarent().setRight(left);
} else {
father.getPrarent().setLeft(left);
}
left.setPrarent(father.getPrarent());
// 父节点转为左节点的右孩子
father.setPrarent(left);
left.setRight(father);
return left;
}
public static void main(String[] args) {
int[] array = new int[]{10, 3, 5, 2, 5, 6, 4, 12, 15, 16, 17, 18};
for (int i : array) {
RBTree.insert(i);
preTraversal(root);
System.out.println("----" + i);
}
System.out.println("==========================");
//排序输出
midTraversal(root);
}
/**
* @author: tianhaichao
* @date: 2022/9/20 15:10
* @description:中序遍历
*/
public static void midTraversal(RBTreeNode node) {
if (node == null) {
return;
}
midTraversal(node.getLeft());
System.out.print(node.getData() +" ");
midTraversal(node.getRight());
}
/**
* @author: tianhaichao
* @date: 2022/9/20 15:10
* @description:中序遍历
*/
public static void preTraversal(RBTreeNode node) {
if (node == null) {
return;
}
int left = node.getLeft()!=null?node.getLeft().getData():0;
int right = node.getRight() != null?node.getRight().getData():0;
System.out.print(node.getData() +"【"+node.isBlack()+left+" "+right+"】"+ " ");
preTraversal(node.getLeft());
preTraversal(node.getRight());
}
}
package tree.red.black;
/**
* @author: tianhaichao
* @date: 2022/8/29 14:20
* @description: 红黑树节点
*/
public class RBTreeNode {
private int data;
private RBTreeNode prarent;
private RBTreeNode left;
private RBTreeNode right;
// get set方法省略……
}

验证工具:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号