一本通1508：Easy SSSP

题目传送门

1508：Easy SSSP

【题目描述】

输入数据给出一个有 N 个节点，M 条边的带权有向图。要求你写一个程序，判断这个有向图中是否存在负权回路。如果从一个点沿着某条路径出发，又回到了自己，而且所经过的边上的权和小于 0，就说这条路是一个负权回路。

如果存在负权回路，只输出一行 −1；如果不存在负权回路，再求出一个点S到每个点的最短路的长度。约定：S 到 S 的距离为 0，如果 S 与这个点不连通，则输出 NoPath。

【输入】

第一行三个正整数，分别为点数 N，边数 M，源点 S；

以下 M 行，每行三个整数 a,b,c，表示点 a,b 之间连有一条边，权值为 c。

【输出】

如果存在负权环，只输出一行 −1，否则按以下格式输出：

共 N 行，第 i 行描述 S 点到点 i 的最短路：

如果 S 与 i 不连通，输出 NoPath；

如果 i=S，输出 0。

其他情况输出 S 到 i 的最短路的长度。

【输入样例】

6 8 1
1 3 4
1 2 6
3 4 -7
6 4 2
2 4 5
3 6 3
4 5 1
3 5 4

【输出样例】

0
6
4
-3
-2
7

【提示】

数据范围：

对于全部数据，2≤N≤1000,1≤M≤10⁵,1≤a,b,S≤N,∣c∣≤10⁶。

---

这道题看到n最大为1000,Floyed是不行的.Dijkstra有些大佬说能写,在这里我就用SPFA.

对于SPFA来说,它判定负权回路的方法就是开一个计数的数组.只要这个元素入队的次数大于了n次,那么说明这里就存在负权环.

那就写一个裸的SPFA吧.

那么恭喜你,一本通上第3个点你会WA的.

因为负权环可能没有和起点连在一起!!!

如下图所示:

 

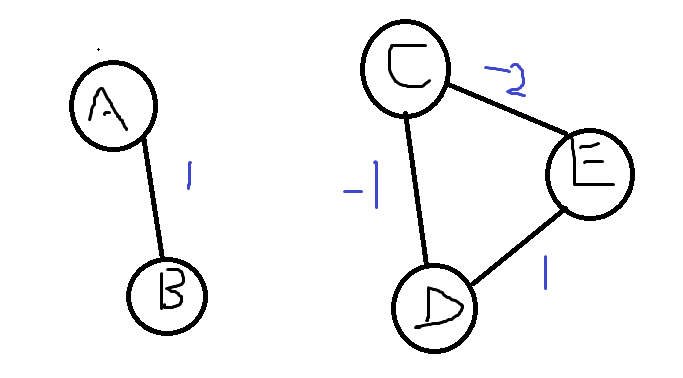
这是一个非连通图.我们假设起点为A点,那么右边的CDE三点构成了一个负权环.

但是我们以A点为起点跑SPFA的话就无法判断CDE三点的情况.

正确的输出应为-1,然而我们的输出会是0 1 NoPath Nopath Nopath.

那么应该怎么办呢?

---

 

思考一下,如果我们将没有连通的点构成的图再跑一遍SPFA不就行了?

那么我们就可以开一个布尔数组,如果这个点入过队,就把它标记为true.跑了一遍SPFA之后返回枚举没有入过队的点再跑一遍就行啦.

Tip:要开long long!!!

代码在下面:

#include<bits/stdc++.h>
#define inf 0x6fffffff
#define ll long long
#define maxn 1005
using namespace std;
struct node{
    ll v,w,nxt;
}edge[maxn*100];
ll n,m,cnt[maxn],dis[maxn],k=1,s,head[maxn],ans[maxn];
bool vis[maxn],done[maxn];
inline void adde(ll u,ll v,ll w)
{
    edge[k].v=v;
    edge[k].w=w;
    edge[k].nxt=head[u];
    head[u]=k++;
}
deque<ll> q;
inline bool SPFA(ll s)
{
    for(int i=1;i<=n;i++) cnt[i]=0; 
    if(!q.empty()) q.pop_front();
    for(int i=1;i<maxn;i++) dis[i]=inf;
    dis[s]=0;
    q.push_back(s);
    while(!q.empty())
    {
        ll u=q.front();q.pop_front();
        vis[u]=0;
        for(int i=head[u];i;i=edge[i].nxt)
        {
            ll v=edge[i].v;
            if(dis[v]>dis[u]+edge[i].w)
            {
                dis[v]=dis[u]+edge[i].w;
                if(!vis[v])
                {
                    done[v]=1;
                    cnt[v]++;
                    if(cnt[v]>n) return 0;
                    if(q.empty()) q.push_back(v);
                    else
                    {
                        if(dis[v]<dis[q.front()]) q.push_front(v);
                        else q.push_back(v);
                    }
                    vis[v]=1;
                }
            }
        }
    }
    return 1;
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&s);
    for(int i=1;i<=m;i++)
    {
        ll t1,t2,t3;
        scanf("%lld%lld%lld",&t1,&t2,&t3);
        adde(t1,t2,t3);
    }
    int haha=SPFA(s);
    if(!haha) 
    {
        printf("-1");
        return 0;
    }
    for(int i=1;i<=n;i++) ans[i]=dis[i];
    for(int i=1;i<=n;i++)
    {
        if(!done[i])
        {
            haha=SPFA(i);
            if(!haha)
            {
                printf("-1");
                return 0;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(ans[i]<inf) printf("%lld\n",ans[i]);
        else printf("NoPath\n");
    }
    return 0;
}

这道题坑点很多,一定要小心