Day 2:数学部分 feecle6418讲课记录

上午：线性代数/线性变换

前置芝士：

代数（学）：

代数定义：用抽象的符号表示数。

代数学定义：不拘泥于具体的数集，得到对于满足一类抽象的性质的数集（甚至其它物品的集合）都成立的结论。

满足特定性质的数集通常称为“代数结构”，例子：群，环，域。

1. 半群：集合 𝑆 以及满足结合律的运算。相当于有\(+ \times ()\)的运算符。
   因为结合律，所以显然可以使用线段树维护信息的和。可以使用快速幂维护多次运算的结果。
2. 群：集合 𝑆 以及满足结合律、可逆的运算。相比半群而言，群相当多了\(-\) 和 \(\div\)的操作，使它可以使用树状数组，前缀和维护信息的和。
3. 域：集合 𝑆 以及满足结合律、可逆的加法，满足结合律、分配律、可逆的乘法。在模 𝑝 意义下，可以像数一样进行加减乘除操作，相比群而言，又多了拆解括号的能力。

线性代数：

即“线性”的代数。

“代数”：有若干个（\(𝑛\) 个）变元 \(𝑥_1,…,𝑥_𝑛\)。

“线性”：只有一次项。（没有零次项！）

把一列数称为一个“向量”。

一个向量到另一个向量的过程，称为“变换”。

如果“变换”得到的新向量的每一项都是原来的向量的变元的一次式（没有常数！）则称其为“线性变换”。

矩阵

什么向量没听懂啊？

其中矩阵 C 中的第 i 行第 j 列元素可以表示为：

\[C_{i,j}=\sum_{k=1}^mA_{i,k}B_{k,j} \]

C矩阵的第 \(i\) 行第 \(j\) 列的数，就是由矩阵 \(A\) 第 \(i\) 行 \(M\) 个数与矩阵 \(B\) 第 \(j\) 列 \(M\) 个数分别 相乘再相加 得到的。（A第i个行向量与B第j个列向量内积）

好吧先谈谈我的理解

\[\begin{bmatrix} {\color{green} 1 } & {\color{green} 2} \\ 3 & 4 \end{bmatrix} \times \begin{bmatrix} {\color{red} 1 } & 2 \\ {\color{red} 3} & 4 \end{bmatrix} = \begin{bmatrix} {\color{yellow} 1 } & 2 \\ 3 & 4 \end{bmatrix} \]

左行右列嘛，第三矩阵的（1，1）的位置上的数就是由第一矩阵第一行（行向量）与由第二矩阵第一列（列向量）做内积。

行向量是递推公式，列向量是给的条件值，根据两者推出当前位置的答案，通过重复的几次运算，就可以得到最终答案。

矩阵描述了线性变换。

如果在群，环，域上，你就将重复的几次线性变换运算压缩成快速幂形式，最后再与条件相乘。

矩阵乘法具有结合律，通常不具有交换律。

“矩阵快速幂”：利用矩阵乘法 / 线性变换的结合律性质，指导“计算固定线性变换的 𝑘 次幂”这一实践。

矩阵乘法可以看作线性变换的复合，但是没搞懂啊！

试图使用矩阵快速幂时：

1. 将问题合理分层，使得每一层转移都是相同的线性变换。
2. 经典技巧：对于 \(𝑛^𝑘,𝑘^𝑛\) 的处理。

\(𝑛^𝑘\)的处理通过二项式定理

\[(1+𝑥)^𝑘=\sum_{i=1}^k𝐶(𝑘,𝑖) 𝑥^𝑖 \]

的形式将\(1\sim k\)的 \(x^i\) 全保存下来，一层一层的处理上来（所以\(k\)不会太大）

\(k^n\)有点幽默，直接由\(k^{n-1}\)转过来就好了。

问题越复杂，为了把递推式写成线性变换，向量的长度就越长。

初等变换:

1. 交换两行。
2. 把一行乘以 𝑘（不等于 0）。
3. 把一行乘以 𝑘 加到另一行上去。

这些变换都可以用矩阵来描述！

一列一列地进行初等行变换，可以把任意矩阵 𝐴 变为“简化阶梯型矩阵”𝐵：每一列至多只有一个 1 的矩阵。

行列式：

滚啊！！！

线性组合/空间/相关.......

给每行一个系数，每个向量乘上系数求和，得到一个新向量。这个新向量就是原向量组的一个线性组合。

\(𝑥_𝑖\) 线性相关，等价于 （∃表示至少有一个）\(∃𝑥_𝑖\)，能被 \(𝑥_1,…,𝑥_(𝑖−1),𝑥_(𝑖+1),…,𝑥_𝑛\) 线性表出。

如果 \(∃𝑎_1,…,𝑎_𝑛\) 非全 0，\(∑𝑎_𝑖 𝑥_𝑖=0\)，就说 \(𝑥_𝑖\) 线性相关。(\(a_i\)的含义是给每个向量乘上的系数)

若 \(𝑠𝑝𝑎𝑛(𝑦_1,…,𝑦_𝑚 )=𝑆\)，且(∀为任意一个) \(∀𝑘<𝑚,∀𝑢_𝑖,𝑠𝑝𝑎𝑛(𝑢_1,…,𝑢_𝑘 )≠𝑆\)，则称 \((𝑦_1,…,𝑦_𝑚)\) 的“维数”或者“秩”为 \(𝑚\)（向量组的极大线性无关组的大小为向量组的秩，因为\(m+1\) 个 \(m\) 维向量必定线性相关,所以秩是\(m\)），且 \(𝑦_1,…,𝑦_𝑚\) 是 \(𝑆\) 的一组基。

定理：若 \(𝑦_𝑖\) 不线性相关，则 \(𝑦_1,…,𝑦_𝑚\) 是 \(𝑆\) 的一组基。

找基，其实是找一组极大线性无关组。(算了，算法竞赛上讲的也好，太累了，结束。)

下午：概率+计数

期望的线性性和独立性

定理：\(𝐸[𝑋+𝑌]=𝐸[𝑋]+𝐸[𝑌]\)。

定理：若 \(𝑋,𝑌\) 相互独立，则 \(𝐸[𝑋𝑌]=𝐸[𝑋]𝐸[𝑌]\)。

组合数

范德蒙德卷积

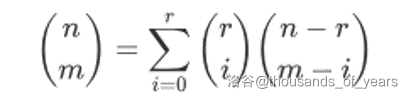
组合意义：在某处划成两半，这里假设\(r<mid\)，我们枚举左边取得\(i\)个数的方法数乘上右边取得\(m-i\)个数的方法数求和就是总方法数。

上指标求和

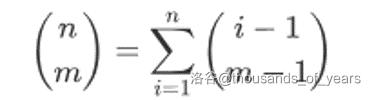
组合意义：我们定义取的数是当前取的数中编号（下标）最大值的贡献，这样可以算的不重不漏。枚举编号（下标）最大值为\(i\)，因为\(i\)必选，所以还要在小于它的编号\(i-1\)中选\(m-1\)个，累加方法数即可。

二项式定理

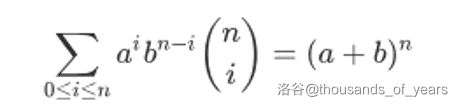
众所周知，不会的可以看算法竞赛。

组合技巧

PPT：足够好。

容斥原理和二项式反演

\[𝑓(𝑛)=\sum_{𝑖≤𝑛}𝑔(𝑖)⋅𝐶(𝑛,𝑖)→𝑔(𝑛)=\sum_{𝑖≤𝑛}𝑓(𝑖)⋅(−1)^{𝑛−𝑖} 𝐶(𝑛,𝑖) \]

\[𝑓(𝑛)=\sum_{𝑖≤𝑛}𝑔(𝑖)⋅𝐶(𝑖,𝑛)→𝑔(𝑛)=\sum_{𝑖≤𝑛}𝑓(𝑖)⋅(−1)^{𝑖−𝑛} 𝐶(𝑖,𝑛) \]

PPT。

生成函数

PPT。

后记：

发现忘了补dp套路：

1. 关于算贡献

例题：CF1542D

大体题意：给你一串维护一个小根堆操作序列，求其所有操作子序列最后剩下的数之和（如果当前堆内无值则当前删除操作无效）

根据所示图上的思路，我们转化为每个+ x的操作一共做了多少次贡献。

先枚举p为哪一个+ x的操作产生贡献，然后设\(dp_{i,j}\)为当前状态到第 \(i\) 位之前，有 \(j\) 个小于它的数的方案数，细节大分讨就做完了。

2. 拆式子 基本原理：如果要求 \(∑(𝑎_𝑖+𝑏_𝑖 )𝑓(𝑖)\)，试图分开求 \(∑𝑎_𝑖 𝑓(𝑖) 和 ∑𝑏_𝑖 𝑓(𝑖)\)。

困难题举例：P4458

给定一个序列 \(𝑎[1..𝑛]\)，\(𝑞\) 次操作，支持：区间加，给一个区间，求出其所有子区间的和的和（对 998244353 取模）

题解
好吧，挺简单吗？（就是要用手算有点史）

3. 带着系数 DP(?没看懂)

原理：假设要求 \(∑∏𝑎_𝑖\)，其中 \(𝑖\) 表示第 \(𝑖\) 个阶段，则把 \(dp\) 状态设为“当前的”\(∑∏𝑎_𝑖\)。

4. 乘积的组合意义(记得来补)

基本原理：$$ 堆物品，每堆大小为 \(𝑎_𝑖\)，每堆物品里选一个的方案数为 \(∏𝑎_𝑖\)。

有时，遇见“求 \(∏𝑎_𝑖\) 之和”或者类似的，可以试图将乘积看成“是否已选”来计算。

同理，求 \(𝐸[𝑥^2]\) 可以看作从 𝑥 中选两个的方案数的期望。

5. 分类确保唯一性（记得来补）

基本原理：假设我们要算 𝑆 中元素的和，我们可以进行试图将所有元素分类，每种元素恰好在一类中，来保证不重不漏。