8.6培训 D1
今天是赵和旭老师讲课(也是 zhx)
动态规划
利用最优化原理把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解(有点像分治?)
更具体的,假设我们可以计算出小问题的最优解,那么我们凭借此可以推出大问题的最优解,进而我们又可以推出更大问题的最优解。(要满足最优子结构)
(从小问题答案推到大问题的答案)
而最小的问题也就是边界情况我们可以直接计算出答案来。
动态规划的状态
动态规划过程中,需要有状态表示和最优化值(方案值)。
状态表示:是对当前子问题的解的局面集合的一种(充分的)描述。
最优化值:则是对应的状态集合下的最优化信息(方案值),我们最终能通过其直接或间接得到答案。
怎么计算动态规划的时间复杂度?
一般简单动态规划时间复杂度 == 状态数×状态转移复杂度。
同时也就引出了 dp 的两种优化时间的方法
1:减少状态的维数。
2:加速状态转移,例如数据结构优化或者分析性质。
一些例题
最长上升子序列(Longest Increasing Subsequence) LIS
给出一个长度为 n 的数列 a[1..n], 求这个数列的最长上升子序列。
就是给你一个序列,请你在其中求出一段不断严格上升的子序列,子序列是不一定要求连续的。
2, 3, 4, 7 和 2, 3, 4, 6 是序列 2 5 3 4 1 7 6 的两种选取方案。最长上升子序列的长度就是 4。
N<=1000
考虑对于一个上升子序列,他的前一位也是一个最长上升子序列,所以我们发现问题变小了
这是一道最为经典的完全用动态规划来解决的问题。
设 dp[i] 为以 a[i] 为末尾的最长上升子序列的长度。
最后的答案就是我枚举一下最长上升子序列的结束位置,然后取一个 dp[i] 最大值即可。
问题是如何求这个数组?
那我们回过头来想一想最开始说的动态规划的基本思想,从小的问题推出大的问题。
贴一下代码吧
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a[100010], n, dp[100010], ans = 0;
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
{
scanf("%d", &a[i]);
dp[i] = 1;
}
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= i; ++j)
{
if (a[j] < a[i]) //当i之前的数比i小时更新dp[i]
dp[i] = max(dp[i], dp[j] + 1);
}
for (int i = 1; i <= n; ++i)
ans = max(ans, dp[i]);
printf("%d", ans);
return 0;
}
复杂度是 n^2 的
在这个问题的分析中,突破口?
1:设计出了 dp[1..n] 这个可以储存以 i 结尾的子序列中最优的答案,这个状态表示。
2:通过分析问题成功能将当前状态的最优值能过由之前状态转移出来。
dp[i] = max {
dp[j] | a[j] < a[i] / & /& j<i } +1;
再来一个
乘积最大
今年是国际数学联盟确定的“2000——世界数学年”,又恰逢我国著名数学家华罗庚先生诞辰90周年。在华罗庚先生的家乡江苏金坛,组织了一场别开生面的数学智力竞赛的活动,你的一个好朋友XZ也有幸得以参加。活动中,主持人给所有参加活动的选手出了这样一道题目:
设有一个长度为N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积最大。
同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子:
有一个数字串:312, 当N=3,K=1时会有以下两种分法:
1)3*12=36
2)31*2=62
这时,符合题目要求的结果是:31*2=62。
现在,请你帮助你的好朋友XZ设计一个程序,求得正确的答案。
有一个数字串:312,当 N=3,K=1 时会有以下两种分法:
- 3*12=36
- 31*2=62
这时,符合题目要求的结果是:31*2=62
现在,请你帮助你的好朋友 XZ 设计一个程序,求得正确的答案。
N,K(6≤N≤80,1≤K≤50)
题解
用 f[i][a) 表示前 i 位数包含 a 个乘号所能达到的最大乘积,我们只需要枚举上一个乘号所在的位置即可。
将 j 从 a 到 i - 1 进行一次枚举,表示前 j 位中含有 a-1 个乘号,且最后一个乘号的位置在 j 处。那么当最后一个乘号在 j 处时最大值为前 j 位中含有 a - 1 个乘号的最大值乘上 j 处之后到 i 的数字。
这里注意要预处理出来第k+1到第i项的值
因此得出了状态转移方程 f[i][a) = max(f[i][a) , f[j][a-1) * cut(j + 1, i))
——(cut(b + 1, i) 表示 b + 1 到 i 位数字)
然后再写个高精度即可。
#include <bits/stdc++.h>
using namespace std;
int n, m, ch[11], num[11][11], f[11][11];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
scanf("%1d", ch + i);
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j++)
num[i][j] = num[i][j - 1] * 10 + ch[j]; //进行出预处理
for (int i = 1; i <= n; i++)
f[i][0] = num[1][i]; //初始化的部分
for (int k = 1; k <= m; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j < i; j++)
f[i][k] = max(f[i][k], f[j][k - 1] * num[j + 1][i]); //k个乘号有k-1个乘号推导出来
cout << f[n][m] << endl;
return 0;
}
前面几个例题真的是尽力写代码了
bzoj4247: 挂饰
N 个装在手机上的挂饰。挂饰附有可以挂其他挂件的挂钩。
每个挂件要么直接挂在手机上,要么挂在其他挂件的挂钩上。直接挂在手机上的挂件最多有 1 个。此外,每个挂件有一个安装时会获得的喜悦值,用一个整数来表示,可能为负。
想要选出一些挂饰挂在一起,最大化所有挂饰的喜悦值之和。
1<=N<=20000<=Ai<=N(1<=i<=N) 表示挂勾的数量
-106<=Bi<=106(1<=i<=N) 表示喜悦值。
对于挂钩数量降序排列,为什么??
因为如果想要保证所有的挂钩都被挂上,那么如果有有一个物品有 0 个挂钩,那么他后面所有的挂钩都没法挂
然后设dp[i][j]前i个挂饰,剩余j个挂钩的最大喜悦值是多少即可。
转移枚举下一个挂饰是否挂,注意dp[i][0]不能转移。
LIS 相关问题
洛谷 P1233 木棍加工
一堆木头棍子共有 n 根,每根棍子的长度和宽度都是已知的。棍子可以被一台机器一个接一个地加工。机器处理一根棍子之前需要准备时间。准备时间是这样定义的:
第一根棍子的准备时间为 1 分钟;
如果刚处理完长度为 L,宽度为 W 的棍子,那么如果下一个棍子长度为 Li,宽度为 Wi,并且满足 L>=Li,W>=Wi,这个棍子就不需要准备时间,否则需要 1 分钟的准备时间;
计算处理完 n 根棍子所需要的最短准备时间。比如,你有 5 根棍子,长度和宽度分别为 (4, 9),(5, 2),(2, 1),(3, 5),(1, 4),最短准备时间为 2(按 (4, 9)、(3, 5)、(1, 4)、(5, 2)、(2, 1) 的次序进行加工)。
N<=5000
这是一个二维的最长不下降子序列
我们对于 l(长度)进行排序, 那么问题转化成了如何用最小的不下降子序列数量来覆盖整个集合
按w从大到小排序,w相同的l从大到小排序,我们对于1分钟能处理的一串棍子实际上就是一个l的不上升子序列,我们这里是求一个不上升子序列覆盖数。
不上升子序列覆盖数=最长上升子序列长度。
(严格证明参考:dilworth定理)
所以其实就是求一个最长上升子序列即可。
其实和导弹拦截很像
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
inline int read()
{
int res = 0;
char ch = getchar(), last = ' ';
while (ch < '0' || ch > '9')
last = ch, ch = getchar();
while (ch >= '0' && ch <= '9')
res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();
if (last == '-')
res = -res;
return res;
}
struct tree
{
int l, w;
} t[5010];
bool cmp(tree a, tree b)
{
if (a.l == b.l)
return a.w > b.w;
return a.l > b.l;
}
int n, ans = 0, dp[5010] = {0};
int main()
{
n = read();
for (int i = 1; i <= n; ++i)
t[i].l = read(), t[i].w = read();
sort(t + 1, t + n + 1, cmp);
dp[1] = 1;
for (int i = 2; i <= n; ++i)
{
for (int j = 0; j <= i; ++j)
if (t[j].w < t[i].w) //出现不合法情况
dp[i] = max(dp[i], dp[j] + 1);
ans = max(ans, dp[i]);
}
printf("%d", ans);
return 0;
}
洛谷 P1091 合唱队形
N 位同学站成一排,音乐老师要请其中的 ( N−K ) 位同学出列,使得剩下的 K 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 K 位同学从左到右依次编号为 1, 2, …,他们的身高分别为 T_1, T_2, …, T_K
则他们的身高满足 T1<T2<T3..
你的任务是,已知所有 N 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
n<=100000
题解
我们设f[i]表示以i结尾的最长上升子序列长度。
我们设g[i]表示以i开头的最长下降子序列长度。
然后我们枚举哪一个为中心的最高点,f[i]+g[i]-1取最大值即可。
(好像数据结构啊hhhh,有点预处理在里面)
对 DP 优化的初探
LIS 的加强版
我们设 h[k] 表示 dp[j]==k 的所有 j 当中的最小的 a[j],就是说长度为 k 的最长上升序列,最后一个元素的最小值是多少,因为最后一个元素越小,肯定后面更容易再加上一个元素了。
感觉出来这个东西是单调不下降的
可以用反证法来进行证明
所以如果要求这个答案我们就可以二分了
二分
所以时间复杂度是O(nlogn),代码的话我直接把我木材加工贴过来了,挺像的
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
inline int read()
{
int res = 0;
char ch = getchar(), last = ' ';
while (ch < '0' || ch > '9')
last = ch, ch = getchar();
while (ch >= '0' && ch <= '9')
res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();
if (last == '-')
res = -res;
return res;
}
struct tree
{
int l, w;
} t[5010];
bool cmp(tree a, tree b)
{
if (a.l == b.l)
return a.w > b.w;
return a.l > b.l;
}
int n, ans = 0, dp[5010] = {0};
int main()
{
n = read();
for (int i = 1; i <= n; ++i)
t[i].l = read(), t[i].w = read();
sort(t + 1, t + n + 1, cmp);
dp[1] = 1;
for (int i = 2; i <= n; ++i)
{
for (int j = 0; j <= i; ++j)
if (t[j].w < t[i].w) //出现不合法情况
dp[i] = max(dp[i], dp[j] + 1);
ans = max(ans, dp[i]);
}
printf("%d", ans);
return 0;
}
二分的话还可以用lower_bound和upper_bound
数据结构优化
数据结构不需要什么灵巧的闪光就是套路。
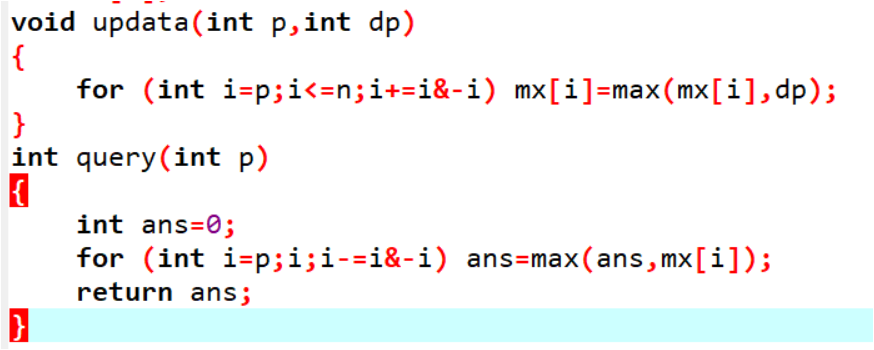
状态转移:dp[i]=max{ dp[j] | a[j]<a[i] && j<i } +1 ;
我们把a[j]看成坐标,dp[j]看成权值,这就是每次求坐标小于等于某个值的权值最大值,然后每算完一个单点修改即可。
线段树能做,但是大材小用了,其实树状数组就可以解决。
LCS相关问题(最长公共子序列)
最长公共子序列
给定两个字符串S和T,长度分别为n和m,求解这两个字符串的最长公共子序列(Longest Common Sequence)。
比如字符串S:BDCABA;字符串T:ABCBDAB
则这两个字符串的最长公共子序列长度为4,最长公共子序列是:BCBA。
n, m<=1000
题解
我们设dp[i][j]表示,S串的第i个前缀和T串的第j个前缀的最长公共子序列。
分情况:
如果S[i]==T[j],dp[i][j]=dp[i-1][j-1]+1;
如果S[i]!=T[j],dp[i][j]=dp[i][j - 1] + dp[i-1][j] - dp[i-1]j-1
最后答案就是dp[n][m]
对于dp[i][j]:
如果,两个串最后一个位置相同,这两个位置一定在公共子序列中。
那么我们只需要求出S的i-1前缀和T的j-1前缀的最长上升子序列就可以了,而这个就是把问题化小。
如果最后一个位置不相同,那么两个位置一定不能匹配,所以肯定是另外两种情况选最大的。
最长公共上升子序列 LCIS ——分析性质优化状态转移
我们设dp[i][j]表示A前i个位置和B前j个位置所能产生的最长公共上升子序列的长度。其中强制A[i]==B[j],也就是最后这个位置是匹配的。若是A[i]!=B[j]则对应函数值为0。
原本是一维的,我们这里用二维来做
所以状态数就是 n^2, 转移也是 n^2,那么就是 n^4
如何变成 n^3?
比如我们算dp[4][5], 那我们算3,4这一块的就行了,当算dp[4][6],也就是有一个维度增加了,所以我们只需要算dp[3][4]和dp[1-3][5],那么就是少了一个维度,所以复杂度变成了n^3
还能在优化,就是说我某一个维度每一次增加一个数,我还得算一次 o(n)对吧,那么我们就用一个类似于树状数组的辅助数组来进行 O(1)
我们从1到n枚举i计算dp值, 在枚举i的过程中维护
f[k] = max {
dp[1…(i - 1)][k]
}
对于维护 f 数组,因为每一次维度 ++,都只需要用当前 f 和加的这个数取一个 max
就可以了
show you the code

DP 与容斥初步
非常非常简单的证明
考虑二项式定理
给定一些条件,问全部满足的对象的个数。
答案 = 所有对象 - 至少不满足其中一个的 + 至少不满足其中两个的 - 至少不满足其中三个的 +……
证明:考虑对于一个恰好不满足 k 个的的对象,被计算了几次。
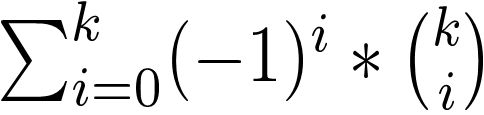
显然只有当 k=0 时,这个对象才会被算进答案,所以我们就证明了上面这个容斥方法的正确性。
Bzoj3782 简化版(网格路径计数 强化版)
从 n*m 网格图的左下角走到右上角 (n, m<=10^8), 有 t 个坐标不能经过 (t<=200), 只能向上向右走,问有多少种不同的走法,对 10^9+7 取模。
Dp 是处理计数问题应该非常常用的方法,而计数问题又常常与容斥原理相结合。
考虑 t=1 的情况,我们只需要把总的路径条数减去经过那个障碍点的路径条数就可以了。走法 =”左下角到障碍点的走法”*”障碍点到右上角的做法”
t=2 时,设两个障碍点为 A, B, ”总的路径条数”-“经过 A 的路径条数”-“经过 B 的路径条数”算出来的答案可能偏小,如果 A, B 可以同时经过,那么最终答案要加上”同时经过 A, B 的路径条数”。
那么这道题就可以用容斥来做。随意填-至少遇到一个障碍的方案数+至少遇到两个障碍的方案数-至少遇见三个障碍的方案数………………
给障碍点从左到右从下到上排个序, 记f[i][j]表示走到了第i个障碍点且包括第i个点在内强制经过了j个障碍点的路径条数(除此之外也可能有经过的), 枚举上一个经过的障碍点即可。
转移的时候乘上一个组合数表示从k到i的走法数目
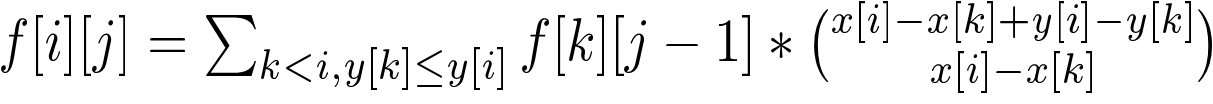

记忆化搜索
网格图路径计数
给出一个n*m的网格,每次只能向右或者向下走,求从(1, 1)走到(n, m)的方案数,其中有些位置是不能走的。
n, m<=1000
我们从另一个角度来思考这个问题。
我们用搜索算法来计算答案,先看看没有障碍的情况,有障碍只改一点。

然而搜索的时间复杂度是指数级的。
观察一下:这是有些重复计算的。
我们发现在这个dfs的过程中,dfs出来的值只与带入参数,也就是(x, y)有关,而不同的(x, y)有N*M个,而我们之前搜索的问题在于有大量的重复计算,多次调用同一个(x, y),每次都从新计算。
有一个很直观的想法就是,第一次调用的时候就把答案记下来,之后调用不重新算,直接返回之前已经计算出的答案即可。——这就是记忆化搜索。

这是有障碍的情况,
mp[x][y]==-1表示有障碍
在有一些dp问题中,状态之间的转移顺序不是那么确定,并不能像一些简单问题一样写几个for循环就解决了。
我们可以直接计算最终要求的状态,然后在求这个状态的过程中,要调用哪个子状态就直接调用即可,但是每一个状态调用一遍之后就存下来答案,下次计算的时候就直接取答案即可,就不需要从新再计算一遍。
虽然看上去每一次都计算不少,但是因为每一个状态都计算一次,所以均摊下来,复杂度还是状态数*状态转移。
拓扑图 DP
拓扑图dp通常是在拓扑图上求关于所有路径的某种信息之和。当然这里的“和”的运算法则可以是加法或是取max和min。或者其他定义的运算。
按拓扑序沿着有向边转移就可以了。
BZOJ 4562 食物链
给定n个点m条边的有向无环食物网,求其中有多少条极长食物链。
n<=105,m<=2*105
题解
拓扑图dp经典题
设f[u]为以节点u为终点的食物链数量。
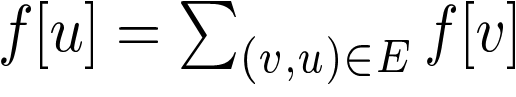
按照拓扑序的顺序转移即可。
基础DP练习题
最大子矩阵
在n*n的整数矩阵中找一个最大的子矩阵,最大化元素和。
N<=100
题解
枚举上下边界,然后只需要确定左右边界,就是个一维的问题,实际上就是求最大连续子段和。
F[i]=max(0, f[i-1])+val[i];
val[i]表示枚举的上下界范围内第i列的和。
下午
序列上的 DP
区间上的 dp 状态设计最基本的形式◦
F[i] 表示以 i 结尾的最优值或方案数。
F[i][k]表示以i结尾附加信息为k的最优值或方案数。
当然可以有多维附加信息。◦转移的话往往是枚举上一个断点。
F[i]=max { F[j]+ w(j+1, i) | j 是一个满足转移条件的断点}。
另一个很常见的是:fi前i个位置分成j段/选出j个的最优值。
这是最简单的一类序列上的 dp。
bzoj1003
有 m 个码头和 e 条航线,每天航线有成本。有连续 n 天需要从 1 号码头到 m 号码头运输货物。每个码头会在某些天数区间内不许经过。每更换一次运输路线,要付出 k 的成本。
求这 n 天的最小总成本。
m<=20,n<=100
不需要多维的来表示,只需要设 f[i] 表示前 i 天的最小花费
其实就是分成很多段,每一段选同一个运输路线,然后得到一个最优的划分方案,使得成本最小。
f[i] 表示前 i 天的运输最小成本。
f[i]=min{ f[j]+k+w(j+1, i)*(i-j) | j<i}
其中 w(x, y) 表示最短的在第 x 天到第 y 天都能用的路线长度,把能在则几天一直走的点加进图中,跑最短路径即可。◦复杂度 O(N^2 * m * log(m))
括号序列模型及解法
Codeforces314E
给定一个长度为n的仅包含左右括号和问号的字符串,将问号变成左括号或右括号使得该括号序列合法,求方案总数。
例如(())与()()都是合法的括号序列。
◦令dp[i][j]表示当前到第i个字符,现在还有j个左括号。(也就是前缀和为0),因为强制j大于0,所以不会出现问题
那么分三种情况考虑。
若第i+1个字符是左括号,则能转移到dp[i+1][j+1]。
若第i+1个字符是右括号,则能转移到dp[i+1][j-1]。
若第i+1个字符是问号,则能转移到dp[i+1][j-1]与dp[i+1][j+1]。
最终dp[n][0]就是方案总数啦。
时间复杂度为O(n^2)。
bzoj4922
给出一些括号序列,要求选择一些括号序列拼接成一个合法的括号序列,使得总长最大。
1<=n<=300,表示括号序列的个数
括号序列的长度len不超过300.
首先对于每个括号序列,把左边的左括号和右边的右括号对消,最后能得到一坨这样的东西:
))…))((…((
就是x个右括号然后y个左括号,记作(x, y)
然后考虑假如我们的子集选好了,我们要按照什么顺序拼接才能拼成一个合法的括号序列呢?
BZOJ3709
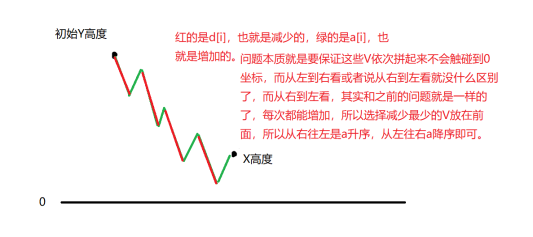
在一款电脑游戏中,你需要打败n只怪物(从1到n编号)。为了打败第i只怪物,你需要消耗d[i]点生命值,但怪物死后会掉落血药,使你恢复a[i]点生命值。任何时候你的生命值都不能降到0(或0以下)。
请问是否存在一种打怪顺序,使得你可以打完这n只怪物而不死掉。
N<=10^5
我们按照减血可以从后往前推
1:如果a[i]-d[i]>0,说明打掉这个怪兽有血可恢复,那么血量会变多,明显我们按照伤害d[i]从小到大排序即可,然后一个个杀下来。
2:如果a[i]-d[i]<0,说明会亏血。一个精妙的想法就是,最后剩余的血量值,假设是x,那么x是固定的。然后可以看作初始血量为x,怪兽的属性a, d交换,这样就和上一种情况一样了。 (如图)
再回到4922
我们还是
把左括号看成+1,右括号看成-1,同样是保证任意一个前缀大于等于0,且总和为0。
设f[i][j]为前i个括号序列-1与+1的和j个时选出括号序列最长的长度和。
也就是前i个括号序列左括号比右括号多j个时的最长的长度和。
转移时考虑下一个括号序列选不选即可。
Len[i] 为排完序后第i个括号序列的长度。
f[i + 1][j - L[i + 1] + R[i + 1]] < -f[i][j] + len[i + 1](j >= L[+1])
f[i + 1][j] < -f[i][j]◦ 最后答案就是f[n][0].
复杂度O(nlenlen);
Len[i]为排完序后第i个括号序列的长度。
f[i+1][j-L[i+1]+R[i+1]]f[i][j] + len[i+1] (j>=L[i+1])◦f[i+1][j]f[i][j]◦最后答案就是f[n][0]
复杂度O(nlenlen)
一套有趣的题目
1:1, 2, 3...n 以此进栈,求有多少种可能的出栈序列。
2:由n对括号形成的合法的括号序列由多少个。
N<=10^5
设fn表示n对括号的序列数,那么对于一对括号和其他的括号
()()
我们可以说
3:n个节点共能构成多少种二叉树, 左右子树是认为不同。
4: 凸多边形的三角划分的方案数:把一个凸多边形用n-3条直线连接n-3对顶点,共形成n-2个三角形,求方案数。
5:一个n*n的格子,从(0, 0)走到(n, n),求不跨过(0, 0)->(n, n)这条直线的路径方案数。向右看作+1,向上看作-1
其实是卡特兰数啦
只想背过这个

后面的咕了,md一万多字真的不想写了 over


 浙公网安备 33010602011771号
浙公网安备 33010602011771号