KMP

烤馍片是一种算法，这种算法我忘了就学，学了就忘，所以这里再写一遍加深印象（

KMP 这个东西呢它可以在 \(O(n+m)\) 的时间复杂度内完成字符串的匹配，虽然但是我用字符串哈希我做匹配不也一个道理吗？KMP 可以与处理出来一个叫 \(fail\) 的数组（也可以叫 \(next\)），可以完成很多很厉害的东西。

下面我们先来了解一下 \(fail\) 是干嘛的：定义函数 \(\operatorname{fail}(i)\) 为字符串长度为 \(i\) 的前缀 的 最长的与字符串本身不同的 后缀 与 前缀 相同的长度。这样说好像不太容易理解也不太严谨，我们炒个例子罢，比如字符串
s: a b a b a b c
\(\operatorname{fail}(5) = 3\)，什么意思嘞，就是说 a b a b a 中，前三个 a b a 和后三个 a b a 是一样的。那么对于 \(\operatorname{fail}(2)\) 呢？是 \(0\)。

\(\operatorname{fail}\) 可以这样求：首先 \(\operatorname{fail}(1) = 0\)，显然易见，下面我们假设已经求出来了 \(\operatorname{fail}(1\sim i - 1)\)，考虑到了 \(s_i\)，我们充分利用一下之前得到的信息：

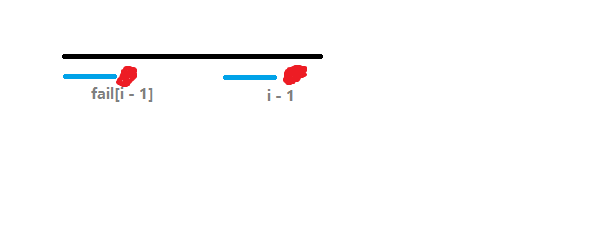
蓝色部分代表相同的，根据定义，左边的红色部分代表 \(str_{\operatorname{fail}(i - 1) + 1}\) 右边的红的代表 \(str_i\)，如果 \(str_i = str_{\operatorname{fail}(i - 1) + 1}\)（两个红的相等），是不是就说明一点：\(fail_i = fail_{i - 1} + 1\)？

那万一它们不相同呢？那我们退而求其次，像这样

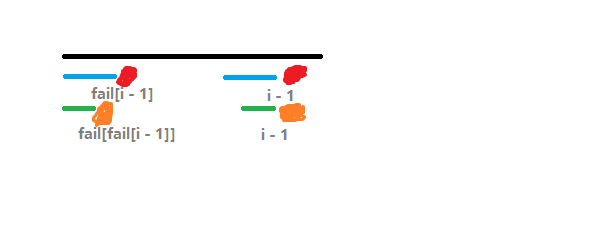
如果两个橙色的相等（\(str_{\operatorname{fail}(\operatorname{fail}(i - 1)) + 1} = str_{i + 1}\)），那么 \(fail_i = \operatorname{fail}(\operatorname{fail}(i - 1)) + 1\)。推广开来我们可以这样搞：对于求 \(fail_i\)，定义一个指针 \(j\)，\(j\) 一开始等于 \(j - 1\)。如果 \(str_{\operatorname{j} + 1} = str_i\)，说明这个行，\(\operatorname{fail}(i) = \operatorname{fail}(j)+1\)。否则 \(j = \operatorname{fail}(j)\)。原因的话相信看看图就不难理解了 qwq

---

求出来了 \(\operatorname{fail}\)，它有什么用呢？它可以搞字符串匹配。以这道题模板题 link 为例。我们先求出来了 \(s2\) 的 \(\operatorname{fail}\)。我们来手玩一个小样例

ABADBC
ABAC

首先它们登登登匹配到第三位，到了第四位发现 D 和 C 不一样，那么怎么办，从头再来？我们发现我们知道了 \(s1\) 前三位是 ABA，\(s2\) 的前三位也是 ABA，我们肯定不会这样匹配

ABA
 ABA

因为这肯定不行，聪明的我们会想到这样匹配

ABA
  ABA

深究一下其中的原因，因为这个 A 既是 ABA 的后缀，也是 ABA 的前缀……等等，\(\operatorname{fail}\)？这个相信是不难领会的，还可以举个例子

ABABAD
ABABAB

匹配到第五位失配了，但是 \(s1\) 前五位和 \(s2\) 前五位都是 ABABA，我们光来匹配这几个已知的，我们当然不会这样匹配

ABABA
 ABABA

而是

ABABA
  ABABA

因为这样肯定能匹配上一点。我们一定会从 \(\operatorname{fail}\) 开始，这相当于 \(\operatorname{fail}\) 前面都匹配过了。我们也容易理解为啥 \(\operatorname{fail}\) 要取最大——不取最大的话可能会漏。

这个算法就出来了：如果 \(i\) 是指向 \(s1\) 的，\(j\) 是指向 \(s2\) 的，前 \(i - 1\) 位与第 \(j\) 位匹配，现在我们考虑第 \(i\) 位与第 \(j + 1\) 位。如果能匹配就匹配，不能匹配那么让 \(j = \operatorname{fail}(j)\)，如果 \(str_{i} = str_{j + 1}\)，那么就匹配成功，否则就再让 \(j = \operatorname{fail}(j)\) 以此类推。

代码

//SIXIANG
#include <iostream> 
#include <string>
#define MAXN 1000000
#define QWQ cout << "QWQ" << endl;
using namespace std;
int fail[MAXN + 10];
void init() {
	string s1, s2;
	cin >> s1 >> s2;
	s1 = " " + s1, s2 = " " + s2;
	
	fail[1] = 0;
	for(int p = 2; p < s2.size(); p++) {
		int i = fail[p - 1];
		while(s2[i + 1] != s2[p] && i) i = fail[i];
		if(s2[i + 1] == s2[p]) fail[p] = i + 1;
		else fail[p] = i;
	}
	
	int i = 0, end = s2.size() - 1;
	for(int p = 1; p < s1.size(); p++) {
		while(s2[i + 1] != s1[p] && i) i = fail[i];
		if(s2[i + 1] == s1[p])
			i++;
		if(i == end) cout << p - end + 1 << endl;
	}
	for(int p = 1; p < s2.size(); p++)
		cout << fail[p] << ' ';
} 
int main() {
	init();
} 

---

可是很显然我随手搓一个字符串哈希，比这个起码要好理解很多，效率也是 \(O(n+m)\) 的呀。这里面的 \(\operatorname{fail}\) 有一个很厉害的作用。比如说有一道题根字符串的循环节有关系，我们就可以用 \(\operatorname{fail}\)。比如说这道题 link。

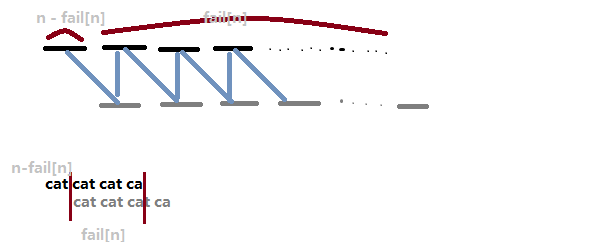
先给出结论，答案是 \(n - \operatorname{fail}(n)\)。为啥捏？

相信这张图相当明白了（）

那么别的拓展也能轻而易举的得到，如果 \((n-\operatorname{fail}(n))|n\)，那么这个字符串一定能由前 \(len = n - \operatorname{fail}(n)\) 个字符重复 \(n/len\) 次形成。