FFT 学习笔记
首先就是中考这几天我们学校做考场,然后初二放假在家写作业。
然后我就摸鱼来推之前不会的 FFT 的式子,推一推发现诶麻麻我懂了!麻麻我悟了麻麻!
于是在放假第二天我写下了这样一篇学习笔记 qwq
多项式的系数表示和点值表示
我们都知道,一个 \(n\) 项多项式,如果我们写成一个函数,就可以写成这样:
\(f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \dots + a_{n - 1}x^{n - 1}\)
如果我们有两个 \(n\) 项的多项式 \(f\) 与 \(g\),然后我们想要算它们俩的乘积应该怎么办呢?似乎我们只能 \(O(n^2)\)。
我们都知道,两点确定一个一次函数,三点确定一个二次函数,推广开来,\(n\) 个点可以确定一个 \(n\) 项的多项式。如果我们取出了 \(n\) 个横坐标 \(\{x_1, x_2, \dots, x_n\}\),然后我们算出来了 \(f\) 与 \(g\) 它们对应的横坐标的点集,\(\{(x_1, f(x_1)), (x_2, f(x_2)), \dots, (x_n, f(x_n))\}\) 和 \(\{(x_1, g(x_1)), (x_2, g(x_2)), \dots, (x_n, g(x_n))\}\)
横坐标不变,纵坐标相乘,得到新的 \(n\) 个点 \(\{(x_1, f(x_1)g(x_1)), (x_2, f(x_2)g(x_2)), \dots, (x_n, f(x_n)g(x_n))\}\) 这 \(n\) 个点一定在 \(f\) 与 \(g\) 的乘积的函数上。
这是相当好理解的。由于 \(n\) 点确定一个 \(n\) 项式,事实上我们已经知道了 \(f\) 乘 \(g\) 对不对?时间复杂度就是刚刚的相乘,也就是 \(O(n)\)。
快去开香槟!但事实上我们求点的复杂度为 \(O(n^2)\)。由于正常人都不会用 \(n\) 个点表示一个 \(n\) 项式,所以我们还要把这 \(n\) 个点转化成系数表达法才行,然后就要用高斯消元,时间复杂度 \(O(n^3)\)。
那我还不如暴力对吧,但是,事实上这给了我们启发,有没有一种方法能够取一些非常厉害的 \(x\),能让我们加速求出 \(n\) 个对应点的纵坐标(这叫插值)和加速求出系数(这叫还原) 呢?
这就有了傅里叶变换了~
一些前置知识
虚数和复数
1 虚数
我们定义 \(i = \sqrt{-1}\),\(i\) 就是虚数单位。你可能会像曾经的我一样纠结于 \(i\) 是啥啊它是啥数啊它究竟是什么啊 QAQ 之类的问题。但是事实上 \(i\) 啥都不是,反正就是个符号(
2 复数
这可不是我们说的负数,而是复数,就是一个实数和一个虚数构成,一般用 \(z\) 表示,记为 \(z = a + bi\),其中 \(a\) 为实数,叫 \(z\) 的实部,\(bi\) 为虚数,叫 \(z\) 的虚部。
值得一提的是,\(z\) 可以在平面直角坐标系上用向量清晰地刻画出来。如图,从源点到点 \((2, 3)\) 构成一个向量,这条向量就代表复数 \(z = 2+3i\)。这里的纵轴叫虚轴(纵坐标代表虚部的 \(b\)),横轴叫实轴(横坐标代表实部的 \(a\))
3 单位圆和单位根
在上图突兀的闯入了一个以原点为圆心,\(1\) 为半径的圆,这个圆很厉害,它的名字叫单位圆。单位圆有什么用呢?如果我们将单位圆 \(n\) 等分,画出 \(n\) 条半径,它们所对应的复数是 \(x^n = 1\) 的一个复数根。
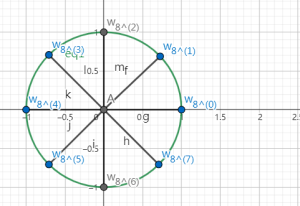
比如这张图 \(n = 8\)(其实我标点的时候想标成 \(w_n^k\) 但是这个只能给我标成这个样子,大家凑合看吧 qwq)
从 \((1, 0)\) 开始将单位圆平分成 \(8\) 等分,有 \(8\) 条半径,从 \(0\) 开始逆时针编号,一直到 \(n - 1\)。每一个半径都对应着一个复数,我们记第 \(k\) 条半径的这个复数为 \(w_n^k\),很显然,\(w_n^0 = 1\)。其中 \((w_n^k)^n = 1\),具体而言我不会证(
然后呢?由于我们学过三角函数,我们容易得到 \(w_n^k = \cos(2\pi k/n) + i \sin(2\pi k / n)\)。同时还有 \(w_n^k = (w_n^1) ^k\),也就是说这个 \(k\) 可以看成 \(w_n^1\) 的指数,而不仅仅是一个上标(这条我也不会证,我太菜了 QAQ)
4 单位根的性质
-
折半定理
\(w_n^k = w_{2n}^{2k}\)。
相信大家看看上面的图就懂了。如果喜欢理性荔枝地证明的话——
\(w_n^k = \cos(2\pi k / n) + i \sin(2\pi k / n)\\ = \cos(2\pi (2k / 2n)) + i \sin(2\pi(2k / 2n)) \\ = w_{2n}^{2k}\) -
消去定理
\(w_n ^k = -w_n ^{k - n / 2}\)(\(n\) 是偶数,\(k \le n / 2\))。
一看图相信大家都明白啦,因为它俩关于原点对称,等大反向。
相信这些对大家都不难!了解了这些,FFT 就很容易啦~
FFT
插值
FFT 是用分治做的,所以下面我们默认 \(n\) 为 \(2\) 的整数次幂。
FFT 的精华在于倒式子,这个式子虽然很长,但是很好理解,相信大家都能看懂!ヾ(◍°∇°◍)ノ゙
\(f(x) = a_0 + a_1x + a_2x^2 + \dots a_{n - 1}x^{n - 1} \\ = (a_0 + a_2x_2 + a_4x_4 + \dots a_{n - 1}x^{n - 1}) + \\ (a_1x+ a_3x^3 + a_5x^5 + \dots a_{n - 2}x^{n - 2})\)
这一步是将下标按照奇偶性分类。我们定睛一看,发现这两边很相似,很漂亮,为了化简我们新定义两个函数
\(A_1(x) = a_0 + a_2x + a_4x^2 + \dots + a_{n - 1}x^{(n - 1) / 2}\)
\(A_2(x) = a_1 + a_3x + a_5x^2 + \dots + a_{n - 1}x^{(n - 1) / 2 - 1}\)
然后 \(f(x) = A_1(x^2) + xA_2(x^2)\)
FFT 最巧妙的一步在于,它代入的是 \(n\) 的单位根们,\(w_n^1, w_n^2, \dots w_n^{n - 1}\)。
所以就有 \(f(w_n^k) = A_1((w_n ^ k) ^ 2) + w_n ^ k A_2((w_n ^ k) ^ 2) \\ = A_1(w_n^{2k}) + w_{n}^k A_2(w_n^{2k})\)
第三步是因为 \(w_n ^k\) 的上标可以看成 \(w_n ^1\) 的指数
下面简单的分讨一下。
对于 \(k \le n / 2\),\(f(w_n^k) = A_1(w_n^{2k}) + w_{n}^k A_2(w_n^{2k}) \\ = A_1(w_{n / 2}^k) + w_n^kA_2(w_{n / 2}^k)\)。这是因为折半定理
对于 \(k > n / 2\),\(w_n^k = -w_{n} ^{k - n / 2}\),两边同时平方一下就有了 \(w_n^{2k} = w_n^{2k-n}\),再用折半定理,就能得到 \(w_{n / 2} ^k = w_{n / 2} ^{k - n / 2}\)。
所以呢 \(f(w_n^k) = A_1(w_n^{2k}) + w_{n}^k A_2(w_n^{2k}) \\ = A_1(w_{n / 2}^k) + w_n^kA_2(w_{n / 2}^k) \\ = A_1(w_{n / 2}^{k - n / 2}) - w_n^{k - n /2 }A_2(w_{n / 2}^{k - n / 2})\)。
\(k - n / 2 < n / 2\),诶这个问题我刚刚不解决过了嘛!
所以我们就可以分治,先分治处理 \(A_1\),再分治处理 \(A_2\),然后就是按照上面的式子合并 \(A_1, A_2\),最后我们就可以得到啦~
时间复杂度是经典的 \(T(n) = 2T(n / 2) + n\),也就是 \(O(n\log_2 n)\)
还原
那么怎么点值转系数呢?
下面要简单的做一个小推导 qwq
比如多项式 \(f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \dots + a_{n - 1}x^{n - 1}\),我们刚刚傅里叶变换出来了 \(\{f(w_n^0), f(w_n ^ 1), \dots, f(w_n ^ {n - 1})\}\),我们记它们为 \(\{b_0, b_1, b_2, \dots, b_{n - 1}\}\)。
然后我们新构造一个多项式 \(g(x) = b_0 + b_1x + b_2x^2 + b_3x^3 + \dots + b_{n - 1}x^{n - 1}\),然后我们将 \(w_n^k\) 的倒数 \(w_n^{-k}\) 弄出来代入得到 \(\{g(w_n^0), g(w_n ^ {-1}), \dots, g(w_n ^ {1-n})\}\)(这些倒数很显然满足折半和消去定理),我们记它为 \(\{c_0, c_1, c_2, \dots, c_{n - 1}\}\)。傅里叶:有完没完啊啊啊啊啊
然后我们开始推导 $c_k = g(w_{n}^{-k}) = \sum\limits_{i = 0}^{n - 1}b_i w_{n}^{-ik} \ = \sum\limits_{i = 0}^{n - 1}((\sum\limits_{j= 0}^{n - 1}a_j w_n ^ {ij})w_{n}^{-ik}) \ = \sum\limits_{i = 0}^{n - 1}(\sum\limits_{j= 0}^{n - 1}a_j w_n ^ {(j - k)i}) \ = \sum\limits_{j = 0}^{n - 1} a_j(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i}) $
当 \(j = k\) 时,\(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i} = \sum\limits_{i= 0}^{n - 1}w_n ^ 0 = n\)
当 \(j \not = k\) 时,\(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i}\) 这一坨实际上是一个首项为 \(1\),公比为 \(w_{n}^{j - k}\) 的等比数列!
所以 \(\sum\limits_{i= 0}^{n - 1}w_n ^ {(j - k)i}) = \dfrac{w_n^{n(j - k)} - 1}{w_n^{j - k} - 1} = \dfrac{1^{(j - k)} - 1}{w_n^{j - k} - 1} = 0\)
所以 \(c_k = na_k\),即 \(a_k = \dfrac{c_k}{n}\)。
等等!我们似乎找到了系数和点值的关系!
这就是 FFT 还原的方法
先对 \(f\) 做一遍插值,再用插值得到的点值为系数,构造一个新的多项式 \(g\),代入单位根的倒数 \(w_n^0, w_n^{-1}, \dots, w_n^{1 - n}\) 到 \(g\) 里面去,再做一遍插值。所得的点值除以 \(n\) 就是 \(f\) 的各项系数。
代码(递归):
//SIXIANG
#include <iostream>
#include <cmath>
#define MAXN 3000000
#define QWQ cout << "QWQ" << endl;
using namespace std;
int n, m;
double A[MAXN + 10], B[MAXN + 10];
const double pi = acos(-1);
struct complex {
double a, b;
};
complex rt1[MAXN + 10], rt2[MAXN + 10], rt3[MAXN + 10], g[MAXN + 10];
complex operator + (const complex x, complex y) {return (complex){x.a + y.a, x.b + y.b};}
complex operator - (const complex x, complex y) {return (complex){x.a - y.a, x.b - y.b};}
complex operator * (const complex x, complex y) {return (complex){x.a * y.a - x.b * y.b, x.a * y.b + x.b * y.a};}
//f**k f**k t*d
void fft(int len, complex *arr, int type) {
if(len <= 1) return ;
for(int p = 0; p < len; p += 2) {
g[p / 2] = arr[p];
g[p / 2 + len / 2] = arr[p + 1];
}
for(int p = 0; p < len; p++) arr[p] = g[p];
fft(len / 2, arr, type);
fft(len / 2, arr + len / 2, type);
complex dwg = (complex){cos(2.0 * pi / len), type * sin(2.0 * pi / len)};
complex w = (complex){1, 0};
for(int p = 0; p < len / 2; p++, w = w * dwg) {
g[p] = arr[p] + w * arr[p + len / 2];
g[p + len / 2] = arr[p] - w * arr[p + len / 2];
}
for(int p = 0; p < len; p++)
arr[p] = g[p];
}
void init() {
int bas = 1;
while(bas <= n + m)
bas *= 2;
fft(bas, rt1, 1);
fft(bas, rt2, 1);
for(int p = 0; p < bas; p++)
rt3[p] = rt1[p] * rt2[p];
fft(bas, rt3, -1);
for(int p = 0; p <= n + m; p++)
cout << int(rt3[p].a / bas + 0.5) << ' ';
}
int main() {
cin >> n >> m;
for(int p = 0; p <= n; p++) cin >> rt1[p].a;
for(int p = 0; p <= m; p++) cin >> rt2[p].a;
init();
}
优化
我们知道递归它很慢,然后 FFT 又涉及到复数,所以就更慢了,所以 1e6 的话递归可能跑不过去,我们要把它改成迭代的。
咋迭代呢?我们以 \(n = 8\) 为例。
0 1 2 3 4 5 6 7
0 2 4 6|1 3 5 7
0 4|2 6|1 5|3 7
0|4|2|6|1|5|3|7
(这个图你都要偷懒???)
这就是 FFT 递归中的奇偶划分,最后得到这一串数
0 4 2 6 1 5 3 7,看上去没什么规律的样子,我们充分发扬人类智慧写出它们的二进制,就有 000 100 010 110 001 101 011 111。看上去还是没有任何规律的样子,所以我们把它的二进制反转一下,就有了 000 001 010 011 100 101 110 111。
发现什么了没有?反转二进制后就是 0 1 2 3 4 5 6 7!
一个结论:对于 \(0\sim (n - 1)\),FFT 奇偶划分后最后顺序,为写成 \(\log_2 n\) 位二进制后反转后得到的
我不会证明,但我会瞪眼观察(doge)
也就是说我们只要按照这个顺序就可以迭代了!
为了方便理解我先把代码贴上来 qwq
void fft(int len, complex *arr, int type) {
for(int p = 0; p < len; p++)
if(p < ord[p]) swap(arr[p], arr[ord[p]]);
for(int p = 1; p < len; p <<= 1) {
complex dwg = (complex){cos(pi / p), type * sin(pi / p)};
for(int i = 0; i < len; i += (p << 1)) {
complex w = (complex){1, 0};
for(int j = 0; j < p; j++, w = w * dwg) {
complex x = arr[i + j], y = w * arr[i + j + p];
arr[i + j] = x + y, arr[i + j + p] = x - y;
}
}
}
}
这个代码还是很好理解的 qwq
\(ord_i\) 代表 \(i\) 应该在的地方,它可以这么求
for(int p = 0; p < bas; p++)
ord[p] = (ord[(p >> 1)] >> 1) | ((p & 1) << (qwq - 1));
其中 \(qwq = \log_2 n\),这个东西我不是很会证,没关系背下来就好了(雾)
FFT 的精华推导反正都推出来了嘛/kel(
//SIXIANG
#include <iostream>
#include <cmath>
#define MAXN 3000000
#define QWQ cout << "QWQ" << endl;
using namespace std;
int n, m;
double A[MAXN + 10], B[MAXN + 10];
const double pi = acos(-1);
struct complex {
double a, b;
};
complex rt1[MAXN + 10], rt2[MAXN + 10], rt3[MAXN + 10], g[MAXN + 10];
complex operator + (const complex x, complex y) {return (complex){x.a + y.a, x.b + y.b};}
complex operator - (const complex x, complex y) {return (complex){x.a - y.a, x.b - y.b};}
complex operator * (const complex x, complex y) {return (complex){x.a * y.a - x.b * y.b, x.a * y.b + x.b * y.a};}
int ord[MAXN + 10];
//f**k f**k t*d
void fft(int len, complex *arr, int type) {
for(int p = 0; p < len; p++)
if(p < ord[p]) swap(arr[p], arr[ord[p]]);
for(int p = 1; p < len; p <<= 1) {
complex dwg = (complex){cos(pi / p), type * sin(pi / p)};
for(int i = 0; i < len; i += (p << 1)) {
complex w = (complex){1, 0};
for(int j = 0; j < p; j++, w = w * dwg) {
complex x = arr[i + j], y = w * arr[i + j + p];
arr[i + j] = x + y, arr[i + j + p] = x - y;
}
}
}
}
void init() {
int bas = 1, qwq = 0;
while(bas <= n + m)
bas *= 2, qwq++;
for(int p = 0; p < bas; p++)
ord[p] = (ord[(p >> 1)] >> 1) | ((p & 1) << (qwq - 1));
fft(bas, rt1, 1);
fft(bas, rt2, 1);
for(int p = 0; p < bas; p++)
rt3[p] = rt1[p] * rt2[p];
fft(bas, rt3, -1);
for(int p = 0; p <= n + m; p++)
cout << int(rt3[p].a / bas + 0.5) << ' ';
}
int main() {
cin >> n >> m;
for(int p = 0; p <= n; p++) cin >> rt1[p].a;
for(int p = 0; p <= m; p++) cin >> rt2[p].a;
init();
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号