05_Java数组
1、数组概述
-
数组的定义
- 数组是相同类型数据的有序集合
- 数组描述的是相同类型的若干个数据,按照一定的先后次序排列组合而成
- 其中,每个数据称作一个数组元素,每个数组元素可以通过一个下标来访问他们
2、数组声明创建
-
首先必须声明数组变量,才能在程序中使用数组。语法如下:
dataType[] arrayRefVar; //首选的方法 //或 dataType arrayRefVar[]; //效果相同,但不是首选方法 -
Java语言使用new操作符来创建数组,语法如下:
dataType[] arrayRefVar = new dataType[arraySize]; -
数组的元素是通过索引访问的,数组索引从0开始。
-
获取数组的长度:arrays.length
-
示例代码:
public static void main(String[] args) { //1、声明一个数组 int[] numbers; //2、创建一个数组 numbers = new int[10]; //3、给数组元素中赋值 numbers[0] = 1; numbers[1] = 2; numbers[2] = 3; numbers[3] = 4; numbers[4] = 5; numbers[5] = 6; numbers[6] = 7; numbers[7] = 8; numbers[8] = 9; numbers[9] = 10; //遍历数组计算数组中元素的和 int sum = 0; for (int number : numbers) { sum += number; } System.out.println(sum); } -
内存分析
-
Java内存分析:
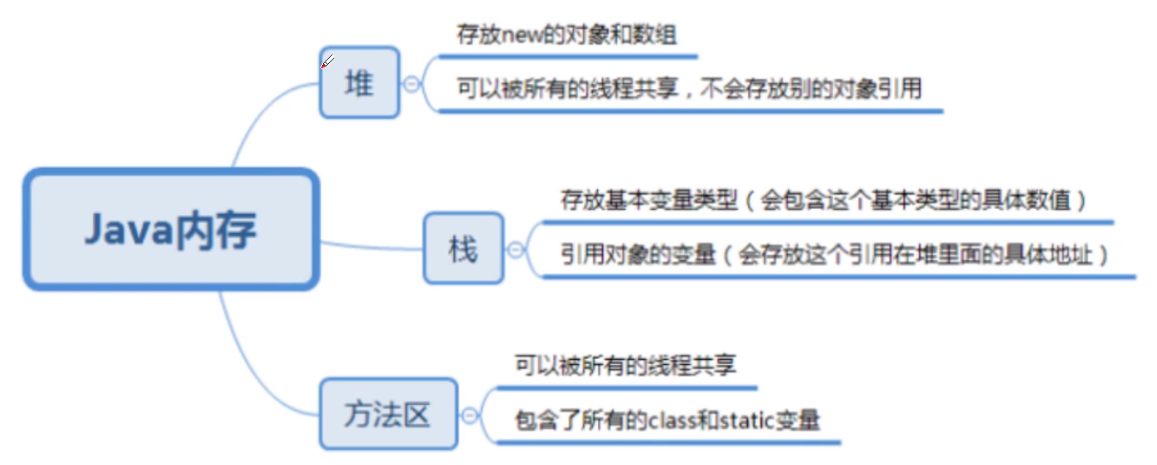
-
写代码画图分析内存!
-
上面示例代码在内存中的解析如下图:
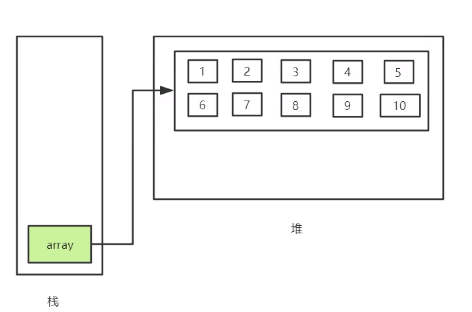
-
-
三种初始化
-
静态初始化
int[] a = {1, 2, 3}; -
动态初始化
int[] a = new int[2]; a[0] = 1; a[1] = 2; -
数组的默认初始化
- 数组是引用类型,它的元素相当于类的实例变量,因此数组一经分配空间,其中的每个元素也被按照实例变量同样的方式被隐式初始化。
-
-
数组的四个基本特点
- 其长度是确定的。数组一旦被创建,它的大小就是不可以改变的。
- 其元素必须是相同类型,不允许出现混合类型。
- 数组中的元素可以是任何数据类型,包括基本类型和引用类型。
- 数组变量属引用类型,数组也可以看成是对象,数组中的每个元素相当于该对象的成员变量。数组本身就是对象,Java中对象是在堆中的,因此数组无论保存原始类型还是其他对象类型,数组对象本身是在堆中的。
-
数组边界
-
下标的合法区间:[0, length - 1],如果越界就会报错
public static void main(String[] args) { int[] a = new int[2]; System.out.println(a[2]); } -
ArrayIndexOutOfBoundsException:数组下标越界异常!
-
-
小结:
- 数组是相同数据类型(数据类型可以为任意类型)的有序集合
- 数组也是对象。数组元素相当于对象的成员变量
- 数组长度是确定,不可变的。如果越界,则报ArrayIndexOutOfBoundsException
3、数组的使用
-
普通for循环
public static void main(String[] args) { int[] arrays = {1, 2, 3, 4, 5}; int sum = 0; for (int i = 0; i < arrays.length; i++) { sum += arrays[i]; } System.out.println(sum); } -
for-each循环
public static void main(String[] args) { int[] arrays = {1, 2, 3, 4, 5}; int sum = 0; for (int i : arrays) { sum += arrays[i]; } System.out.println(sum); } -
数组作为方法入参
public static void main(String[] args) { int[] arrays = {1, 2, 3, 4, 5}; printArray(arrays); } //打印数组 public static void printArray(int[] arrays) { for (int i : arrays) { System.out.println(i); } } -
数组作为返回值
public static void main(String[] args) { int[] arrays = {1, 2, 3, 4, 5}; int[] results = reverse(arrays); for (int i : results) { System.out.println(i); } } //反转数组 public static int[] reverse(int[] arrays) { int[] results = new int[arrays.length]; for (int i = 0, j = arrays.length - 1; i < arrays.length; i++, j--) { results[i] = arrays[j]; } return results; }
4、多维数组
-
多维数组可以看成是数组的数组,比如二维数组就是一个特殊的一维数组,其每一个元素都是一个一维数组。
-
二维数组
int a[][] = new int[2][5];以上二维数组a可以看成一个两行五列的数组
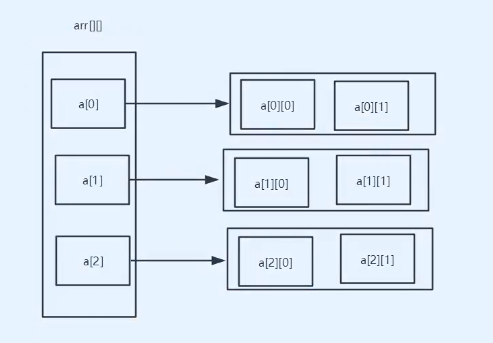
-
示例代码:
public static void main(String[] args) { int[][] array = {{1, 2}, {3, 4}, {5, 6, 7}}; for (int i = 0; i < array.length; i++) { for (int j = 0; j < array[i].length; j++) { System.out.print(array[i][j] + "\t"); } } }输出结果:1 2 3 4 5 6 7
5、Arrays类
-
数组的工具类java.util.Arrays
-
由于数组对象本身并没有什么方法可以供我们调用,但API中提供了一个工具类Arrays供我们使用,从而可以对数据对象进行一些基本的操作。
-
看看JDK帮助文档
-
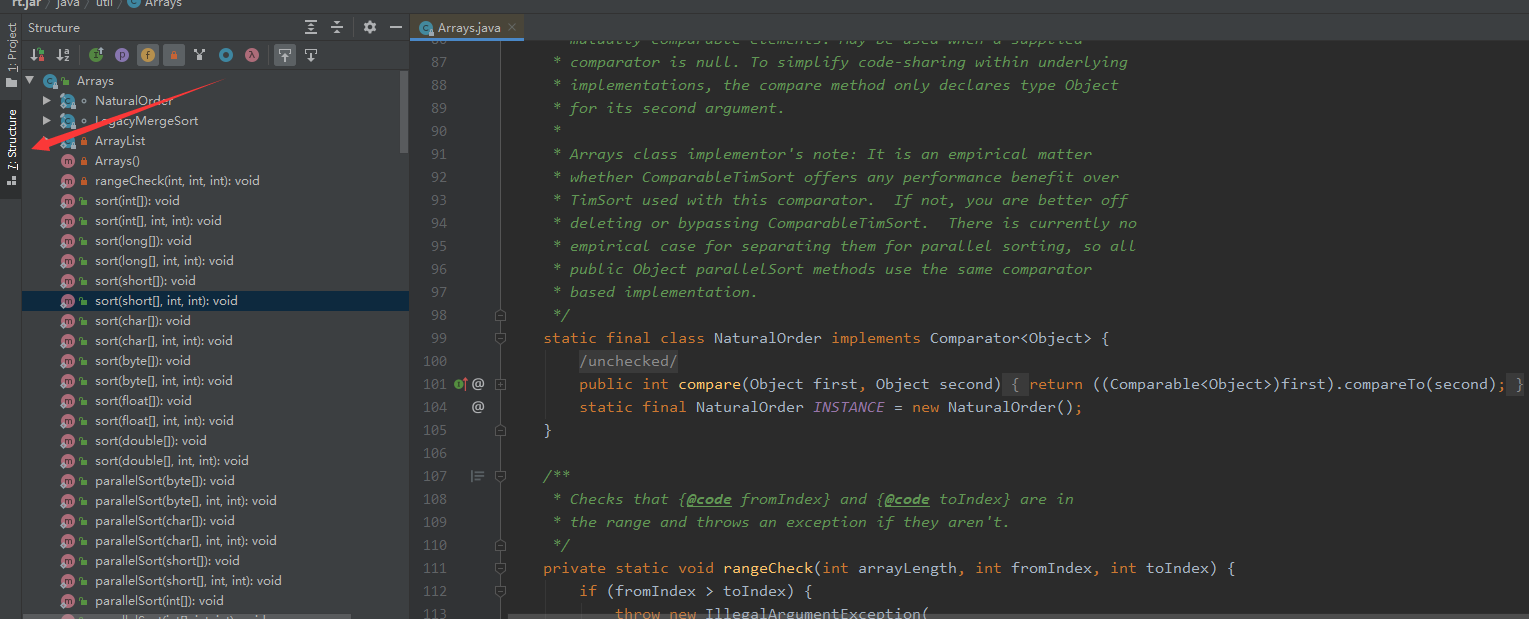
也可以通过IDEA来进行查看,ctrl + 点击Arrays类,然后通过Structure来查看整个类的结构。如下图:
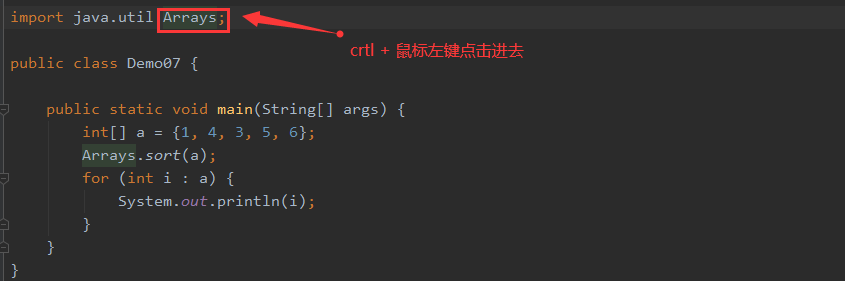
-
Arrays类中的方法都是static修饰的静态方法,在使用的时候可以直接使用类名进行调用,而"不用"使用对象来调用(注意:是"不用”而不是“不能")
-
具有以下常用功能:
-
打印数组元素:通过toString方法
public static void main(String[] args) { int[] a = {1, 4, 3, 5, 6}; System.out.println(Arrays.toString(a)); }输出结果:[1, 4, 3, 5, 6]
-
给数组赋值:通过fill方法
public static void main(String[] args) { int[] a = new int[8]; Arrays.fill(a, 2); System.out.println(Arrays.toString(a)); }输出结果:[2, 2, 2, 2, 2, 2, 2, 2]
-
对数组排序:通过sort方法,按升序
public static void main(String[] args) { int[] a = {5, 4, 3, 2, 1, 6}; Arrays.sort(a); for (int i : a) { System.out.print(i + "\t"); } }输出结果:1 2 3 4 5 6
-
比较数组:通过equals方法比较数组中元素值是否相等
public static void main(String[] args) { int[] a = {5, 4, 3, 2, 1, 6}; int[] b = {1, 2, 3, 5, 6}; int[] c = {1, 2, 3, 5, 6}; boolean b1 = Arrays.equals(a, b); boolean b2 = Arrays.equals(b, c); System.out.println(b1 + ", " + b2); }输出结果:false, true
-
查找数组元素:通过binarySearch方法能对排序好的数组进行二分查找法操作。
-
6、稀疏数组
-
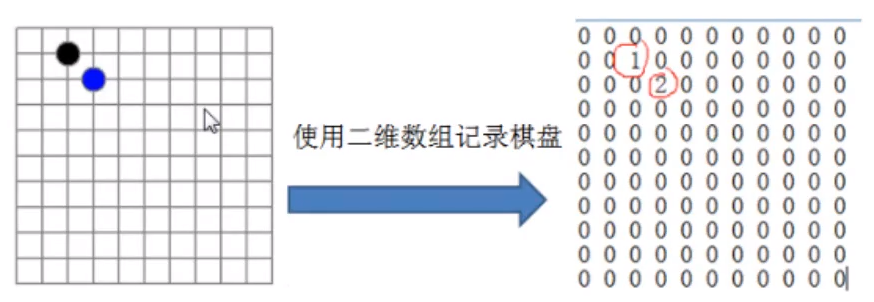
需求:编写五子棋游戏中,有存盘退出和续上盘的功能。
-
分析问题:因为该二维数组的很多值默认值都是0,因此记录了很多没有意义的数据
-
解决:稀疏数组
6.1、稀疏数组介绍
-
当一个数组中大部分元素为0,或者为同一值的数组时,可以使用稀疏数组来保存该数组。
-
稀疏数组的处理方式:
- 记录数组一共有几行几列,有多少个不同值
- 把具有不同值的元素和行列及值记录在一个小规模的数组中,从而缩小程序的规模
-
如下图:左边是原始数组,右边是稀疏数组
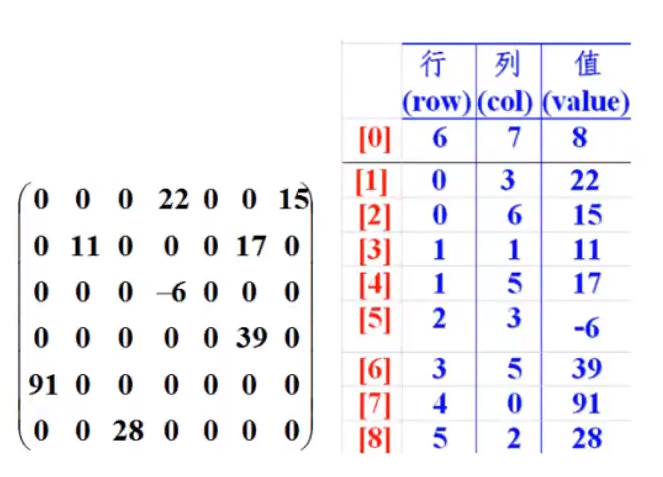
6.2、稀疏数组使用
-
示例代码,以存棋盘为例,把原始棋盘转存为稀疏数组,再还原为原始棋盘:
public static void main(String[] args) { //1、创建一个二维数组11*11 0:没有棋子 1:黑棋 2:白棋 int x = 11, y = 11; int[][] array1 = new int[x][y]; array1[1][2] = 1; array1[2][3] = 2; //输出原始数组 System.out.println("1、输出原始数组:"); for (int[] ints : array1) { for (int anInt : ints) { System.out.print(anInt + "\t"); } System.out.println(); } System.out.println("=========================================="); //2、获取原始数组的有效值个数 int sum = 0; for (int[] ints : array1) { for (int anInt : ints) { if (anInt != 0) { sum++; } } } System.out.println("2、有效值个数为:" + sum); System.out.println("=========================================="); //3、创建一个稀疏数组的数组 int[][] array2 = new int[sum + 1][3]; //给第一组数据赋值,存共几行几列几个有效数字 array2[0][0] = x; array2[0][1] = y; array2[0][2] = sum; //4、遍历二维数组,将非零的值,存放到稀疏数组中 int count = 1; for (int i = 0; i < array1.length; i++) { for (int j = 0; j < array1[i].length; j++) { if (array1[i][j] != 0) { array2[count][0] = i; array2[count][1] = j; array2[count][2] = array1[i][j]; count++; } } } System.out.println("3、输出稀疏数组:"); System.out.println("行\t列\t值"); //输出稀疏数组 for (int[] i : array2) { for (int j : i) { System.out.print(j + "\t"); } System.out.println(); } System.out.println("=========================================="); System.out.println("4、还原原始数组:"); //5、读取稀疏数组第一组数组重新构建一个原始数组 int[][] array3 = new int[array2[0][0]][array2[0][1]]; //6、给其中的元素还原它的值 for (int i = 1; i < array2.length; i++) { array3[array2[i][0]][array2[i][1]] = array2[i][2]; } //输出还原的数组 for (int[] i : array3) { for (int j : i) { System.out.print(j + "\t"); } System.out.println(); } }输出结果:
1、输出原始数组: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ========================================== 2、有效值个数为:2 ========================================== 3、输出稀疏数组: 行 列 值 11 11 2 1 2 1 2 3 2 ========================================== 4、还原原始数组: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
7、排序算法
- 把一个无序序列通过某种方式变成一个有序序列
7.1、冒泡排序
-
冒泡排序无疑是最为出名的八大排序算法之一!
-
冒泡的代码还是相当简单的,两层循环,外层冒泡轮数,里层依次比较,江湖中人人尽皆知。
-
我们看到嵌套循环,应该立马就可以得出这个算法的时间复杂度为O(n2)。
-
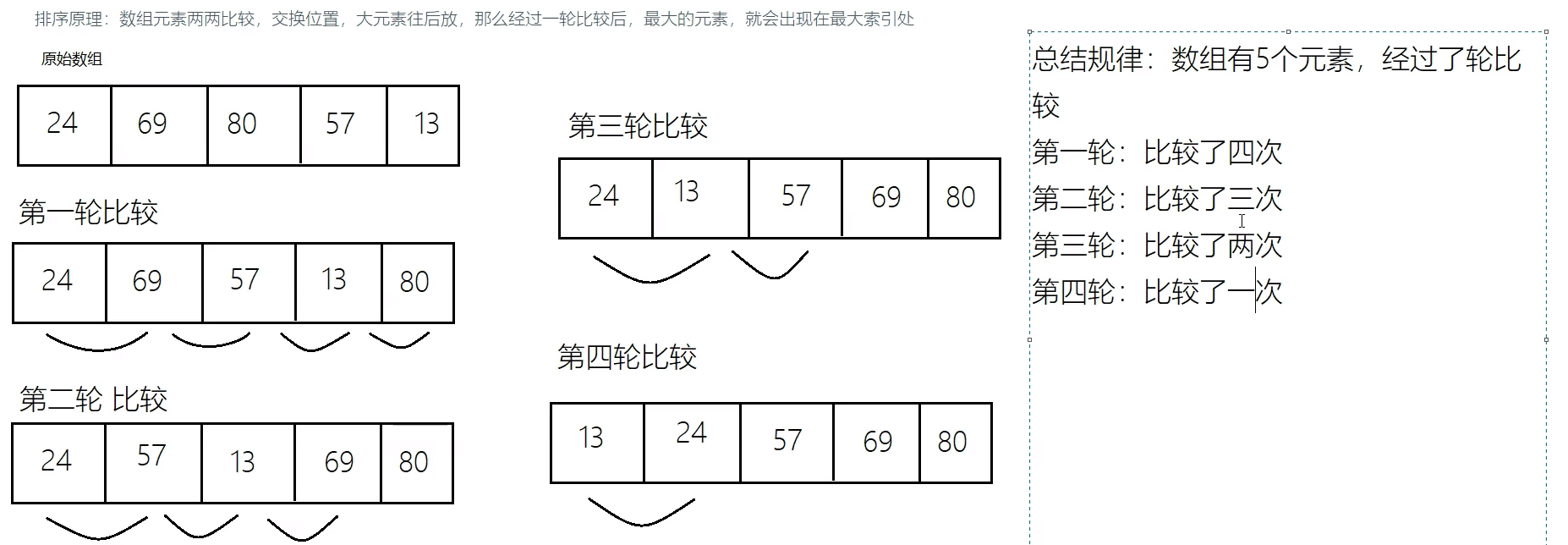
排序原理:数组元素两两比较,交换位置,大元素往后放,那么经过一轮比较后,最大的元素,就会出现在最大索引处。
-
代码实现:
public static void main(String[] args) { int[] a = {24, 69, 80, 57, 13}; sort(a); System.out.println(Arrays.toString(a)); } /** * 实现逻辑: * 1、比较数组中,两个相邻的元素,如果第一个数比第二个数大,则交换位置 * 2、每一次比较,都会产生一个最大的数,或最小的数 * 3、下一轮则可以减少一个排序! * 4、依次循环,直到结束 * @param array */ public static void sort(int[] array) { //临时变量 int temp; //外层循环,判断要走多少次,length-1是为了防止溢出(最后一个不用排序) for (int i = 0; i < array.length - 1; i++) { //通过flag标识位减少没有意义的比较 boolean flag = false; //内层循环,比较两个数,如果第一个数比第二个数大,则交换位置 for (int j = 0; j < array.length - 1 - i; j++) { //如果前一个数大于后一个数,则按正序排,反之,则按倒序排 if (array[j] > array[j + 1]) { temp = array[j]; array[j] = array[j + 1]; array[j + 1] = temp; flag = true; } } //如果是false,说明排序完成,则跳出循环,减少没有意义的比较 if (!flag) { break; } } }输出结果:[13, 24, 57, 69, 80]
7.2、选择排序
-
排序原理:从0索引处开始,依次和后面的元素进行比较,小的元素往前放,经过一轮比较后,最小的元素就出现在了最小所引处。

-
代码实现:
public static void main(String[] args) { int[] a = {24, 69, 80, 57, 13}; sort(a); System.out.println(Arrays.toString(a)); } public static void sort(int[] array) { int temp; for (int i = 0; i < array.length - 1; i++) { for (int j = i + 1; j < array.length; j++) { if (array[i] > array[j]) { temp = array[i]; array[i] = array[j]; array[j] = temp; } } } }输出结果:[13, 24, 57, 69, 80]
7.3、直接插入排序
-
排序原理:从1索引处开始,将后面的元素插入之前的有序列表中,使之保持有序。
-
代码实现:
public static void main(String[] args) { int[] a = {24, 69, 80, 57, 13}; sort(a); System.out.println(Arrays.toString(a)); } public static void sort(int[] array) { int temp; for (int i = 1; i < array.length; i++) { for (int j = i; j > 0; j--) { if (array[j] < array[j - 1]) { temp = array[j]; array[j] = array[j - 1]; array[j - 1] = temp; } } } }输出结果:[13, 24, 57, 69, 80]
7.4、希尔排序
-
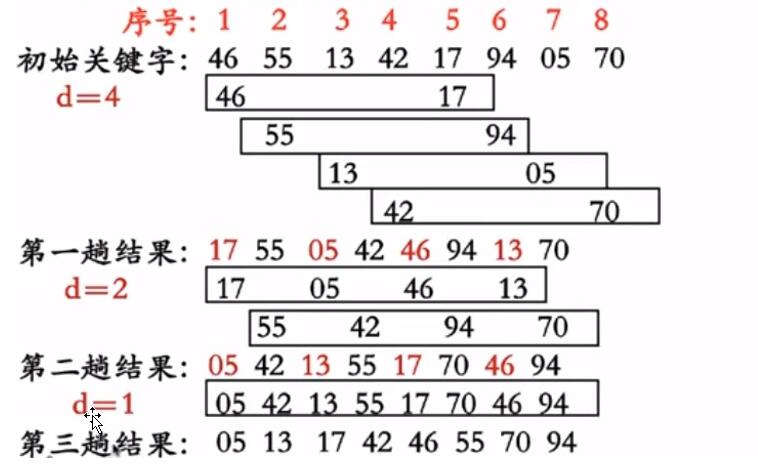
排序原理:它是对插入排序的一个优化,核心思想就是合理的选取增量,经过一轮排序后,就会让序列大致有序,然后再不断的缩小增量,进行插入排序,直到增量为1,整个排序结束。
-
图解:
-
增量的选择:
- 最普通的选择就是使用数据长度的一半,但这种增量从效率来说,不是非常好。
- 可以使用克努特序列来选择增量:h=1;h=h*3+1
-
代码实现:
public static void main(String[] args) { int[] a = {46, 55, 13, 42, 17, 94, 5, 70, 80, 90}; sort(a); System.out.println(Arrays.toString(a)); } public static void sort(int[] array) { //根据克努特序列选取我们第一次的增量 int interval = 1; while (interval <= array.length / 3) { interval = interval * 3 + 1; } int temp; for (int h = interval; h > 0; h = (h - 1) / 3) { for (int i = h; i < array.length; i++) { for (int j = i; j > h - 1; j -= h) { if (array[j] < array[j - h]) { temp = array[j]; array[j] = array[j - h]; array[j - h] = temp; } } } } }输出结果:[94, 90, 80, 70, 55, 46, 42, 17, 13, 5]
7.5、快速排序
-
算法思想:
- 分治法:比大小,在分区
- 从数组中取出一个数,作为基准数。
- 分区:将比这个数大或者等于的数全放到它的右边,小于它的数全放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
- 分治法:比大小,在分区
-
实现思路 - 挖坑填数
- 将基准数挖出形成第一个坑。
- 从后向前找比它小的数,找到后挖出次数填到前一个坑中。
- 从前向后找比它大或等于的数,找到后也挖出次数填到前一个坑中。
- 再重复执行2、3两步骤。
-
例如对5、3、9、1、6、7、2、4、0、8进行排序
元素 5 3 9 1 6 7 2 4 0 8 坑位 坑位1 坑位3 坑位5 坑位7 坑位6 坑位4 坑位2 第一轮 0 3 4 1 2 5 7 6 9 8 第二轮 0 2 1 3 4 5 6 7 9 8 第三轮 0 1 2 3 4 5 6 7 8 9 -
代码实现:
public static void main(String[] args) { int[] arr = {5, 3, 9, 1, 6, 7, 2, 4, 0, 8}; sort(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } public static void sort(int[] arr, int start, int end) { //找出分左右两区的索引位置,然后对左右两区进行递归调用 if (start < end) { int index = getIndex(arr, start, end); sort(arr, start, index - 1); sort(arr, index + 1, end); } } private static int getIndex(int[] arr, int start, int end) { //挖出第一个数作为基准数 int x = arr[start]; while (start < end) { //从后向前找比它小的数,找到后挖出此数填到前一个坑中 while (start < end && arr[end] >= x) { end--; } if (start < end) { arr[start] = arr[end]; start++; } //从前向后找比它大或等于的数,找到后也挖出此数填到前一个坑中。 while (start < end && arr[start] < x) { start++; } if (start < end) { arr[end] = arr[start]; end--; } } arr[start] = x; //把基准数填到最后一个坑中 return start; }输出结果:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
7.6、归并排序
-
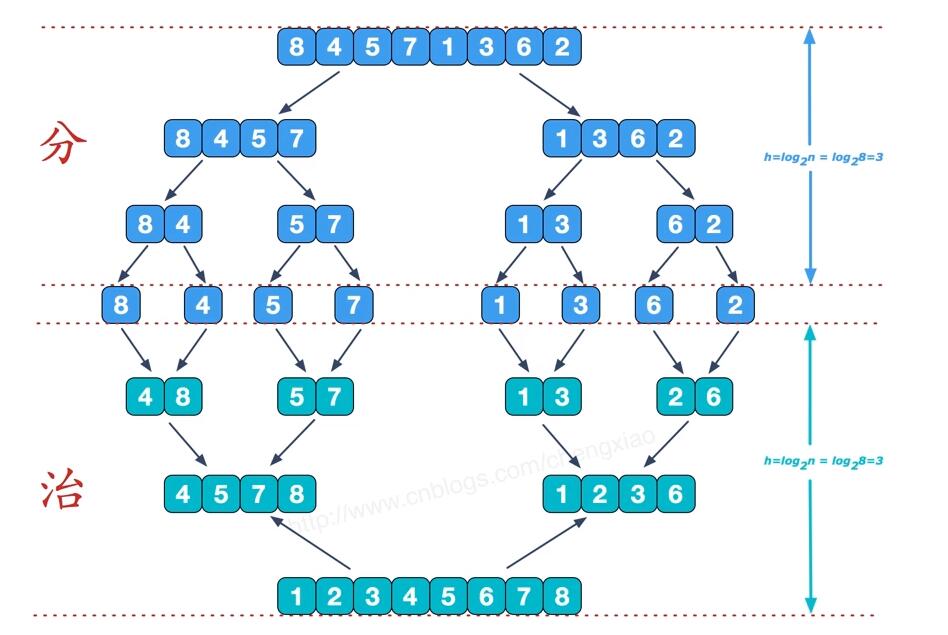
排序原理:假设初始序列有N个记录,则可以看成是N个有序的子序列,每个子序列的长度为1,然后凉凉归并,得到N/2个长度为2或者1的有序子序列,再两两归并,如此重复,直到得到一个长度为N的有序序列为止,这种排序方法称为2路归并排序。
-
图解:分而治之
-
代码实现:
public static void main(String[] args) { int[] arr = {5, 3, 9, 1, 6, 7, 2, 4, 0, 8}; sort(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } public static void sort(int[] arr, int startIndex, int endIndex) { //计算中间索引 int centerIndex = (startIndex + endIndex) / 2; if (startIndex < endIndex) { sort(arr, startIndex, centerIndex); sort(arr, centerIndex + 1, endIndex); merge(arr, startIndex, centerIndex, endIndex); } } private static void merge(int[] arr, int startIndex, int centerIndex, int endIndex) { //定义一个临时数组 int[] tempArr = new int[endIndex - startIndex + 1]; //定义左边数组的起始索引 int i = startIndex; //定义右边数组的起始索引 int j = centerIndex + 1; //定义临时数组的起始索引 int index = 0; //比较左右两个数组的元素大小,往临时数组中放 while (i <= centerIndex && j <= endIndex) { if (arr[i] <= arr[j]) { tempArr[index] = arr[i]; i++; } else { tempArr[index] = arr[j]; j++; } index++; } //处理剩余元素 while (i <= centerIndex) { tempArr[index] = arr[i]; i++; index++; } while (j <= endIndex) { tempArr[index] = arr[j]; j++; index++; } //将临时数组中的元素取到原数组中 for (int k = 0; k < tempArr.length; k++) { arr[k + startIndex] = tempArr[k]; } }输出结果:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
7.7、基数排序
-
基数排序不同于之前所介绍的各类排序,前边介绍到的排序方法或多或少都是通过使用比较和移动记录来实现排序,而基数排序的实现不需要进行对关键字的比较,只需要对关键字进行“分配”与“收集”两种操作即可完成。
-
排序实现思路:
- 先准备10个桶,下标从0 ~ 9。
- 获取数组中的最大值,来确定排序轮次。
- 从每个数的个位开始,到最大数的位结束(如百位、千位),把每个位上对应的数字与桶下标一致的元素依次放入桶中。
- 然后再按照下标顺序依次从桶中取出来排好。
- 重复3、4步骤,直到数组最大数的位结束。
-
代码实现:
public static void main(String[] args) { int[] arr = {2, 1, 5, 21, 31, 444, 23, 33, 47, 10, 903, 124, 987, 100}; sort(arr); System.out.println(Arrays.toString(arr)); } public static void sort(int[] arr) { //定义二维数组,放10个桶 int[][] tempArr = new int[10][arr.length]; //定义一个统计数组 int[] countArr = new int[10]; //获取数组中的最大值来确定排序轮次 int max = getMax(arr); int len = String.valueOf(max).length(); for (int i = 0, n = 1; i < len; i++, n *= 10) { for (int value : arr) { //获取每个位上的数字 int num = value / n % 10; tempArr[num][countArr[num]++] = value; } //取出桶中的元素 int index = 0; for (int k = 0; k < countArr.length; k++) { //判断桶中是否有元素 if (countArr[k] != 0) { for (int h = 0; h < countArr[k]; h++) { //从桶中取出元素放回原数组 arr[index] = tempArr[k][h]; index++; } countArr[k] = 0; //清除上一次统计的个数 } } } } /** * 获取数组中的最大值 * * @param arr * @return */ private static int getMax(int[] arr) { int max = arr[0]; for (int i = 1; i < arr.length; i++) { if (arr[i] > max) { max = arr[i]; } } return max; }输出结果:[1, 2, 5, 10, 21, 23, 31, 33, 47, 100, 124, 444, 903, 987]
7.8、堆排序
-
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序。
-
堆排序的基本思想:
- 将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。
- 如此反复执行,便能得到一个有序序列了。
-
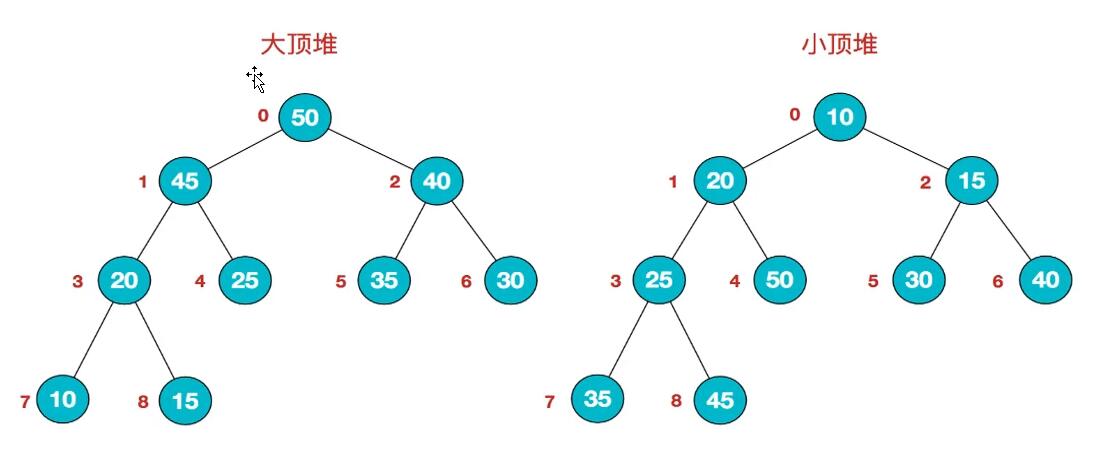
大顶堆和小顶堆
- 大顶堆的每个根节点都会大于左右两个子节点
- 小顶堆的每个根节点都会小于左右两个子节点
-
数组可以看作一个完全二叉树,数组从逻辑上讲就是一个堆结构
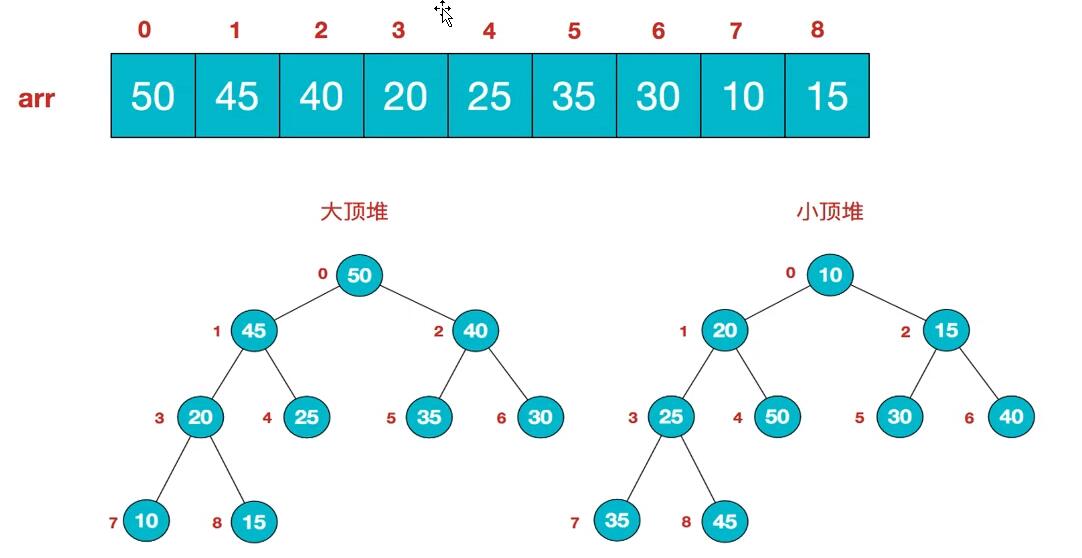
- 升序排列使用大顶堆,降序排列使用小顶堆
- 我们用简单的公式来描述一下堆的定义就是:
- 大顶堆:arr[i] >= arr[2i + 1] && arr[i] >= arr[2i+2]
- 小顶堆:arr[i] <= arr[2i + 1] && arr[i] >= arr[2i+2]
-
图解:
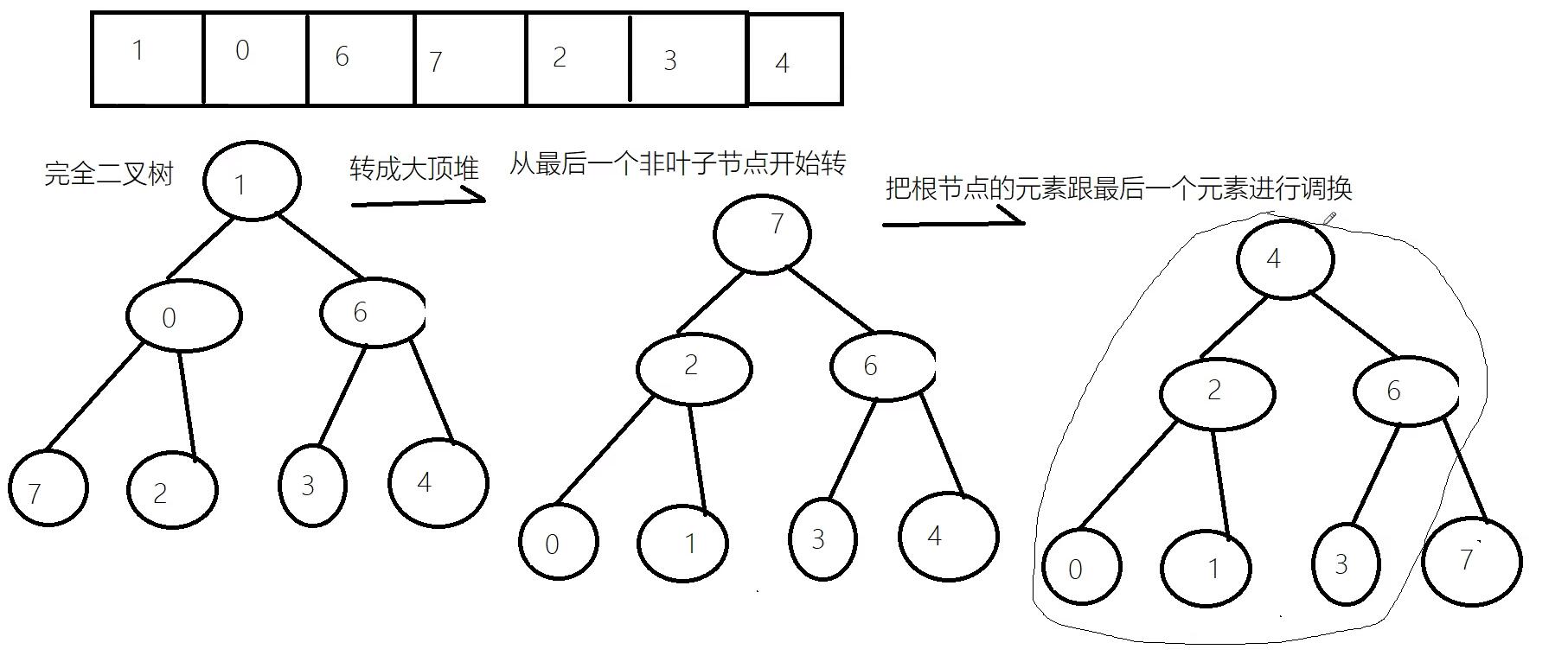
-
代码实现:
public static void main(String[] args) { int[] arr = {1, 0, 6, 7, 2, 3, 4}; sort(arr); System.out.println(Arrays.toString(arr)); } public static void sort(int[] arr) { //定义开始调整的位置 int startIndex = (arr.length - 1) / 2; //开始循环调换 for (int i = startIndex; i >= 0; i--) { toMaxHeap(arr, arr.length, i); } //经过上面的操作后,已经把数组变成了一个大顶堆,把根元素和最后一个元素进行调换 for (int len = arr.length - 1; len > 0; len--) { //进行调换 int temp = arr[0]; arr[0] = arr[len]; arr[len] = temp; //换完之后,我们再把剩余元素调成大顶堆 toMaxHeap(arr, len, 0); } } /** * 调整成大顶堆的方法 * * @param arr 待排序的数组 * @param size 调整的元素个数 * @param index 从哪里开始调整 */ private static void toMaxHeap(int[] arr, int size, int index) { //获取左右子节点的索引 int leftNodeIndex = index * 2 + 1; int rightNodeIndex = index * 2 + 2; //查找最大节点所对应的索引 int maxIndex = index; if (leftNodeIndex < size && arr[leftNodeIndex] > arr[maxIndex]) { maxIndex = leftNodeIndex; } if (rightNodeIndex < size && arr[rightNodeIndex] > arr[maxIndex]) { maxIndex = rightNodeIndex; } //我们来调换位置 if (maxIndex != index) { int temp = arr[maxIndex]; arr[maxIndex] = arr[index]; arr[index] = temp; //调换完之后,可能会影响到下面的子树不是大顶堆,我们还需要再次调换 toMaxHeap(arr, size, maxIndex); } }输出结果:[0, 1, 2, 3, 4, 6, 7]




 浙公网安备 33010602011771号
浙公网安备 33010602011771号