多项式

一个超赞的博客

快速傅里叶变换

一个写的不太好的博客

说明

在oi里的大概用途：在$O(n \log_2 n)$ 的时间复杂度内运算两个有n个项的多项式的乘积

$$C(x) = \sum_{j=0}^{2n-1} \sum_{i=0}^j a_i b_{j-i}x^j$$

多项式的乘积，x是不重要的。所以本质上解决的问题是：

$$c_k=\sum_{i=0}^ka_i \times b_{k-i}$$

也即卷积

原理

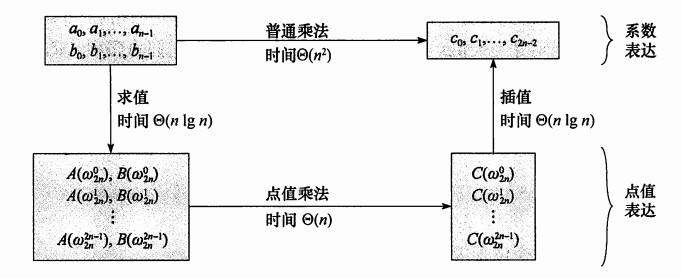
如果由系数表示直接到系数表示，复杂度是$O(n^2)$的。然而，fft通过三步转化降低了复杂度：

1. 系数表示 --> 点值表示 （dft/傅里叶变换）
2. 点值乘法运算
3. 点值表示 --> 系数表示 （idft/傅里叶逆变换/插值）

先来看第一步

第一步其实就是分别找n个合适的值带入$A(x)$,$B(x)$两个函数，使得这两个函数由系数表示法转化为点值表示法

正常情况下，这个过程是$O(n^2)$的，但是利用单位根优化可以做到$O(n \log n)$

前置内容：单位根
在复数系内，以原点为起点，以单位圆的n等分点为终点，做n个向量，设最小辐角对应的向量为$ω_n$,其余$n-1$个复数表示为$ω_n^0,ω_n^2,\dots ,ω_n^n$
则有：

1. 周期性：

$$ω_n^i=(ω_n)^i$$

1. 消去引理：

$$ω_{2n}^{2k}=ω_n^k$$

2. 折半引理：

$$ω_{n}^{k+\frac{n}{2}}=-ω_n^k$$

就不证明了，可见引用的博客

以下把n视作2的整数次幂，如果不是，就当作系数是0

设$A(x)=A_0(x)+A_1(x)$，其中：

$$A(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}$$ $$A_0(x)=a_0+a_2x+\dots+a_{n-2}x^{n/2-1}$$ $$A_1(x)=a_1+a_3x+\dots+a_{n-1}x^{n/2-1}$$

则有：

$$A(x)=A_0(x^2)+xA_1(x^2)$$

现在我们有$n$个复数了，我们把前$n/2-1$个带入（$0\leq k<n/2$）得到：

$$A(ω_n^k) = A_0(ω_{n/2}^{k})+ω_n^kA_1(ω_{n/2}^{k})$$

把$n/2$到$n-1$个带入（$n/2 \leq k' <n, k=k'-n/2$）得到：

$$A(ω_n^{k+n/2})=A_0(ω_{n/2}^{k})-ω_n^kA_1(ω_{n/2}^{k})$$

因为A的前半段与后半段函数值有简单关系，所以只要计算$A_0,A_1$的所有函数值就可以直接得到$A$的所有函数值

第二步很简单，只需要把对应函数值乘起来就好

第三步是第一步的逆过程，不想证明了，代码不需要写两份。

代码

修修滴代码，大大滴智慧~

#include <bits/stdc++.h>
using namespace std;
const int N=4e6+5;//数组要开大，因为n是变成2的整数幂了
const double PI=acos(-1);//PI的精度
char s[N];
complex<double>f[N],g[N];//定义复数类
void FFT(complex <double>*a,int n,int op){
	if(!n) return;//没有n，就是说只有第0项，是常数，答案就是系数所以直接返回
	complex<double> a0[n],a1[n];//所以空间复杂度也是log的
	for(int i=0;i<n;i++)
		a0[i]=a[i<<1],a1[i]=a[i<<1|1];//处理系数
	FFT(a0,n>>1,op); FFT(a1,n>>1,op);
	complex<double> W(cos(PI/n),sin(PI/n)*op),w(1,0);
	for(int i=0;i<n;i++,w*=W)//求值
		a[i]=a0[i]+w*a1[i],a[i+n]=a0[i]-w*a1[i];
}
int main(){
	// input()
	for(m+=n,n=1;n<=m;n<<=1);//把n变成2的整数次幂，m是得到多项式乘积的项数
  //现在是假设f和g都有n项，即最高幂次是n-1次
	FFT(f,n>>1,1); FFT(g,n>>1,1);//分别对两个函数进行傅里叶变换（函数求值）
  //现在f与g数组里存的是函数值而非系数
	for(int i=0;i<n;i++) f[i]*=g[i];//第二步，函数值乘积
	FFT(f,n>>1,-1);//傅里叶逆变换
	for(int i=0;i<=m;i++)
		printf("%.0lf ",fabs(f[i].real())/n);//除以n是为什么我不到，但是别忘了
	return 0;
}

例题

P3338 力

给出 $n$ 个数 $q_1,q_2, \dots q_n$，定义

$$E_j~=~\sum_{i = 1}^{j - 1} \frac{q_i}{(i - j)^2}~-~\sum_{i = j + 1}^{n} \frac{q_i}{(i - j)^2}$$

对 $1 \leq i \leq n$，求 $E_i$ 的值。

推式子可以得到：

$$E_i = \sum_{j=0}^i q_j \times f_{i-j} - \sum_{j=0}^{n-i} q_{i+j} \times f_j$$

其中$f_i = \frac1{i^2}$

令$q'_i=q_{n-i}~$ （逆序）
E就可以变成卷积形式了：

$$E_i = \sum_{j=0}^i q_j \times f_{i-j} - \sum_{j=0}^{n-i} q'_{n-i-j} \times f_j$$

经验总结：

1. 可以通过设置数组的方法把式子变优雅
2. 可以通过改变数组中元素顺序的方法把式子变优雅
3. sigma的起始要是0，才优雅

P3723 礼物

有两个数字环，现在把它们按任意方法对齐，把它们的对应数字做差得到一个数列，可以在这个数列的每个数上加一个同样的值，最后权值是这个数列中所有数字的和，问这个和的最小值

设已经按某种方法对其，则最终答案为：

$$\sum_{i=1}^n(a_i+b_i+c)^2=\sum (a_i^2)+\sum(b_i^2)+nc^2+2c(\sum a_i-\sum b_i)-\sum a_ib_i$$

其中要让$nc^2+2c(\sum a_i-\sum b_i)$最小可以直接公式计算，因此改变的东西只有$\sum a_ib_i$，这个东西就很卷积：

化成卷积的方法：把a数组倒序后倍长，a与b卷积后得到数组的n+1到2n位就是可能的答案。

经验总结

1. 多项式项数为定值，可以利用系数为0的特点搞

注意点

1. 数组大小
2. n/m不要搞混（尤其是最后/m的操作）

81dacd9d-fb4e-4bfd-8dbc-dd652c82d75a