做题记录

6月到11月，有效学习天数150天左右，计划做满600题，学习新东西/取得重大研究成果视其难易程度记分，黑题记30分，紫题记15分，蓝题记7分，计划集满10000分。如果达成此目标则视为胜利（ohyea），而不是在于最终结果

2024.6.2

T1 1 1 0 0 7

田忌赛1000次马，要求字典序最大

首先可以\(O(n)\)判断最多赢几轮（两个数组都排序后双指针）
逐位二分马的能力，再进行可行性判断

二分时注意对于这局是否获胜要分开二分

T2 2 1 1 0 22

平面上有5e4个点，每两个点之间有连边，线段按其与水平线的夹角的弧度排序，求中位数弧度

二分答案，对于每个点判断它上方有多少点和它的连边夹角比答案小，即在这个点画一条当前斜率的线，有多少点在你右上方，可以把所有直线投影到x轴上，树状数组维护

2024.6.3

T3 3 1 1 1 52

n * n 网格，中间有2n个垃圾，每行第0个位置和每列第0个位置有机器人，机器人收回该列/行最近的垃圾后就消失，问收完所有垃圾的派机器人的排列方案数

二分图建图，边代表垃圾，点代表机器人，则一个连通块中，如果边数与点数不等，则一定无解。否则边数与点数相等，整个图是一个基环树森林。

现在我们要把每条边分给一个点，即点与边一一对应。考虑树中一定是边分给儿子，环只有顺时针/逆时针两种情况。

考虑一种特定的分配方案，其排列方案数如何计算。考虑在选择每个点时，其前置条件是哪些节点。其实就是原图中，与你相连的所有节点中，所有比你要收回的那条边对应的节点编号小的。

按照这样的前置条件建图，是一个森林。现在问题变为求森林拓扑序数

这里来了一个trick：森林的拓扑序数为\(\Large{\frac{n}{\Pi sz_u}}\)。证明：dp式子削一下

卡常：反复调用的函数用inline、用int代替longlong、最重要的是少用STL，手写栈和集合

T4 4 2 1 1 59

给定图，在图的基础上对于每个点，如果有两个与它相连的点编号都比他大，二者连边。相邻的点颜色必须不同，有n中颜色，问染色方案

考虑从编号最大的点开始染色，则每个点的染色方案数是\(n-siz_u\)，其中siz是与u相邻且编号比u大的点的个数（因为这些点显然颜色都不相同）

如何统计【与u相邻且编号比u大的点的个数】？启发式合并
两个vector/set交换复杂度\(O(1)\)

点分治(类邻域) 5 2 2 1 74

2024.6.4

虚树 6 2 3 1 89

oiwiki讲的已经足够清楚了
解决问题：如果我们当前求的东西只考虑树上某些关键点的问题，那么可以把这些点和它们所有的LCA拎出来（这就是虚树），然后再DP求解，复杂度可以做到\(O(m \log n)\)
主要流程：

1. 预处理DFN序，祖先信息
2. 把关键点按DFN序排序
3. 把相邻的关键点的LCA都求出来（这就是所有关键点的LCA了）
4. 把所有关键点和它们的LCA按DFN序排序
5. 把相邻的点和它们的LCA连边（设编号为x、y，则连接（lca(x,y),y)）

CF1608 推牌九 7 3 3 1 96

考虑状态数不多，且【前后相邻】这个条件比较像连边，所以考虑建立转移图，得出结论WW和BB总数相同，因此W和B的总数也相同。所以充要条件就是把部分?分给W，使得W个数恰好为n

CF1975 8 4 3 1 116

E题：考虑你每次更新儿子太慢了，只能想办法更新父亲。
类似差分，把你染成黑色就给你加一并且给你父亲减一
合法情况有两种，一种是1、-1各有一个，另一种是各有两个且相邻且恰好有一个是黑色的
这第二种咋判断？
set的插入删除是近似O(1)的\

2024.6.5

P4103 虚树 9 4 4 1 131

P3233 虚树+DP比较难 10 4 5 1 146

每次给定m个关键点，每个点会去离他最近的一个关键点，询问每个关键点有多少个点来。

首先建立虚树。考虑虚树上不是关键点的点，它的贡献全部算给离他最近的关键点。虚树上的点的非虚树子树，贡献一定算给这个节点。最麻烦的就是这种情况：

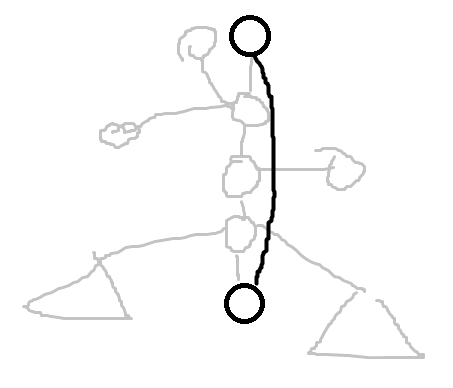
但是也容易维护。处理出上下两个节点最近的关键点的距离，从而计算链上给上下两个节点的分界点在哪。

P2261 数论分块 11 5 5 1 153

数论分块可以在\(O(\sqrt{n})\)的时间复杂度内计算\(\sum_{i=1}^{n} f(i) \cdot \lfloor \frac{n}{i} \rfloor\)
因为\(\forall 1 \leq i \leq n\)，\(\lfloor \frac{n}{i} \rfloor\) 的不同取值个数为\(2\sqrt{n}\)
对于\(i=x\)，若要求\(\lfloor \frac{n}{i} \rfloor = \lfloor \frac{n}{x} \rfloor\)，则i的最大取值为\(i = \lfloor \frac{n}{ \lfloor \frac{n}{i} \rfloor } \rfloor\)

	int l=1,r;
	while(l<=n){
		r = min(n/(n/l),n);
		/*some operations*/
		l = r+1;
	}

CF1954E 数论分块 12 6 5 1 160

莫队（简单） 13 7 5 1 167

操作序列分块(好题) 14 7 6 1 182

给定一棵树。初始只有节点1是红色的。m次操作，把一个节点染成红色，或查询一个节点到与其最近的红色节点的距离。

操作序列分块，bfs所有点到红色点的距离/查询每个红色点到你的距离

dsu on tree(easy) 15 7 7 1 197

2024.6.9

P4437(贪心 排序) 16 7 8 1 202

给定一棵有权树，要求父亲比子孙先选，求\(\sum i\times w_{p[i]}\) 的最大值

考虑全局权值最小的节点。选完他的父亲后必然第一个选择他。故将这个节点与他的父亲合并。
合并后又出现现在权值最小的点，一定又要和他的父亲合并。
这样一直合并下去，显然会出现需要判断序列和序列之间的大小关系的情况。

这个就列式子，假定两个序列的先后顺序，得到第一个序列比第二个优的充要条件

分层图 17 8 8 1 209

fibonacci 18 9 8 1 216

fib前两项已知，可以通过预处理的值推算某项的值与前缀和

CF145E 19 10 8 1 223

DP+分治(好题) 20 10 9 1 238

给定序列a，把它分成k段，每段代价为数值相同的数字对数。问最小代价和

设\(f[i][j]\)表示前j个位置分成i段的最小代价。则\(f[i][j] = \min(f[i-1][k-1]+cal(k,j))\)
首先枚举i，之后对于j，这样具有决策单调性。
考虑分治，若要计算\(ql \le j \le qr\)的所有dp值，先计算\(j = (ql+qr)/2\)的dp值，保存其决策位置，然后递归\([ql,j-1]\)和\([j+1,qr]\)求解。
如何快速计算cal()的值。考虑莫队思想。

2024.6.10 模拟赛

开T1，不到10分钟看出是字典树，开赛20min写完，检查10min，发现字典树son[]数组开小了
开T2，思考半小时得到细致思路，写+调了一个小时，因为这题细节很多，检查了半个小时，检查过程中也发现一些小错误
开T3，是数论题，不会。打表，打了部分分32pts。花了半个小时。由于所剩时间不多，没检查
开T4，是树，我擅长的。打了68分暴力（结果冲过了89。），比赛时间还剩40分钟。发现T4是动态dp几乎板子的题，但是一时间列不错矩阵。感觉应该写不了正解了，就转看T3
研究T3性质研究到比赛结束也没啥结果
T3由于忘记取模挂到12分了

预计分数：[100+100+32+68]
实际分数：[100+100+12+89]
排名：2

果然还是要部分分+检查不能贪多。
这次状态很不错。以后保持策略。

问题总结：

1. 没取模。这个是记录在常犯错误中的一条，应该在比赛结束前十分钟再把每个常犯错误过一遍

T1 字典树 21 11 9 1 245

T2 基环树 DP 22 11 10 1 260

T3 arc015f GCD fibonacci 23 11 10 2 290

T4 动态DP 24 11 11 2 305

2024.6.11

CF508D 欧拉路径 25 12 11 2 312

\(O(n)\)寻找欧拉路径：
寻找起点。若所有点的入度与出度相同，则随便找一个点；否则找到入度比出度大1的点作为起点。
DFS。边dfs边删边

void dfs(int u){
	for(int i=h[u];i;i=h[u]){//为什么这个i=h[u]，因为在递归的过程中很可能ne[i]已经死了
		h[u] = ne[i];
		dfs(to[i]);
	}
	ans[++top] = u;
}

对于这道题，把每个连续的两个字母看作一个点，每个条件就相当于在两个点之间连边（把条件看作边），转化为需要找到一条欧拉路径

CF840D 主席树 trick 26 12 12 2 327

给定序列a，每次询问一个区间和一个k，问满足\(cnt_x > \frac{r-l+1}{k}\)的最小的数x

主席树只能维护和不能维护最值呀
主席树就像是把你任何子段排序
设\(d = \frac{r-l+1}{k}\)，排序后每隔d个询问个数，则答案一定在这些询问之中。

也可以考虑另一种思路，只要权值区间的数字个数总和比 d 大，就递归查找。这样的复杂度也是\(O(nk \log n)\)的，常数还更小。

CF1375E trick 27 12 13 2 342

给定一个长度为 \(n\) 的序列 \(a\)，求 \(a\) 中的所有逆序对 \((i_1, j_1), (i_2, j_2), \cdots, (i_m, j_m)\) 的一个排列 \(p\)，使得依次交换 \((a_{i_{p_1}}, a_{j_{p_1}}), (a_{i_{p_2}}, a_{j_{p_2}}), \cdots, (a_{i_{p_m}}, a_{j_{p_m}})\) 后序列单调不降。
\(1 \le n \le 10^3\)，\(1 \le a_i \le 10^9\)。

缩小规模：首先考虑一个排列怎么做。可以先通过一些操作使得最大的放到最后，且前面的相对大小关系不发生改变。

排列 -> 可重 可以以数值为第一关键字，位置为第二关键字，强行转成一个排列，这样对逆序对不产生影响，也不影响结果。

CF911G 动态开点线段树 28 12 14 2 357

给出一个数列,有q个操作,每种操作是把区间[l,r]中等于x的数改成y.输出q步操作完的数列.
\(a_i \le 100\) \(n,q \le 2\times 10^5\)

线段树维护每个值变成的值，复杂度\(O(nm \log n)\)可以冲过去

开m棵线段树，维护每个权值的位置，更新时进行线段树的分裂与合并

复杂度分析：正常情况下单次操作复杂度不超过\(O(\log n)\)，但如果转移的两棵线段树对应子树都有的话，复杂度可能出问题。然而，如果要形成上述情况，就需要执行相应的低复杂度操作，均摊下来复杂度仍然正确。

CF1559D2 贪心 29 13 14 2 364

给你两棵森林，节点数均为 \(n\)。
允许你进行加边操作，但是有两个要求：

• 如果在第一个森林加一条 \((u,v)\) 的边，第二个森林也要进行同样的操作。反之同理。
• 加边后两个森林依旧是森林。（一棵树也是森林）

求最多能加几条边，并输出加边方案。

因为加一条边最多只会对一条边的加入产生影响，所以可以贪心，能加就加

考虑对于一个节点x，枚举所有节点y，判断是否可以加入边(x,y)

对于无法加入的节点y，可以分成三类

• 在图1和图2都和节点x有连边
• 图1有，图2无
• 图1无，图2有

对于第一种情况，考虑这个点肯定没办法和x连边了。对于剩下的点，也肯定在某个图与x有连边，所以如果节点y和剩下的节点连边，就必然产生环。
对于第二三种情况，肯定不能和自己一样的情况连边，否则也会产生环。所以只能这两种之间连边。

2024.6.12

CF1305F gcd 随机化 30 13 15 2 379

给定 \(n\) 个数。每次可以选择将一个数 \(+1\) 或 \(-1\) 。求至少多少次操作使得整个序列都是正数且全部元素的 \(\gcd>1\) 。
\(n\leq 2\times10^5,a_i\leq 10^{12}\) 。

首先考虑一个好下手的情况，就是gcd=2。这种情况下答案为奇数的个数，这是答案的一个上界。

做法1：随机化
我们注意到存在一半以上的数变化量\(\le 1\) ，所以选择一个数，假设它的变化量\(\le 1\) ，对\(a_i\)、\(a_i-1\)、\(a_i+1\)质因数分解，质因子是可能的答案。这个操作重复T次，失败概率为\(\frac{1}{2^T}\)

做法2：
设奇数个数为\(t\)，注意到每个数的最终取值范围都在 \([ a_i-t , a_i+t ]\) 。因此可以任意找一个 \(a_i\)，对于它的每种最终取值，对它质因数分解，得到若干可能的答案。对这些答案一一尝试即可。

关于复杂度：经常可以设一个阈值，小于阈值的有一个复杂度，大于的也有一个
例如：\(\sum_{i=1}^{n} \frac{n}{i}\) 的总和规模是\(n \sqrt{n}\)

CF468C 构造 31 13 16 2 394

CF1043F gcd 32 13 17 2 409

与CF449D有异曲同工之妙
多个数的gcd可以类比二进制数的与操作

CF449C 类gcd trick 33 13 18 2 424

【质数的倍数】很奇妙。
好像是典题。

今天做到的题为啥都是稀奇古怪gcd /yun

CF986C 位运算 34 13 19 2 439

给定m个\(2^22\)以内的数，对于按位与和为0的点对连边。问连通块个数

x、y与和为0 <==> (~x)包含y
dfs遍历子集

2024.6.13 JOI 2022 Final

前两个题很简单，总共用了20min+30min做完+检查
第三题思路稍微偏了一些，在错误的道路上想了40min无果。只能打暴力跑路。其实思路离正解很近，就是想不到。可能再给我半个小时也想不出来。这只能靠多练习解决吧，赛场只能果断放弃。
第四题花了一个多小时明确思路，不到一个小时实现。在结束前10分钟调出来
最后没挂分ohyea

唯一问题在于T3暴力没打满。如果想优化做题效率，T3发现偏离应该及时跳题，千万别浪费时间。

期望得分 = 实际得分 = [100+100+33+100]

T3 贪心 DP 35 14 19 2 446

翻译太难了.jpg

一开始想到按\(a_i\)排序后进行DP，然而只能列出\(O(mn^3)\)的做法

其实\(a_i\)的前后顺序重要程度不如\(b_i\)，因为按从小到大的顺序选取\(b_i\)后，\(a_i\)的选取顺序无关。所以按\(b_i\)从小到大排序，发现所有选出的b前面只可能存在选a或选b，不可能存在不选。因此可以DP求解。

T4 倍增 RMQ 36 14 20 2 461

大好题

长度为n的铁路上有m个有向区间作为火车线路。可以上火车当且仅当离始发站距离小于K，q组询问，问从一个点去另一个点的最小换乘次数。

这种类似于在不同层的线段上跳跃的问题可以想到倍增。
相当于前(1<<j-1)步你可以跳到的区间范围是[l,r]，那么前(1<<j)步可以跳到的范围就是[chkmin[l,r],chkmax[l,r]]
统计答案过程类似于倍增求LCA

CF484E 37 14 21 2 476

给定一个长度为n的数组a，每次询问给定一个区间[l,r]和一个值k，问区间[l,r]的所有长度为k的子区间的最小值的最大值

将复杂数组转化为01数组，与那个排序题类似
二分答案，大于等于答案的都设为1，小于答案的都设为0，相当于判断是否有长度为k的全1区间。这个可以离散化后主席树维护。
主席树尽量每个版本只修改一个值好么。如果要修改多个值，考虑这样做：

idx++;
if(u) tr[idx] = tr[u];
else tr[idx] = tr[v];
u = idx;

CF1100F 38 14 22 2 491

给定长度为n的数组a，每次询问给定区间[l,r]，问 \(a_l 到 a_r\) 中任选若干个数，异或和的最大值是多少。

最大异或和考虑线性基
区间最大异或和考虑前缀线性基
这个东西就是，你希望你线性基离的元素是靠后的位置贡献的，所以不断用靠后的替换靠前的，得到最优的线性基。

CF1527E 线段树优化dp 分治决策单调性dp 39 14 23 2 506

由于套路之前全见过了。

对于【分治决策单调性】，和6.9做过的CF868F很像。

2024.6.14

CF348C 根号分治 40 14 24 2 521

好题。
给定一个n个数的序列a，m个下标集合，记\(S_{k}=\{S_{k,i}\}\)。
两种操作：

1. ? k 求集合k的和，即求集合k 所有元素做原数组下标的和
2. + k w 给集合k的所有下标代表的数加w。
   \(n,m,q,\sum siz_{S_i} \le 10^5\)

把集合分为重集合与轻集合，对于重集合打标记，对于轻集合暴力修改，对于所有集合维护它们与重集合的关联。因为重集合数量少

CF321E 分治决策单调性DP 41 14 25 2 536

又来

2024.6.16

CF622F 拉格朗日插值 42 14 26 2 551

求\(\sum_{i=1}^n i^k\)，其中\(n\le 10^{15},k\le 10^6\)

k次多项式的前缀和显然是k+1次多项式，因为\(x^k\)是关于\(x\)的\(k\)次多项式，所以\(\sum_{i=1}^n i^k\)是关于\(n\)的\(k+1\)次多项式
故可以拉格朗日插值解决

CF3D 括号匹配 43 15 26 2 558

CF940F 带修改莫队 44 15 27 2 573

带修改莫队，需要将时间也作为一个维度。设n与m同阶，设置块的大小为\(n^{\frac{2}{3}}\)较为合适。最终复杂度在\(3 \times 10^8\)左右
因为其时间复杂度较大，不能在修改过程中增加任何较大的常数。要尽量多地预处理，在修改之外处理东西
这个容易写错，要写拍子呀。

P4074 树上莫队 45 15 28 2 588

树上莫队分为两种

一. 括号序列树上莫队
按dfs序遍历，进入时标记一次，子树遍历完以后再标记一次，记录每个节点第一次被遍历时在序列上的位置为\(in[u]\)，则对于一条路径\((u,v)\)，其对应的操作区间就是\([in[u],in[v]]\)，其中出现两次的节点就当作没出现。
需要注意的一点是，当u!=lca(u,v)时，需要特判u和lca(u,v)

二. 树上分块树上莫队
类似于王室联邦的操作，像区间一样的对询问排序，然后暴力移动节点u，v即可。

2024.6.17

P5906 回滚莫队 46 15 29 2 603

有些操作只能单个加入，很难单个删除，这就用回滚莫队。
排序后，对于L在同一个块里的询问，显然R是单增的，而L可能会在块内反复横跳。所以我们每次向右拓展R，对于L从块的右端点开始拓展。

CF547D 二分图 欧拉回路 47 15 30 2 618

给定 \(n\) 个整点，你要给每个点染成红色或蓝色，要求同一水平线或垂直线上两种颜色的数量最多相差 \(1\)。
\(n,x_i, y_i \le 2 \times 10^5\)。

方法1：
整点配对无脑二分图
对于度数为奇数的点连向一个虚拟节点
现在所有点的度数都是偶数
跑欧拉回路，则每个点有一半边是入边，另一半是出边
将右部点指向左部点的边作为一种颜色，左部点指向右部点的边作为另一种颜色
因为每个点连向的边全部是另一边的点，所以构造正确。
另外欧拉回路有个更好的写法

void dfs(int u){
	for(int &i=h[u];~i;i=ne[i]){
		if(vis[i]) continue;
		vis[i]=vis[i^1]=1;
		ans[id[i]] = i&1;
		dfs(to[i]);
		return;
	}
}

方法二：
同一行或同一列的点都两两匹配连边，形成一些短链和长度为4的环，对图进行黑白染色即可。

CF741C 构造 二分图 48 16 30 2 625

有2n个人围成一圈坐在桌子边上，每个人占据一个位子，对应这2n个人是n对情侣，要求情侣不能吃同一种食物，并且桌子上相邻的三个人的食物必须有两个人是不同的，只有两种食物（1或者是2），问一种可行分配方式。

构造题有时候条件限制较松，应该自己约束
对于这道题，在相邻两个点之间连边，这样每个点的度数恰好为2，形成的必然是若干个简单环。又因为每个点只能连一条到不相邻点的边，所以是若干个偶环
对于这种连边染异色的图，全是偶环再好不过了

CF631E 斜率优化DP 49 16 31 2 640

CF1208F 高维前缀和 贪心 50 16 32 2 655

给定 \(n\) 个数的数组 \(d\)，找到 $i\lt j\lt k $ 的 \(i,j,k\)，使得 \(d_i|(d_j \& d_k)\) 最大

按位贪心，然后可行性判断
考虑枚举哪部分由\(d_i\)包含，哪部分由\(d_j \& d_k\)包含
对于由\(d_j \& d_k\)包含的部分，考虑维护最靠后的位置和次靠后的位置。

arc177_d 51 16 33 2 670

逆元可能出现0的情况会出问题，所以还是少用逆元，写个线段树。。。

2024.6.18

arc177_e 52 16 34 2 685

CF6D DP 53 17 34 2 692

CF1375F 交互 构造 54 17 35 2 707

CF1416D 并查集 55 17 36 2 722

发现不管是倒序还是正序都没法做
那就既倒序又正序
先倒序跑出重构树，对于块的合并操作，新建一个点，把要合并的两棵树接在这个点下面
然后一个连通块就是一棵子树。

CF1325 56 17 37 2 737

给一些数，每个的因数个数不超过7，求最少选出多少个，使得乘积为完全平方。无解输出−1。

考虑限制条件，发现一个数最多有两个不同的质因子。可以先把平方因子都除去，剩下可能是两个质因子的乘积，也可能是一个质数。前者可以用质数之间的连边来刻画，则相当于要找最小环；后者可以将这个质数与1连边，也可以把它视作线段的端点，相当于找最短线段。这可以bfs解决。

对于【找最小环】这个操作，tarjan是不行的。可以使用\(O(nm)\)的bfs，也可以用\(O(n^3)\)的floyd。此处由于点、边都不满，可以使用前者，枚举每个点作为最小环上的点。

2024.6.19

CF527E 欧拉回路 57 17 38 2 752

欧拉回路删边，但是如果初始化h[]数组为-1，可能会因为【在二次遍历时改为-1】从而导致下标为负数。

CF240F 线段树 58 17 39 2 767

抓住颜色种类少的特点，开26棵线段树。

CF1278F 期望 斯特林数 数学59 17 40 2 782

P1337 模拟退火 60 18 40 2 789

搞笑了，快上高二了模拟退火还不会。

P2503 模拟退火 61 19 40 2 796

2024.6.20

矩阵快速幂 62 20 40 2 803

数论分块 63 20 41 2 818

出现\(\sum \lfloor \frac{x}{a_i} \times (a_i-1) \rfloor\)的形式，想到数论分块。

线段树 64 20 42 2 833

一个 k * k 剧场，每次购买一排长度为\(m_i\)的座位，使得这排座位中每个位置到剧场中心的距离之和最小，问每次选择座位的位置

首先选购方案可以分为两种，一种是在上方或下方选择靠近中心的一排，另一种是在左边或右边贴着已经选过的选一排。前者是好维护的，后者可以转化为求 长度大于等于选购长度 且端点距离中心位置最近的区间。这相当于在一段区间长度的后缀中找距离最小值，可以线段树维护。
但是同一长度可能出现多个位置怎么处理？考虑把线段树的叶子节点建成优先队列。

CF2C 计算几何 65 20 43 2 848

虽然这是一道蓝题，但这是因为有模拟退火的做法。计算几何还是非常麻烦的。

CF1515F 构造 66 21 44 2 863

首先猜一个结论：有解的充要条件是，\(sum \geq (n-1)\times x\)
这个结论的必要性显然
对于充分性，考虑对于有解的情况，构造一组解
发现这个条件对于边没有限制，也就是说对于一棵树，也一定要有解。（树的限制强于图）
因此考虑对于一棵树构造解。
每条边都要缩起来。
从下往上推，如果儿子大于x，则直接缩起来，父亲权值增加
上面这一步做完之后，所有儿子都小于x，那根一定巨大，所以从根往下推

CF1344C 构造 67 21 45 2 878

CF1439C 线段树 二分 68 22 45 2 885

当遇到【二分 -> 线段树查询】的问题，可以直接在线段树上二分。
比如从一个位置开始的和

CF13E 分块 69 22 46 2 900

CF455D 分块 70 22 47 2 915

每个块用一个deque

2024.6.23 模拟赛

状态一般，尤其是模拟赛出的 像屎一样 就是说屎，吃完屎状态更差了

T1是屎，题目没有说清楚梯形是否可以旋转，以为可以，盯了好一会，得出结论，做不了一点。

T2是屎，试图写一种正确做法，只会\(O(n^2)\)，写了俩小时。然后可以过样例，预计有70pts

T3是后缀自动机我不会啊，然后忘了SG函数怎么弄，导致想了半小时一点分都拿不到

T4是欧拉序，我不会啊，\(O(n^2)\)暴力巨难写，写了120多行，写的自己都不想看的那种，懒得调了。

还有40min，回去看看T1吧，装作T1是水平的。写了个。

T1确实是水平的，但是好像写错了。挂到50pts。T2题目是错的，我考虑的还稍微全面一点，得到70分。T3没写0分。T4也0分。

预计分数：[100+70+0+30]
实际分数：[50+70+0+0]
排名：4/10

1. 从好写的部分分开始写啊，别上来就写麻烦的
2. 早饭虽然不能吃多，但也别吃太少啊，后面都低血糖了
3. 知识面再拓宽一点啊，感觉最近比赛波动幅度很大的原因就在于 挂分+碰知识点

6.24

CF1592D 欧拉序列 71 23 47 2 922

三种把树压平的序列：

• dfs序 特点：每个点只出现一次，子树化为区间
• 欧拉序1 特点：相邻的位置在树上有边
• 欧拉序2 特点：括号匹配

欧拉序列有道题不会做啊this one

CF383E 高维前缀和 72 23 48 2 937

CF932F dp 李超线段树 73 23 49 2 952

有一棵树，每个点有两个权值\(a_i,b_i\)，从u跳到一个子孙v花费代价为\(a_u \times b_v\)，问从每个点跳到叶子节点的最小代价

有dp转移方程：\(f_u = min \{ f_v + b_v \times a_u \}\)。看到这个式子能够想到斜率优化，但是动态凸包这是个非常恐怖的事情，非常麻烦，所以考虑换一种思路

把\(b_v\)看作斜率，\(f_v\)看作截距，于是成为一条直线，dp转移相当于找横坐标为\(a_u\)的纵坐标最小值，考虑李超线段树。

CF1270G 构造 74 23 50 2 967

建图。

6.25-26 后缀自动机 81 23 56 3 1127

见串串

7.1

P1117 82 23 57 3 1142

拆分出AABB的形式，有多少拆分方式

先求出AA形式的串，记录a[i]表示以i结尾的AA串有多少，b[i]表示起始位置为i的AA串有多少，答案可以计算。
枚举AA串中A的长度，每A个位置设置一个关键点，找到相邻关键点的lcs和lcp（这个用SA），这一对相邻的关键点对ab数组就形成一个贡献区间。

在cdjx集训ing

P2463 SA 83 23 58 3 1157

其实就是找差分数组的最大公共子串，可以把所有串拼起来，然后二分答案，可行性判断就是连续的height比答案大，是否涵盖了所有串

P2336 SA 84 23 59 3 1172

求每个名字被点了多少次，以及每次点名有多少人被点到，点名定义为点名串为名字串的子串

把名字串接成一个串，则每个点名串对应名字串SA上的一段区间。莫队求解

P2178 SA 85 23 60 3 1187

两个相等的子串形成一对匹配，问对于每个长度，有多少对匹配，以及匹配中权值乘积的最大值

可以枚举断点，前缀和优化

P3649 SA 86 23 61 3 1202

找出串的一个回文子串使得其长度与出现次数的乘积最大

manacher + sa，统计出现次数时，先找到该位置对应的sa位置，再倍增找第一个、最后一个height

oifc 7.1 87 23 62 3 1217

给你一个长度为 n 的排列，你需要进行若干次操作：每次你可以交换位置相邻的两个元素，要求这两个元素之差大于 1 ，问最终可以得到多少个不同的排列、从初始排列到所有排列的距离之和是多少

这个限制相当于在相差为1的元素之间连有向边，第一问相当于问图的拓扑序个数。这个可以设dp状态\(f[i][j]\)表示考虑前i个数，最后一个相对位置为j，方案数是多少

考虑距离这个东西其实就是按原序列位置从1到n排序后，最终序列的逆序对有多少。
也就是说，对于每个位置，我们要看有多少位置比你大，但是最终在你前面。我们可以钦定这个位置
设\(f[i][j][k]\)表示前i个数，钦定位置的相对位置为j，最后一个位置的相对位置为k，方案数有多少。对应地，设\(g[i][j]\)表示前i个数，位置i的相对位置为j，所有方案的逆序对之和。
g的转移：先不考虑最后一个位置对答案的贡献，容易转移。然后加上最后一个位置的贡献，考虑对于f函数，哪些状态会对当前位置的逆序对产生贡献。当然是钦定位置与最后位置的相对位置反过来的时候啦。

oifc 7.4 交互 构造 88 23 63 3 1232

一个01序列，每次问一个集合，返回0多、1多还是一样多。可以翻转一个区间。以最少询问次数得到序列中有多少1

oifc 7.5 字典树合并 89 23 63 4 1262

给定n个字符串，求\(\sum_i \sum_j^{j \ne i} LCP(i,j) \times LCS(i,j)\)

放到字典树上考虑，前缀可以直接看lca深度。对于后缀，需要把不同子树的反串的字典树建出来求解。这太不牛了，考虑通过字典树合并来优化这一操作。原式可化为\(\sum_k \sum_i \sum_j LCP(i,j) \times [LCS(i,j) \ge k]\)。

oifc 7.7 90 24 63 4 1269

肯定有一个位置t是0，设\(f[i][j]\)表示走j步到达i最小代价，最后只需要求\(\min(f[u][i]) * \min(g[u][i])\)

oifc 7.10 点分治优化建图 91 24 63 5 1299

10组数据，每组数据给定一n（n<=1e5）个节点的棵树，以及10个询问，每个询问给出起点s和路径长度a，要求从起点出发，每次恰好走长度为a的路径，要求对于每个节点输出从起点到这个节点最少走多少次。

考虑把所有长度为a的路径两个端点之间建边，可是这样会建出\(n^2\)条边。所以考虑优化建图。考虑长链剖分，然后跑dsu on tree。具体来讲，对于每个节点，建立两个新点，表示入点和出点，与该节点建边权为0的边。dsu时，每加入一棵子树，找出对应深度对应的入点和出点，与原先的入点和出点之间建边，使得对应深度之和为a。然后对于同一深度的对应入点和出点，建立新的入点和出点，相当于合并了两棵子树的信息。时间复杂度\(O(n)\)

7.17

CF715C dsu 92 24 64 5 1314

给定一棵树，树上一条有向路径的权值是将边权的数组挨个写成一串数。问有多少路径满足其权值模【给定模数】得0。

推出和u v lca 有关的条件成立时的式子，然后把只和当前节点有关的部分提出来，得到【只和当前节点有关】=【只和lca与另一个节点有关】的式子，正反两个方向都这么做。dsu的时候，一个子树一个子树的查询然后更新，查询一个端点在前面子树，另一个端点在当前子树的，正反两个方向的的路径。

逆元：扩欧

CF1634F 差分 93 24 65 5 1329

给定等长的序列A和序列B，每次一个区间，表示把序列A或者序列B的对应位置加上一段fib数列，问修改后两个序列是否相等。

问两个序列是否相等，可以考虑设序列C，使得\(C_i = A_i - B_i\)，要求相当于C全0。加上fib序列这个东西很棘手，如果是加定值可以考虑差分，加fib可以考虑设置\(D_i = C_i - C_{i-1} - C_{i-2}\)。因为这样，对于中间一个位置，其\(D_i\)值不会发生改变。只有开头和结尾的会改变。

CF1601D 排序 94 24 66 5 1344

感觉还是太难想到了。

7.18

CF452F 哈希(线段树维护) 95 24 67 5 1359

给你一个1到n的排列，你需要判断该排列内部是否存在一个3个元素的子序列(可以不连续)，使得这个子序列是等差序列。

首先并不是说足够长的排列一定有这个东西的。

则问题相当于要找一个a[i]，使得其两边的数字分布不是回文的。

用哈希维护回文串，在某一位置更新时，用线段树，线段树中，一段区间表示的是这段区间的哈希值。

CF1572C 区间DP 96 24 68 5 1374

7.19

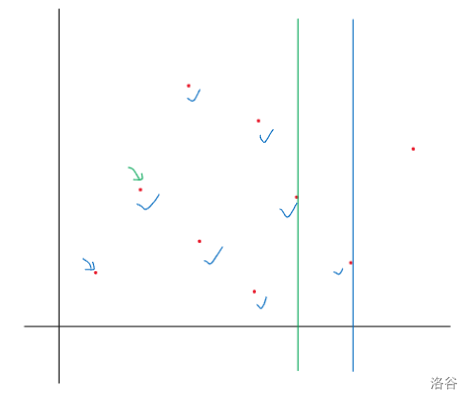
CF293E 点分治 类似P4178 97 24 69 5 1389

路径长度有两个关键字，求两个关键字都满足要求的路径总数

无脑点分治啊，然后是一个类似二维数点的问题。考虑不是很好一个子树一个子树的更新，所以考虑容斥，即所有路径减去起点终点在相同子树中的路径。所有路径怎么做，即考虑贪心，以第一关键字排序，对于每个左部点，找最大的右部点，则能与左部点匹配的是从左部点到右部点的区间。剩下一维用树状数组解决。

CF605E 期望 98 24 70 5 1404

\(n\) 个点的有向完全图中， \(i \to j\) 的边每天出现的概率均为 \(p_{i,j}\)，若 \(i = j\)，有 \(p_{i,j} = 1\)。每一步可以走到一个出现的边的点或者不动。 求最优策略下从 \(1\) 到 \(n\) 的期望天数。

考虑如果一个点只有一条转移路径怎么做。是那个模型。多个也可以列出式子。
如果比当前节点劣的节点，那就算不动也不会走过去。对于比当前节点优的节点，需要按照从优秀到不优秀排序。这个用类似dijkstra算法的东西，从后往前推。

CF1856E2 bitset 99 24 71 5 1419

一些数字，分为两部分，使得两部分的数字和之差最小这个问题本来是很难搞的，但如果值域总和小，可以01背包，复杂度\(O(n^2)\)。如果硬做，可以用bitset压位。

手写bitset笔记

CF1364E 交互 构造 随机化 100 24 72 5 1424

考虑确定一个位置的值时，其实不必要把所有的其他位置都遍历一遍。只要遍历15个，这样答案出错的概率为到不了\(121 \times 2^{-15}\)，也太低了。
最后算下来询问次数即使超过要求了，但是跑满的概率，也太低了。实在不行把数组shuffle一下。

7.20

CF444C 线段树 101 25 72 5 1431

势能分析，然后感觉很对。证明太难了。

CF1051F tarjan 最短路 102 26 72 5 1438

【关键点】

7.21

CF961G 斯特林数 103 26 72 6 1468

给定n个球权值，将这些球放到k个盒子里，盒子不能空，每个球的贡献是本身权值 × 所在盒子中球的个数，求所有划分方案的权值和

考虑拆贡献，把贡献拆到每个球上，可以列出式子

\[ans = \sum_{i=1}^n w_i \sum_{S=1}^n s \times \Big( \begin{matrix} n-1\\s-1 \end{matrix} \Big) \times \Large \{ \normalsize \begin{matrix} k-1\\n-s \end{matrix} \Large \rbrace \]

但是要转化可能非常麻烦，还有另一种思路：
对于每个球，自己和同一个盒子里的其他球对它有贡献。

\[ans = \sum w_i \times (\{_k^n \} + (n-1)\{_k^{n-1} \} ) \]

呱算了能看就行

第二类斯特林数怎么算？
相当于 n个有区别的球放进m个无区别的盒子的方案数。可以考虑容斥：

\[\{_n^m\} = \frac{1}{m!} \sum_{k=0}^{m} (-1)^k \cdot (_k^m) \cdot (m-k)^n \]

相当于你钦定有至少k个是空的的方案数

另外，关于递推求逆元的证明：

\[\lfloor \frac{m}{i} \rfloor \cdot i + m \% i = m \equiv 0 \pmod m \]

然后除以\(i \times m \% i\)就得到递推式：inv[i] = (m-m/i) * inv[m%i]

great explaination

CF1370F2 交互 104 26 73 6 1483

先思考特殊情况，比如链和菊花

CF1458C 矩阵？ 105 26 74 6 1498

\(T\) 组测试数据，每次给一个 \(n\times n\) 的矩阵，每行每列都是个 \(1\to n\) 的排列。有 \(m\) 次操作，如果是 UDLR 就是要把整个矩阵每行/每列往一个方向循环移动一格。如果是 IC，就是把矩阵每行/每列变成原来的逆排列。求最后的矩阵。

涉及这种逆排列，考虑其本质，就算相当于其位置与值形成二元组\((i,a_i)\)中，\(i\)与\(a_i\)交换了，变成\((a_i,i)\)。对于本题，相当于三元组\((i,j,a_{(i,j)})\)的一些变换

CF1254D 树 106 26 75 6 1513

这种修改时需要把每个儿子都更新一遍的题，有两种思路：

1. 从儿子找父亲
2. 根号做法。度数大于\(\sqrt n\) 的节点个数不超过\(O(\sqrt n)\)个，所以可以对于度数小的节点暴力更新，对于度数大的节点打标记。

CF1149C 线段树 括号序列 107 26 76 6 1528

给你一棵树的括号序列，有\(m\)次询问，每次询问表示交换两个括号，输出交换两个括号后的直径（保证每次操作后都为一棵树）

这个括号序列就相当于树的欧拉序。
直径，即最长的一条链。
链在欧拉序列上表示为一段区间，其中匹配的括号可以删除。
剩下的括号形如) ) ) ( ( (
这个问题转化为：给(设权值为1，给）设权值为-1，找到两个相邻的区间，使得后面的权值和减去前面的权值和最大。
这个用线段树维护。注意处理pushdown。

CF201D 状压dp 108 26 77 6 1543

对于一个值域为n的序列，我们定义其差异大小。在这个序列中取出一个子序列，使得它是一个\(1\)到\(n\)的排列，且逆序对数量最小。这个最小值定义为这个序列的差异大小

给定\(m\)个长度为\(len\)、值域为\(n\)的序列，问这\(m\)个序列中，差异大小最小的是哪个。

\(n \le 15 , m \le 10 , len \le 5e5\)，时限5秒

考虑现在未知的东西有三个：数字集合、考虑到的位置、逆序对个数。

注意到逆序对个数少于\(n^2\)个，很小。所以把这个放进状态里。

设置状态\(dp[S][i]\)表示数字集合为S，逆序对数量为i，最早结束位置是哪里。

这个转移是\(O(n)\)的：枚举子序列中最后一个数字是j，则最后一个数字产生的逆序对已知。只需要维护每个位置之后，每个数字出现的最早位置即可。

CF482C 状压dp 109 26 78 6 1558

CF1209E2 状压dp 110 26 79 6 1573

CF1830D 树上背包 111 26 80 6 1588

对于 \(i\) 的上界为 \(k\) 的树形背包，其时间复杂度是 \(O(nk)\)。

树形背包要写成 \(f[u][i+j] = \max \{ f[u][i]+f[v][j] \}\) 的形式

CF1120D 树形dp 建图 最小生成树 112 26 81 6 1603

CF1009F 长链剖分 113 26 82 6 1618

长链剖分就是，树形dp过程中出现的状态数量只与最长链长度有关时的优化操作。

具体做法是，遍历到每个节点时，\(O(1)\)合并其重儿子信息（用deque无敌方便），对于所有轻儿子，以\(O(fdep[v])\)的复杂度进行dp。

复杂度证明是，对于每条长链，只会在链顶进行复杂度为链长的dp。总复杂度\(O(n)\)

P3354 树形dp 114 26 83 6 1633

树的节点是村庄，边是河流。点有点权，边有边权，费用是到关键祖宗的距离乘以点权。要求选k个关键点，最小化费用。

设计与【到祖宗的距离】有关的状态，以防止【与子树外有关】的问题。

设\(f[u][zu][i]\) 表示在子树u中设i个关键点，最近的祖先是zu的最小费用。复杂度\(O(n^2k)\)
需要特判zu与u重合的情况，或者u是关键点的情况

P6419 树形dp 115 27 84 6 1648

树上有k个关键点。对于树上每个点求出，从这个点出发把每个关键点都遍历一遍的最短路径。

容易的树形dp。更新时：（感觉容易写复杂啊）

void update(int u,int v,int w){
	int op=1;
	if(u==mxh[v]) op=2;
	if(~mx[v][op] && mx[v][op]+w > mx[u][1]){
		mx[u][2] = mx[u][1];
		mx[u][1] = mx[v][op]+w;
		mxh[u] = v;
	}
	else if(~mx[v][op] && mx[v][op]+w > mx[u][2])
		mx[u][2] = mx[v][op]+w;
}

P3565 & P5904 树形dp 长链剖分 117 27 86 6 1663

给定一棵树，在树上选 3 个点，要求两两距离相等，求方案数。

\(n \le 5000\)
\(bonus: n \le 1e5\)

考虑有以下三种形式

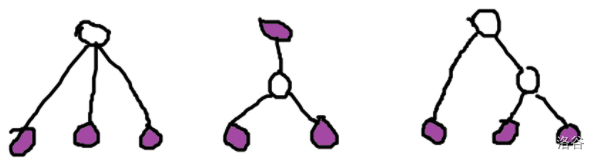
其中1、2是3的特例
所以考虑处理3
设置状态\(f[u][i]\)表示在子树u中到u的距离为i的点的个数
设置状态\(g[u][i]\)表示在子树u中，假设有中心节点p，有点对(x,y)到p的距离同为dis，在子树g外寻找一个节点，使得这个点到p的距离也为dis，且到u的距离为i，点对(x,y)的个数。
可以\(O(n^2)\)转移

可以通过长链剖分优化到\(O(n)\)

CF543D 树形dp 118 27 87 6 1678

简单的dp，但是涉及乘上又除掉+取模，就不能用乘法逆元，要用前后缀和。

CF1446D1 贪心(好题) 119 27 88 6 1693

给定长度为n的序列a，值域为[1,100]，要选出一个区间，使得区间中的众数有两个或以上。问这个区间最长是多长。

结论：整个序列的众数x一定也是这个区间的两个众数之一。

证明：对于任意一个有两个众数的区间，一定可以通过扩展区间端点，使得x成为区间的一个众数。

8.6 模拟赛

由于整场死磕T2，并没有很想好好打这场模拟赛导致的。
发现对于T1这种细节较多的简单题，尤其是搜索，我是擅长的。
立个明天好好打模拟赛的flag。

T2 平衡树 120 27 89 6 1708

区间加，区间翻转，求区间和。\(n \le 10^9 , m \le 2.5e5\)

n 较大，考虑类似离散化，每个点都代表一段数值相等的区间。不能说每个叶子都代表一段区间，因为在合并过程中会移动到非叶子的地方。

T3 dp 121 27 90 6 1723

给出序列a，定义一个子序列的权值为【所有在子序列内的位置的权值和】 × 【不在子序列内的位置的权值和】。问所有最长上升子序列的权值和。

考虑以i结尾的所有上升子序列。设g[i]表示方案数，f1[i]表示所有方案中选了的权值和，f2[i]表示所有方案中没选的权值和，f[i]所有方案所有位置的乘积，即答案。

8.7 模拟赛

这两场模拟赛其实都是，A掉一道题后就没有继续思考的动力了。其实也是A的太慢的缘故。
对拍的太急了。对于大概有把握的题，没必要花太多时间对拍。反而是样例给的非常不足的题，即使是手造几个小数据也非常有用。由于T4没给部分分的样例，我直接没调就交了，以至于队列没pop。

T1 整体二分 二分答案 好题啊 123 27 92 6 1753

给出一个序列，m个询问，每个询问给定两个区间[l1,r1] , [l2,r2]，表示左端点在第一个区间，右端点在第二个区间，问这个序列的中位数最大是多少（偶数个数的话中位数是）

T2 并查集 124 27 93 6 1768

三种操作，插入数值，查询前驱，查询后继。
\(值域 \in [1,1e7],操作 \le 5\times 10^6\)

注意到值域较小。观察复杂度和值域相关的做法。离线，倒序，变成删数。并查集维护前驱后继。

并查集复杂度带\(\alpha\)是为什么呢，感觉证不了。

T3 bitset dp 背包 125 27 94 6 1783

n种物品，装进L的背包，有个数c和体积v两个限制，给定一个可行的选择种类集合，求所有可以凑出的体积
\(n \le 2 \times 10^3\)

我们不知道的东西有：
当前枚举到哪了，已经用了多少种物品，它们的体积之和是多少
显然如果都放进状态是不行的，转移也爆了。
考虑我们的dp数组是只有0/1的，因此考虑bitset优化。
把【可行的物品种类】压位。
设\(f[i][j][k]\)表示体积和位j，用k种物品，是否可行。（i可以压掉）
对于暴力的转移，\(f[i][j] |= f[i-1][j-p*v[i]]<<1\)
按模v[i]分组，就是一段连续的长位c[i]的区间对转移造成影响。
所以隔c[i]个分一段，用前后缀和预处理。

T4 贪心 合并树的经典题 122 27 91 6 1738

给定一棵树

每个点要选了父亲才可以选

选择每个点要花费一些心情\(a_i\)，然后再得到一些心情\(b_i\)

问初始心情至少是多少，才存在一种选上所有点的方案，使得在任意时刻心情都非负。

对于序列来讲，是排序。
贪心题最好别猜。还是用什么\(exchange\)定理来计算。

对于树来讲，就是合并子树。子树的权值合并后推给父亲，可以用并查集维护连通块。

对于优先队列的使用：不用再反着定义运算符了。nd也可以greater啊。。

8.8

优化建图：

• 前缀--链
• 区间--线段树
• 等距离的点--长链剖分
  总的来说就是建虚拟节点

8.9

T1 位运算 126 27 95 6 1798

P5337 树链剖分 127 27 96 6 1813

• 删点--倒序加点
• 两个儿子大小相同才可能改变。这相当于最多只有log个改变。最多只有log个满足两个儿子大小相等，从根开始到这个叶子，每次子树大小至少减小一半，这也不过log个。

P4126 网络流 128 27 97 6 1828

P1377 笛卡尔树 129 28 97 6 1835

arc115E dp 单调栈 130 29 97 6 1842

给定序列a，要求构造序列x，使得对于所有\(x_i\)，\(x_i \le a_i\) 且 \(x_i \neq x_{i-1}\)。问构造x的方案数。

设 \(f[i]\) 表示前i个数的答案。则有\(f[i] = \sum_{j=0}^i f[i-j-1] \times min \{ a_k \} \times (-1)^j\)

单调栈优化。

CF1580B dp 笛卡尔树 131 29 98 6 1857

笛卡尔树和最大值分治脱不开关系。可以用笛卡尔树的思想解决很多最大值分治的问题。

设 \(f[i][j][k]\) 表示大小为i的树，共有k个节点深度为j的方案数。

转移是 \(O(n^5)\) 的，看起来过不了，但是由于 循环的常数非常小，可以通过如果转移是0就跳过的方式。

CF2002 bnds三巨头出的题！真是太牛了！全是好题！

prob D 132 29 99 6 1872

给定大小为n的一棵树，一个1到n的排列，给定m组询问，每组询问之前会交换排列的两个位置。询问内容为，这个排列是否是这棵树的一个dfn序。

考虑dfn序这个东西。
它满足什么性质。

两个理解角度。

这道题如果按第二种做会很容易。

如果按第一种做也可以。把限制条件放在每一个节点上，表现为，按照儿子的dfn序排序，其子树区间恰好连续，且最小的那个恰好比u的dfn序大1。
记录每个点有多少限制不被满足，以及有多少个点满足了所有限制。

修改时，操作类似于莫队。我们总结为：全局问题，单个修改
这种情况下，一般按照这样的操作顺序：

1. 把要修改的部分原先对最终答案的贡献删去
2. 删去原先的东西。注意删除顺序，尤其是每个东西只能删一遍。
3. 更新值
4. 2的逆操作。最好完全反过来
5. 1的逆操作。

我们要维护一个有序的且能二分的东西。这个用set！

要维护一个集合，且支持插入删除，用set！

prob E 133 29 100 6 1887

给定n个连续数字段，每段有一个长度\(a_i\)和一个数值\(c_i\)，每次会把所有满足 \(x_i \neq x_{i-1}\) 的 \(x_i\) 删掉，问对于每一个前缀，删多少次可以删空。

这种颜色段很有可能是单调栈

烦人的是，会存在删空一些段后，相同数值的段会合并。

考虑如果有一对段，满足 \(i < j\) 且 \(a_i < a_j\) 那 \(a_i\) 肯定不会和后面的产生合并了。可以直接把它删掉。那么形成一个单调递减的

反之，则j不能和前面的合并了。

前者相当于栈的pop操作，后者相当于栈的push操作。

进行pop时，相当于时间至少已经过去 \(a_i\) 了。之后的合并发生时，两个均已经减过当前时间。这个需要注意。

P3231 二分图 134 29 101 6 1902

三维二分图怎么办，发现保证了abc的乘积，就发现\(2^17 \times 17^2\) 可以接受啊。

CF1009G 二分图 135 29 102 6 1917

给定一个长为 \(n\) 的串，字符集 \(\texttt a\) 到 \(\texttt f\)。你可以重排这个串，满足指定 \(m\) 个位置上只能放特定的字符，\(m\) 个位置以及字符集会给出，求字典序最小的串。

字典序最小的题，用贪心+可行性判断来解决。
如何可行性判断？容易联想到网络流。从这6种字符种字符流入，从特定字符流出。但是复杂度显然炸了。这种一般要二分图了。相当于判断二分图是否有完美匹配。这就有hall定理了。
考虑字符种类极少。如果暴力做要把每种字符拆成它出现的次数那么多个一样的点。但是由于这些点没有区别，可以一起处理。

ARC076F 二分图 区间问题 136 29 103 6 1932

数轴上1到m这m个位置上有椅子，有n个人，他们坐椅子有要求，要坐在\(l_i\)及以下或\(r_i\)及以上的位置。问至少增加多少个椅子使得所有人都有位置坐

匹配问题，容易联想到二分图。想到hall定理。对应位置是一段区间。我们要找的就是 \(\max \{ 人数 - 对应区间并 \}\)

为什么要给前后一段区间呢。所以改成l到r之间。\(m - \max \{ 人数 + 对应区间交 \}\)。这样你成功把区间并转化为区间交。这个是可做的

考虑类似扫描线的思想，在每个点维护，以这个点为右端点的最大值。移动左端点来更新答案。建立线段树维护区间信息。

CF360E 最短路 137 29 103 7 1962

P8860 最小生成树 138 29 104 7 1977

8.15 模拟赛

T1 贪心 双指针 139 29 105 7 1992

T2 并查集 区间问题 140 29 106 7 2007

给定n个数，m次操作，每次操作给出数值t，要求所有大于等于t的数都减t，问最后这n个数被分别减了多少次。

\(值域,n,m \le 10^6\)

对于这个值域区间，每次操作相当于是一个缩小区间范围的操作。当t比较小时，可以考虑移动左端点，改变0的位置。操作次数可以用并查集维护。

T4 线性基 树链剖分 141 29 107 7 2022

给定一棵树，每次问，如果删去一条链，剩下的点你来选择选或不选，有多少种异或和为k的方案。

树链剖分后，这条链将整棵树分为了log个区间（dfn序）。进行线性基的合并

8.18

CF1336E1 线性基 状压dp 折半搜索 142 29 108 7 2037

你有一个长度为\(n(n\le200000)\)的序列，每个数的权值小于\(2^m(m\le35)\)

定义一个子序列的权值为子序列所有数的异或和的二进制表示中\(1\)的个数

对于所有\(i\in[0,m]\)，输出所有\(2^n\)个子序列中权值为\(i\)的子序列的个数\(\mod 998244353\)的值

一个dp思路：设\(f[i][j][S]\) 表示考虑到线性基的前i大的位，这前i位有j个1，比i位小的1的集合为S，方案数是多少

暴力转移复杂度\(\Theta(m^2 2^m)\)，但是考虑有值的状态。发现对于i比较大的一些状态，是很空的。设mid=m/2，对于大于等于mid的位暴力枚举所有集合；对于小于mid的位dp转移。

P4151 线性基 143 29 109 7 2052

考虑一个边权为非负整数的无向连通图，节点编号为 \(1\) 到 \(N\)，试求出一条从 \(1\) 号节点到 \(N\) 号节点的路径，使得路径上经过的边的权值的 XOR 和最大。（路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数）

考虑最后的路径可以是什么样。首先肯定有一条1到n的简单路径。其他有一些环。把环放进线性基，随便搞一条路径找异或最大值就行。因为对于其他1到n的路径，一定与当前路径构成环。

如何把所有环放进线性基？考虑tarjan。把所有返祖边构成的环放进去就行。为什么是对的，因为一个经过两条以上返祖边的环肯定可以右这些环异或出来。

CF1220F 笛卡尔树 循环移位 144 29 110 7 2067

给定一个排列，问最少进行多少次循环移位，能使得这个排列对应的笛卡尔树深度最小。

首先1对应树的根不变。其他一半是左子树，一半是右子树，分别计算就行

P4755 最大值分治 145 29 111 7 2082

最大值分治用笛卡尔树很好写啊

ARC104F 区间dp 146 29 112 7 2097

8.19

P4926 差分约束 147 29 113 7 2112

【所有取值方案都能使得A】= !【存在一种方案使得没有A】
对于数字过大的乘法且只需要比较大小，取log值
卡精度：1e-7足够了，其他不是精度问题。
差分约束0点初值：本来设成啥都可以，但如果有固定权值，则设无穷大
由于差分约束共有 n+1 个点，spfa时sum要到达n+2才是负环

P5787 可撤销并查集 线段树分治 148 30 113 7 2119

可撤销并查集别路径压缩了啊喂

8.23 模拟赛

构造

CF1685C 括号匹配

给定一个括号序列，问最少进行多少次区间reverse操作使得括号匹配合法
\(n \le 10^5\)

括号匹配问题，可能大概有三种思路：

• (代表向右走，)代表向上走，匹配就是卡特兰数
• 栈，栈和括号匹配可以相互转化
• (代表1，)代表-1，匹配就是前缀和时刻大于等于0

此题用最后一种。
考虑最终答案不会超过2。因为在这个前缀和最大处把前后两半revers一定是合法的。
然后再特判答案是否可能是0/1

arc180B

给定一个1到n的排列，每次操作可以选择一对距离大于等于k的逆序对并交换他们，问最大操作次数及方案
\(n \le 500\)

原排列的满足条件的逆序对所在的位置组成的二元组都可以成为最终答案。

这种构造要无后效性的，也就是前面的操作不要影响后面的操作。可以每次取最大值，把它与和它配对的位置从大到小依次交换。

arc145D

构造一个长度为n的序列，使得其中没有长度为3的等差数列，且所有元素和为m
\(n \le 1e4 , m \le 1e10\)

先不考虑和为m的限制，考虑怎样一个序列是合法的。发现在三进制下只有0和1的数形成的集合是合法的。为什么呢，因为这样的数乘2后肯定没有1的，但是两个不相等的这样的数加起来一定有1。

可以留最后一位不构造，最后如果有余数，就随便找一些数加1

arc119D

给定一个n * m的矩阵，其中有一些格子是红色的，每次操作可以选择一个红色的格子，并把它所在的一行或者一列染成白色，问最多把多少格子染成白色。

等价于，对应二分图上，选出一些边，这些边指向它的一个端点，这个端点不能再有其他边指向它。那其实形成一个外向树森林。

每棵树最后都要留下一个点。这个点怎么选？我们要最小化没有染色的点，这相当于要让剩下的行和列尽量不平均。

cf521E tarjan

给定一张无向图，问是否存在两个点之间有三条不相交的路径

第一眼竟然是圆方树，是不是真没救了！

其实是tarjan，要求两条祖孙链对应的树边有交集，这个交集的上下两个端点即为起点和终点。

qoj7686 哈希 欧拉回路

给你n个长为m的字符串\(A_{1,2,3...},B_{1,2,3...}\)，你需要分别把A,B拼成一个大字符串，你
需要使拼成的两个字符串循环同构。你需要构造方案或者报告无解。
\(nm\le 10^6\)

枚举断点，前后两部分分别哈希然后建点，形成一条前面这个串指向后面这个串的边。每个字符串对应一条边。就是要找一条欧拉回路

CF1991G

CF566E

给你到每个点距离小于等于2的所有点的集合，但你不知道这是哪个点的集合。要求构造一棵满足条件的树。

\(n \le 1000\)

如果给定的集合距离小于等于1，那两个点的交集之间就有一条边。
但是距离小于等于2，那当交集为2时，说明这两个点在树上距离为3，路径上的两个点之间有一条边。但是叶子没有连上，需要特判。

CF1705F

注意到要求的询问次数差不多是\(\frac{2}{3}n\)，考虑一个长为3的子串通过两次询问如何得到答案。可以先询问1到n满足一些特性的答案，然后再改变这三个的答案进行对比得出结果。

树状数组与st表

2024.9.1

CF1140F 线段树分治

定义一个点集合 \(S=\{(x_i,y_i)\}(1\leq i\leq n)\) 的拓展操作为将符合以下条件的 \((x_0,y_0)\) 加入 \(S\)：

• 存在 \(a,b\)，使得 \((a,b),(a,y_0),(x_0,b)\in S\)。

不断执行以上操作直到不能操作，此时得到的集合即为拓展集合。现在给定 \(q\) 个操作，每次加入或删除一个点，重复点即为删除，你需要输出每个操作之后的拓展集合大小（不用真的拓展，只求大小）。

这个东西答案为二分图所有连通块左部点个数乘右部点个数。

所以就离线线段树分治。

P5227 线段树分治

给定一个无向连通图和若干个小集合(这个小集合最大大小为c)，每个小集合包含一些边，对于每个集合，你需要确定将集合中的边删掉后改图是否保持联通。集合间的询问相互独立

\(n,m,q \le 10^5\) , \(c \le 4\)

删边太麻烦了，考虑改成加边。c很小，因此所有边被删掉的次数和也比较小。所以这些边存在的时刻为一些区间，区间总数不超过\(O(qc)\)，所以可以线段树分治解决

P4585 01trie 线段树分治 树套树(?)

一排n个商店，初始时第\(i\)个商店有一种价值为\(val_i\)的商品，每次操作为以下两种：

• 开启新的一天，并在第\(x\)个商店进购一种价值为\(c\)的商品
• 在l到r这段区间里的商店里买东西，要求进购时间在d天以内或一开始就有，问买到的价格与x异或和的最大值
  输入的所有数小于1e5

sol1

最大异或和在01trie上考虑。但是如何判断能不能继续往下走？考虑能往下走的充要条件是，当前在l到r的的区间内有至少一种商品的进购时间晚于要求时间。这个线段树好维护。所以就在trie上每个点建立动态开点线段树就行

sol2

询问相当于问在一段时间的区间内能够进购到的价值。对于时间的区间，这个用线段树分治了。考虑把所有询问挂在节点上，则这个子树内的所有时刻均合法。每到一个节点，就暴力重构这个区间内的可持久化trie。复杂度为什么是对的，因为每个更新只会在trie上加log次。

这两种解决方案，就差不多，一个是先解决空间限制再解决时间限制，一个是先解决时间限制再解决空间限制。还挺有意思的啊

CF576E

给定一张 \(n\) 个点 \(m\) 条边的无向图。

一共有 \(k\) 种颜色，一开始，每条边都没有颜色。

定义合法状态为仅保留染成 \(k\) 种颜色中的任何一种颜色的边，图都是一张二分图。

有 \(q\) 次操作，第 \(i\) 次操作将第 \(e_i\) 条边的颜色染成 \(c_i\)。

但并不是每次操作都会被执行，只有当执行后仍然合法，才会执行本次操作。

你需要判断每次操作是否会被执行。

\(n,m,q \le 5 \times 10^5\)，\(k \le 50\)。

P5283 异或粽子 前k大 字典树

给定长度为n的序列a，其中一个子串的权值是其中数的异或和，问异或和第k大的子串

对序列做前缀和后，只与前后端点权值有关，把所有数存到trie树上，用超级钢琴那个思路用优先队列可以搞，每次更新就是找到第一个可以改的不优的祖先，然后换一个儿子往下按最优方案走。

但是有一个问题就是一个叶子节点代表很多位置怎么办。如果单纯记录cnt，无法判断与当前位置的大小关系

考虑令k=k*2，这样就不用考虑先后关系了。

P9576 z函数 字符串 二分哈希

给定字符串s和模式串t，在s中选两个子区间，问有多少种选法，使得这两个子区间拼起来恰为t

设 \(pre_i\) 表示以i为第一个子串的起点，最多匹配多少位，\(suf_i\) 表示以i为第二个子串的终点，最多匹配多少位。求这个东西可以z函数，也可以二分哈希。然后对于每个i计算其作为第一个子串的起点的答案，按i从大到小看，每个suf相当于一个区间加的操作（对于越靠前的位置加的越多，就相当于从m-suf这个位置开始到1，每个位置都加1）。就是简单的区间修改区间查询操作了