机器学习笔记（一）——代价函数

在线性回归中我们有一个像这样的训练集，m代表了训练样本的数量，比如 m=47。而我们的假设函数，也就是用来进行预测的函数，是这样的线性函数形式：\(h_{\theta}(x)=\theta_0+\theta_1x\)。
接下来我们会引入一些术语我们现在要做的便是为我们的模型选择合适的参数（parameters）\(θ_0\) 和 \(θ_1\)，在房价问题这个例子中便是直线的斜率和在y轴上的截距。
我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

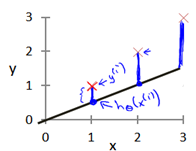
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数\(J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_{theta}(x^{(i)})-y^{(i)})^2\)最小。
我们绘制一个等高线图，三个坐标分别为\(θ_0\)和\(θ_1\)和\(J(θ_0,θ_1)\)：

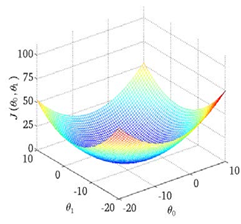
则可以看出在三维空间中存在一个使得\(J(θ_0,θ_1)\)最小的点。
代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。