arc板刷

RT

记录一下板刷的过程a.a

arc050

a

题意

给你两个字符，问它们不管大小写后是不是同一个字母

sol

点击输入文本。
submission

b

题意

给你 \(r, b, x, y\)，问最大的 \(k\)，使得存在 \(m, n \in \N^+, m+n=k\) 且满足 \(mx + n \leq r, ny + m \leq b\)。

sol

考虑分析这个要求的式子，可以直接去移项得到 \(m,n\) 各自的关于给定参数的上界，即 \(m \leq \lfloor\frac{r-k}{x-1}\rfloor, n \leq \lfloor\frac{b-k}{y-1}\rfloor\)。

显然 \(k\) 越大，对于 \(m, n\) 的限制就越严，因此我们直接对于大于等于 mid，是否存在满足条件的 \(k\) 二分答案就好了。

submission

c

题意

给你两个数 \(a, b\)，其中 \(a\) 由 \(A\) 个 \(1\) 组成，\(b\) 由 \(B\) 个 \(1\) 组成。

问你 \(\operatorname{lcm}(a,b) \bmod m\) 的值。

sol

考虑 \(\operatorname{lcm}(a,b)\) 的本质，熟知 \(\operatorname{lcm}(a,b)=\frac{ab}{(a,b)}\)，于是我们拆开原式子。

不妨设 \(a_x\) 表示由连续 \(x\) 个 \(1\) 组成的数字。我们有以下结论：\(\forall x, y \in \N^+, x > y, 有 \gcd(a_x,a_y)=a_{\gcd(x,y)}\)。
证明是容易的，考虑 \(\gcd(a_x,a_y)=\gcd(a_x-a_y,a_y)=\gcd(10^{x-y}a_{x-y},a_y)\)，又显然有 \(\forall x,2\nmid a_x, 5\nmid a_x\)，所以 \(\gcd(10^{x-y}a_{x-y},a_y)=\gcd(a_{x-y},a_y)\)，所以就化归到了下标上的 \(\gcd\)。

于是我们只需要求 \(a_A \bmod m\) 和 \(\frac{a_B}{a_{\gcd(A,B)}} \bmod m\) 的值，注意到前后者都有一个固定的循环节，所以可以用矩阵加速递推来求出其值，实现是容易的。

submission

arc058

a

题意

买家想买一个价格为N的物品，但他又讨厌k个数字，分别为D_1，D_2，……，D_K。问他最少出多少钱，才能在保证买下这个物品的同时使自己出的钱不包括自己讨厌的数字。

sol

枚举即可
submission

b

问题陈述

我们有一个行数为 \(H\) 列数为 \(W\) 的大正方形网格。伊罗哈现在站在左上角的单元格中。她将重复向右或向下移动到相邻的单元格，直到到达右下方的单元格。

但是，她无法进入最下面的 \(A\) 行和最左边的 \(B\) 列相交的单元格。进入其他单元格没有限制。

求她可以通过几种方式到达右下角的单元格。

由于这个数字可能非常大，请打印出这个数字的模数 \(10^9+7\) 。

sol

有经典的方格图 \((x,y)\) 到 \((a,b),x\leq a, y \leq b\)，只能向右上角走的方案数：\(\binom{a-x+b-y}{a-x}\)。

证明考虑到达终点总共 \(a-x+b-y\) 步，有 \(a-x\) 步向右，\(b-y\) 步向上。好了。
记 \(g(x,y,a,b)\) 为 \(\binom{a-x+b-y}{a-x}\)。
然后只需要将向右上角走改为向右下角走，并求 \(\sum g(1,1,b,i)\times g(b+1,i,m,n)\)
就做完了。

比如说这样：

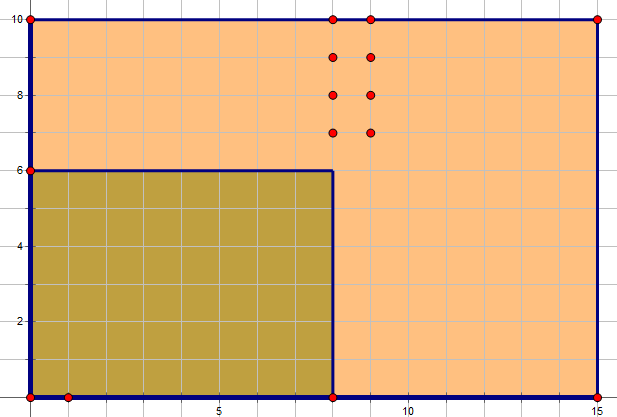
红点就是可以转移的地方。
submission

arc059

a

唐

问题陈述

埃维有 \(N\) 个整数 \(a_1,a_2,..,a_N\) 。他的目标是通过变换其中的一些整数，使 \(N\) 等于相同整数。

每个整数他最多可以变换一次。将一个整数 \(x\) 转化为另一个整数 \(y\) 需要花费 \((x-y)^2\) 美元。即使是 \(a_i=a_j (i≠j)\) ，他也必须为转换每个整数分别支付费用（见示例 2）。

求实现目标所需的最小总成本。

sol

根据 \(\bar{a} = \frac{\sum a_i}{n}\)，向下取整向上取整答案取个 min。
submission

b

有点小牛，但很唐。

问题陈述

给定一个字符串 \(t\) ，当且仅当 \(t\) 的长度至少为 \(2\) ，且 \(t\) 中一半以上的字母相同时，我们才将其称为 _不平衡字符串。例如，"voodoo "和 "melee "都是不平衡的，而 "noon "和 "a "都不是。

给你一个由小写字母组成的字符串 \(s\) 。请判断 \(s\) 中是否存在不平衡的（连续）子串。如果答案是肯定的，请指出在 \(s\) 中出现该子串的位置。

sol

容易发现，只要有一个串形如 aa，aba 即满足情况。枚举即可。

submission

c

dp + 组合数

submission

d

唐诗DP，为什么有紫？

问题陈述

Sig 制作了自己的键盘。这个键盘设计得非常简单，上面只有 \(3\) 个键："0 "键、"1 "键和退格键。

首先，他在这个键盘上使用一个纯文本编辑器。该编辑器始终显示一个字符串（可能为空）。编辑器刚启动时，这个字符串是空的。当按下键盘上的每个键时，字符串会发生以下变化：

• 0 "键：在字符串右侧插入字母 "0"。
• 1 "键：在字符串右侧插入字母 "1"。
• 退格键：如果字符串为空，则不会发生任何操作。否则，字符串最右边的字母将被删除。

Sig 启动了编辑器，总共按了 \(N\) 次这些键。结果，编辑器显示了一个字符串 \(s\) 。求这种按键方式的次数，取模 \(10^9 + 7\) 。

sol

显然有：\(0,1\) 键等价。
所以答案只与输入字符串的长度有关。
容易列出 \(dp_{i,j}\) 表示现在输入了 \(i\) 次，完成了 \(j\) 个字符所用的方案数。
转移方程显然，\(dp_{i,j}=2\times dp_{i-1,j+1}+dp_{i-1,j-1}\) 分别从这一次按退格（所以上一次输入的数可能为 \(0,1\) 两种），和输入正确的数来。

实现简单。
submission