实验四：二叉树

这个作业属于哪个课程	https://edu.cnblogs.com/campus/qdu/DS2020
这个作业要求在哪里	https://edu.cnblogs.com/campus/qdu/DS2020
这个作业的目标	<1、掌握二叉树的基本特性；2、掌握二叉树的先序、中序、后序的递归遍历算法；3、理解二叉树的先序、中序、后序的非递归遍历算法；4、通过求二叉树的深度、叶子结点数和层序遍历等算法，理解二叉树的基本特性>
学号	2018204133

一、实验目的
1、掌握二叉树的基本特性
2、掌握二叉树的先序、中序、后序的递归遍历算法
3、理解二叉树的先序、中序、后序的非递归遍历算法
4、通过求二叉树的深度、叶子结点数和层序遍历等算法，理解二叉树的基本特性

二、实验预习
说明以下概念
1、二叉树：
二叉树是树形结构的一个重要类型。二叉树是n个结点的有限集，它或者是空集（n=0）,或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。
2、递归遍历：
二叉树的定义是递归的，一棵非空的二叉树是由根结点、左子树、右子树这三个基本部分组成的，因此，遍历一棵非空二叉树的问题可分解为三个子问题：访问根节点；遍历左子树；遍历右子树。
3、非递归遍历：
树的遍历若采用非递归的方法，就要采用栈去模拟实现。
4、层序遍历：
除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
三、实验内容和要求
1、阅读并运行下面程序，根据输入写出运行结果，并画出二叉树的形态。

#include<stdio.h>
#include<malloc.h>
#include<iostream>
#include<conio.h>
#define MAX 20
typedef struct BTNode{       /*节点结构声明*/
	char data ;               /*节点数据*/
	struct BTNode *lchild;
	struct BTNode *rchild ;  /*指针*/
}*BiTree;

void createBiTree(BiTree *t){ /* 先序遍历创建二叉树*/
	char s;
	BiTree q;
	printf("\nplease input data:(exit for #)");
	s=getche();
	if(s=='#'){*t=NULL; return;}
	q=(BiTree)malloc(sizeof(struct BTNode));
	if(q==NULL){printf("Memory alloc failure!"); exit(0);}
	q->data=s;
	*t=q;
	createBiTree(&q->lchild); /*递归建立左子树*/
	createBiTree(&q->rchild); /*递归建立右子树*/
}

void PreOrder(BiTree p){  /* 先序遍历二叉树*/
    if ( p!= NULL ) {
       	printf("%c", p->data);
       	PreOrder( p->lchild ) ;
       	PreOrder( p->rchild) ;
    }
}
void InOrder(BiTree p){  /* 中序遍历二叉树*/
    if( p!= NULL ) {
 	 InOrder( p->lchild ) ;
   	 printf("%c", p->data);
   	 InOrder( p->rchild) ;
    }
}
void PostOrder(BiTree p){  /* 后序遍历二叉树*/
   if ( p!= NULL ) {
    	PostOrder( p->lchild ) ;
       	PostOrder( p->rchild) ;
       	printf("%c", p->data);
    }
}
void Preorder_n(BiTree p){ /*先序遍历的非递归算法*/
    BiTree stack[MAX],q;
    int top=0,i;
    for(i=0;i<MAX;i++) stack[i]=NULL;/*初始化栈*/
    q=p;
    while(q!=NULL){
        printf("%c",q->data);
        if(q->rchild!=NULL) stack[top++]=q->rchild;
        if(q->lchild!=NULL) q=q->lchild;
        else
            if(top>0) q=stack[--top];
            else q=NULL;
    }
}
void release(BiTree t){ /*释放二叉树空间*/
  	if(t!=NULL){
    	release(t->lchild);
    	release(t->rchild);
    	free(t);
  	}
}
int main(){
    BiTree t=NULL;
    createBiTree(&t);
    printf("\n\nPreOrder the tree is:");
    PreOrder(t);
    printf("\n\nInOrder the tree is:");
    InOrder(t);
    printf("\n\nPostOrder the tree is:");
    PostOrder(t);
    printf("\n\n先序遍历序列（非递归）:");
    Preorder_n(t);
    release(t);
    return 0;
}

运行程序
输入：
ABC##DE#G##F###
运行结果：

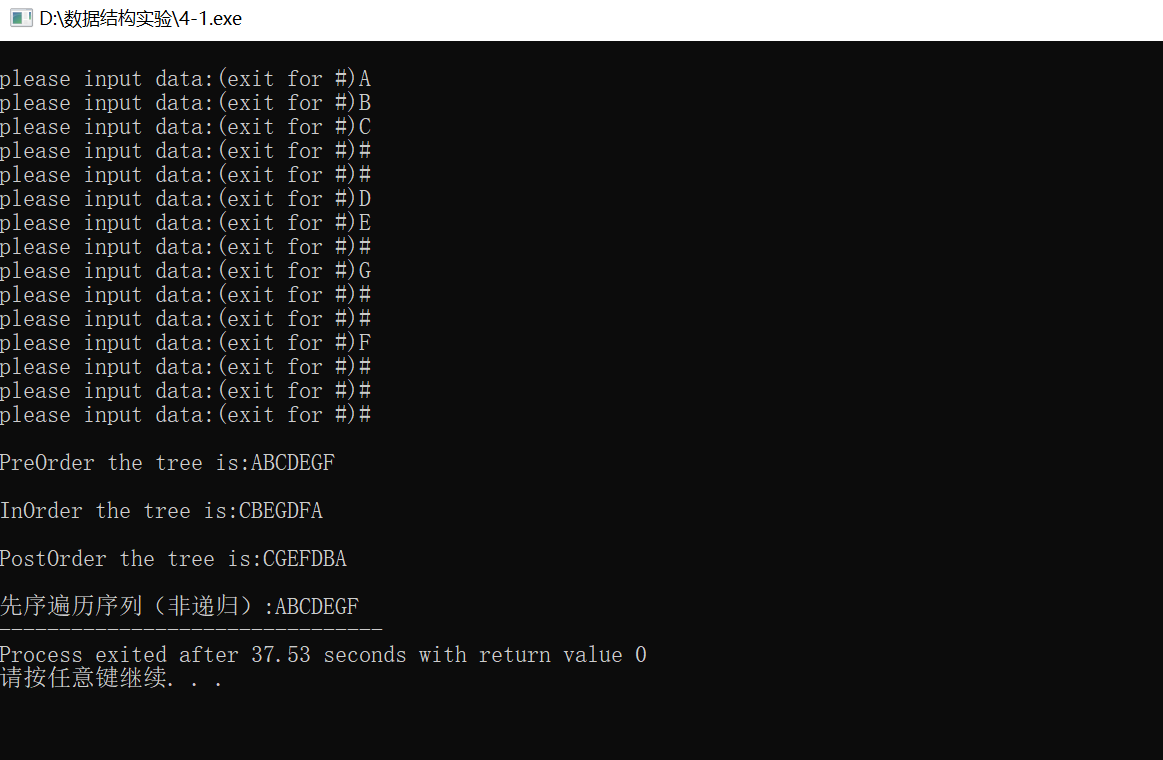
二叉树形态：

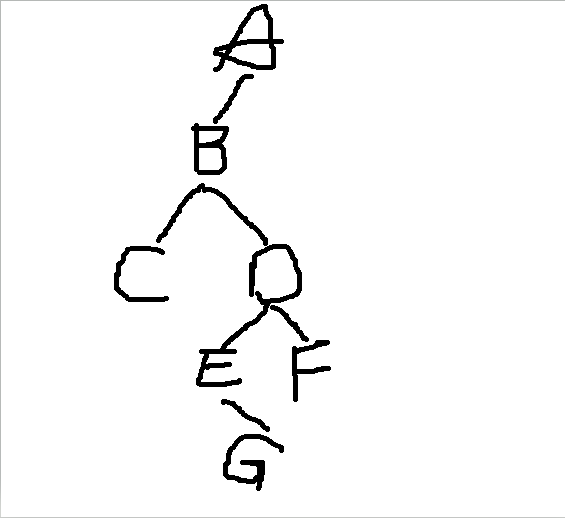
2、在上题中补充求二叉树中求结点总数算法（提示：可在某种遍历过程中统计遍历的结点数），并在主函数中补充相应的调用验证正确性。
算法代码：

#include<stdio.h>
#include<malloc.h>
#include<iostream>
#include<conio.h>
#define MAX 20
typedef struct BTNode{       /*节点结构声明*/
	char data ;               /*节点数据*/
	struct BTNode *lchild;
	struct BTNode *rchild ;  /*指针*/
}*BiTree;

void createBiTree(BiTree *t){ /* 先序遍历创建二叉树*/
	char s;
	BiTree q;
	printf("\nplease input data:(exit for #)");
	s=getche();
	if(s=='#'){*t=NULL; return;}
	q=(BiTree)malloc(sizeof(struct BTNode));
	if(q==NULL){printf("Memory alloc failure!"); exit(0);}
	q->data=s;
	*t=q;
	createBiTree(&q->lchild); /*递归建立左子树*/
	createBiTree(&q->rchild); /*递归建立右子树*/
}

void PreOrder(BiTree p){  /* 先序遍历二叉树*/
    if ( p!= NULL ) {
       	printf("%c", p->data);
       	PreOrder( p->lchild ) ;
       	PreOrder( p->rchild) ;
    }
}
void InOrder(BiTree p){  /* 中序遍历二叉树*/
    if( p!= NULL ) {
 	 InOrder( p->lchild ) ;
   	 printf("%c", p->data);
   	 InOrder( p->rchild) ;
    }
}
void PostOrder(BiTree p){  /* 后序遍历二叉树*/
   if ( p!= NULL ) {
    	PostOrder( p->lchild ) ;
       	PostOrder( p->rchild) ;
       	printf("%c", p->data);
    }
}
void Preorder_n(BiTree p){ /*先序遍历的非递归算法*/
    BiTree stack[MAX],q;
    int top=0,i;
    for(i=0;i<MAX;i++) stack[i]=NULL;/*初始化栈*/
    q=p;
    while(q!=NULL){
        printf("%c",q->data);
        if(q->rchild!=NULL) stack[top++]=q->rchild;
        if(q->lchild!=NULL) q=q->lchild;
        else
            if(top>0) q=stack[--top];
            else q=NULL;
    }
}
void release(BiTree t){ /*释放二叉树空间*/
  	if(t!=NULL){
    	release(t->lchild);
    	release(t->rchild);
    	free(t);
  	}
}
int PreOrder_num(BiTree p) {
	int j=0;
	BiTree stack[MAX],q;
	int top=0,i;
	for(i=0; i<MAX; i++) stack[i]=NULL; /*初始化栈*/
	q=p;
	while(q!=NULL) {
		j++;
		if(q->rchild!=NULL) stack[top++]=q->rchild;
		if(q->lchild!=NULL) q=q->lchild;
		else
			if(top>0) q=stack[--top];
			else q=NULL;
	}
    return j;
}
int main(){
    BiTree t=NULL;
    createBiTree(&t);
    printf("\n\nPreOrder the tree is:");
    PreOrder(t);
    printf("\n\nInOrder the tree is:");
    InOrder(t);
    printf("\n\nPostOrder the tree is:");
    PostOrder(t);
    printf("\n\n先序遍历序列（非递归）:");
    Preorder_n(t);
    printf("\n\n结点总数:");
    printf("%d",PreOrder_num(t));
    release(t);
    return 0;
}

运行结果：

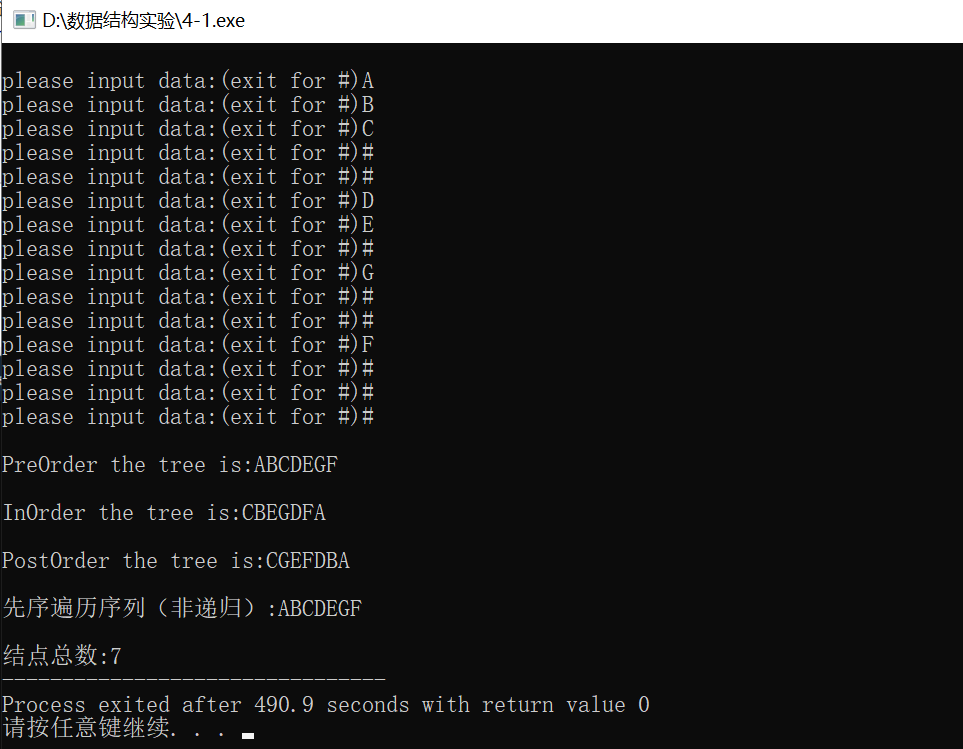
3、在上题中补充求二叉树中求叶子结点总数算法（提示：可在某种遍历过程中统计遍历的叶子结点数），并在主函数中补充相应的调用验证正确性。
算法代码：

int LeafNodes(BiTree p) {
	int num1=0 ,num2=0;
	if(p==NULL)
	return 0;
	else if(p->lchild==NULL&&p->rchild==NULL)
	return 1;
	else{ 
		num1=LeafNodes(p->lchild) ;
		num2=LeafNodes(p->rchild) ;
 		return (num1+num2);
    }
} 
int main(){
    BiTree t=NULL;
    createBiTree(&t);
    printf("\n\nPreOrder the tree is:");
    PreOrder(t);
    printf("\n\nInOrder the tree is:");
    InOrder(t);
    printf("\n\nPostOrder the tree is:");
    PostOrder(t);
    printf("\n\n先序遍历序列（非递归）:");
    Preorder_n(t);
    printf("\n\n结点总数:");
	printf("%d",PreOrder_num(t));
    printf("\n\n叶结点总数："); 
    printf("%d",LeafNodes(t));   
    release(t);
    return 0;
}

运行结果：

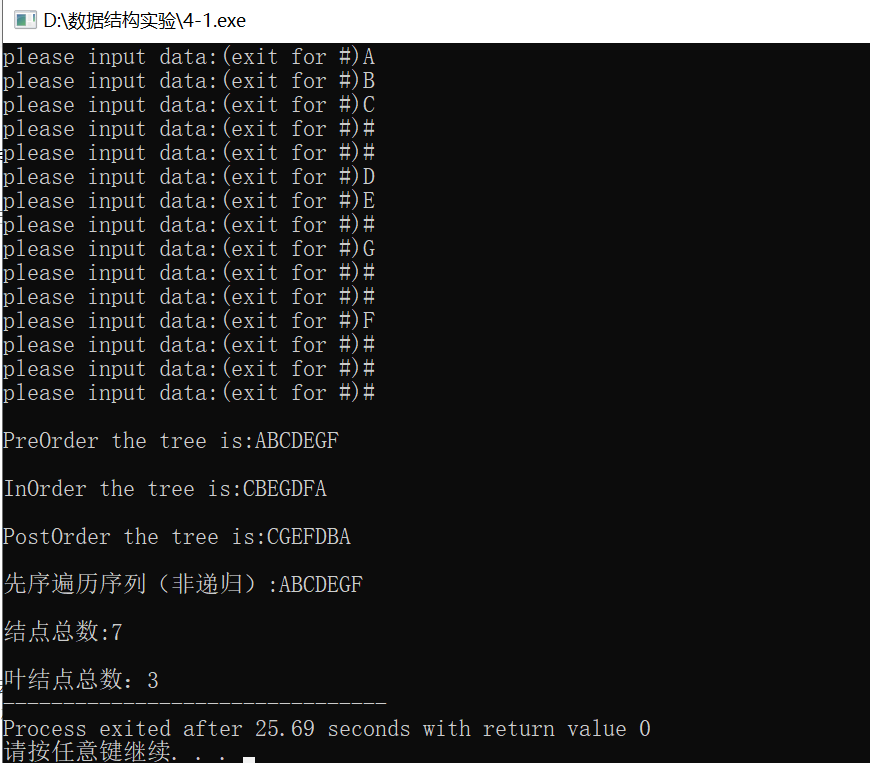
4、在上题中补充求二叉树深度算法，并在主函数中补充相应的调用验证正确性。
算法代码：

int BTNodeDepth(BiTree p) {
	int lchilddep,rchilddep;
	if(p==NULL)
		return 0;
	else {
		lchilddep=BTNodeDepth(p->lchild);
		rchilddep=BTNodeDepth(p->rchild);
		return(lchilddep>rchilddep)?(lchilddep+1):(rchilddep+1);
	}
}
int main(){
    BiTree t=NULL;
    createBiTree(&t);
    printf("\n\nPreOrder the tree is:");
    PreOrder(t);
    printf("\n\nInOrder the tree is:");
    InOrder(t);
    printf("\n\nPostOrder the tree is:");
    PostOrder(t);
    printf("\n\n先序遍历序列（非递归）:");
    Preorder_n(t);
    printf("\n\n结点总数:");
    printf("%d",PreOrder_num(t));
    printf("\n\n树的深度:");
    printf("%d",BTNodeDepth(t));    
    release(t);
    return 0;
}

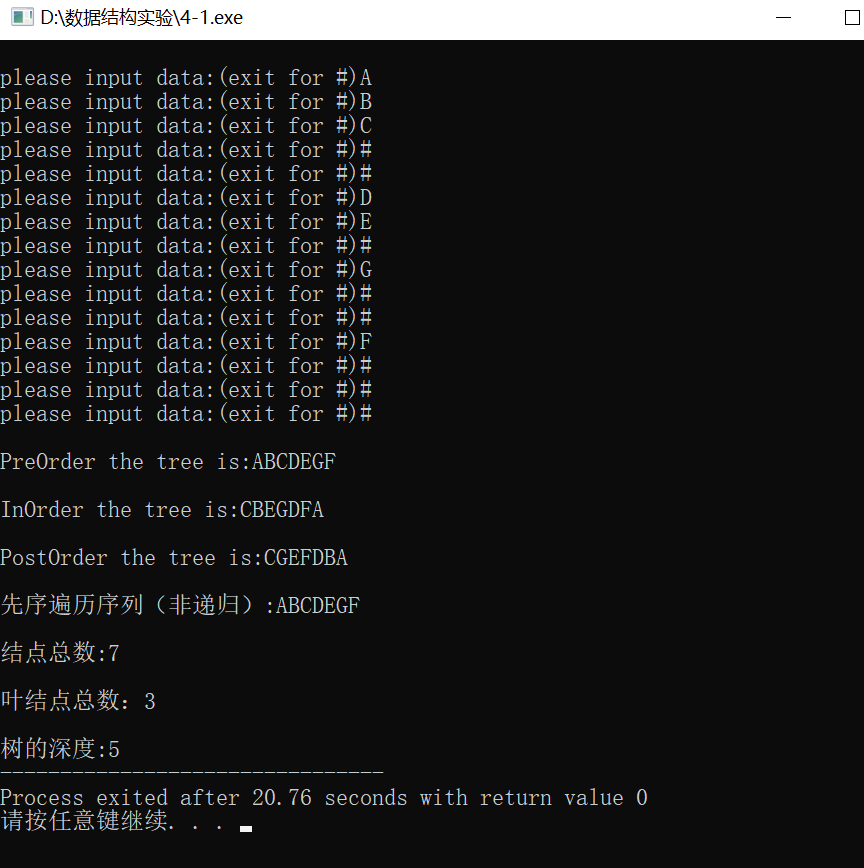
运行结果：

选做实验：（代码可另附纸）
1、补充二叉树层次遍历算法。（提示：利用队列实现）

5、补充二叉树中序、后序非递归算法。

四、实验小结
具体应用代码遍历树并给出求树的结点总数、深度、叶结点总数的代码，具体代码实现仍需加强。

五、评语

posted on 2020-11-04 20:06 TlostGeneration 阅读(1198) 评论(0) 收藏举报