实验二：栈和队列

这个作业属于哪个课程	https://edu.cnblogs.com/campus/qdu/DS2020
这个作业要求在哪里	https://edu.cnblogs.com/campus/qdu/DS2020/homework/11296
这个作业的目标	<1、掌握栈的结构特性及其入栈，出栈操作；2、掌握队列的结构特性及其入队、出队的操作，掌握循环队列的特点及其操作。>
学号	2018204133

一、实验目的
1、掌握栈的结构特性及其入栈，出栈操作；
2、掌握队列的结构特性及其入队、出队的操作，掌握循环队列的特点及其操作。

二、实验预习
说明以下概念
1、顺序栈：
栈是限制仅在表的一端进行插入和删除运算的线性表。栈的顺序存储结构简称为顺序栈，它是运算受限制的顺序表。顺序栈是指利用顺序存储结构实现的栈。采用地址连续的存储空间（数组)依次存储栈中数据元素，由于入栈和出栈运算都是在栈顶进行，而栈底位置是固定不变的，可以将栈底位置设置在数组空间的起始处；栈顶位置是随入栈和出栈操作而变化的，故需用一个整型变量top来记录当前栈顶元素在数组中的位置。
2、链栈：
栈的链式存储结构称为链栈。它是运算受限的单链表，其插入和删除操作仅限制在表头位置上进行。由于只能在链表头部进行操作，故链栈没有必要像单链表那样需附加头结点。栈顶指针就是链表的头指针。
3、循环队列：
为充分利用向量空间，克服"假溢出"现象的方法是：将向量空间想象为一个首尾相接的圆环，并称这种向量为循环向量。存储在其中的队列称为循环队列。
4、链队：
队列的链式存储结构称为链队列，它是限制仅在表头删除表尾插入的单链表。
三、实验内容和要求
1、阅读下面程序，将函数Push和函数Pop补充完整。要求输入元素序列1 2 3 4 5 e，运行结果如下所示。

#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
#define STACK_INT_SIZE 10  /*存储空间初始分配量*/
#define STACKINCREMENT 5  /*存储空间分配增量*/
typedef  int ElemType; /*定义元素的类型*/
typedef struct{
    ElemType *base;
    ElemType *top;
    int stacksize;     /*当前已分配的存储空间*/
}SqStack;

int InitStack(SqStack *S);   /*构造空栈*/
int push(SqStack *S,ElemType e); /*入栈*/
int Pop(SqStack *S,ElemType *e);  /*出栈*/
int CreateStack(SqStack *S);     /*创建栈*/
void PrintStack(SqStack *S);   /*出栈并输出栈中元素*/

int InitStack(SqStack *S){
    S->base=(ElemType *)malloc(STACK_INT_SIZE *sizeof(ElemType));
    if(!S->base) return ERROR;
    S->top=S->base;
    S->stacksize=STACK_INT_SIZE;
    return OK;
}/*InitStack*/

int Push(SqStack *S,ElemType e){
	if(S->top-S->base>=S->stacksize){
	S->base=(ElemType*)realloc(S->base,(S->stacksize+STACKINCREMENT)*sizeof(ElemType));
        if(!S->base) return ERROR;
        S->top=S->base+S->stacksize;
        S->stacksize+=STACKINCREMENT;  
    }
    *S->top++=e;
    return OK;}/*Push*/

int Pop(SqStack *S,ElemType *e){
    if(S->top!=S->base){
		*e=*--S->top;
		return OK;
	}
	else
	return ERROR;}/*Pop*/

int CreateStack(SqStack *S){
    int e;
    if(InitStack(S))
        printf("Init Success!\n");
    else{
        printf("Init Fail!\n");
        return ERROR;
    }
    printf("input data:(Terminated by inputing a character)\n");
    while(scanf("%d",&e))
        Push(S,e);
    return OK;
}/*CreateStack*/

void PrintStack(SqStack *S){
    ElemType e;
    while(Pop(S,&e))
        printf("%3d",e);
}/*Pop_and_Print*/

int main(){
    SqStack ss;
    printf("\n1-createStack\n");
    CreateStack(&ss);
    printf("\n2-Pop&Print\n");
    PrintStack(&ss);
    return 0;
}

算法结果：

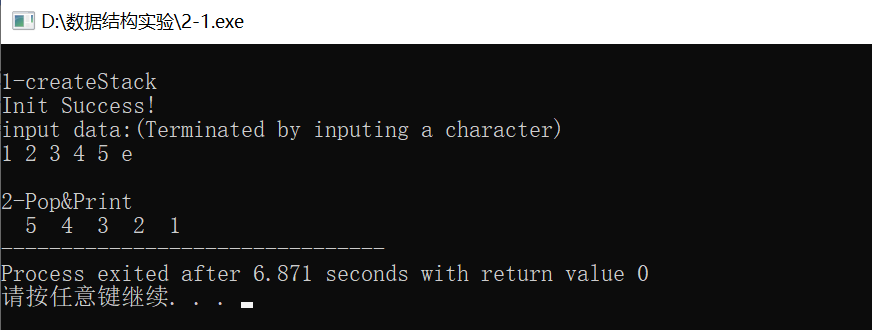
算法分析:输入元素序列1 2 3 4 5，为什么输出序列为5 4 3 2 1？体现了栈的什么特性？
进栈的顺序是1 2 3 4 5，退栈的次序是5 4 3 2 1，体现了栈的修改是按照后进先出的原则进行的。主函数中调用PrintStack(&ss)，在PrintStack(&ss)内，又调用了Pop(SqStack *S,ElemType *e)函数,此函数的功能是栈S的栈顶元素出栈并返回其值。输入元素序列1 2 3 4 5，输出序列为5 4 3 2 1。

2、在第1题的程序中，编写一个十进制转换为二进制的数制转换算法函数（要求利用栈来实现），并验证其正确性。
实现代码

#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
#define STACK_INT_SIZE 10  /*存储空间初始分配量*/
#define STACKINCREMENT 5  /*存储空间分配增量*/
typedef  int ElemType; /*定义元素的类型*/
typedef struct{
    ElemType *base;
    ElemType *top;
    int stacksize;     /*当前已分配的存储空间*/
}SqStack;
int InitStack(SqStack *S);   /*构造空栈*/
int push(SqStack *S,ElemType e); /*入栈*/
int Pop(SqStack *S,ElemType *e);  /*出栈*/
int CreateStack(SqStack *S);     /*创建栈*/
void PrintStack(SqStack *S);   /*出栈并输出栈中元素*/
void conversion(SqStack *S);
int InitStack(SqStack *S){
    S->base=(ElemType *)malloc(STACK_INT_SIZE *sizeof(ElemType));
    if(!S->base) return ERROR;
    S->top=S->base;
    S->stacksize=STACK_INT_SIZE;
    return OK;
}/*InitStack*/

int Push(SqStack *S,ElemType e){
	if(S->top-S->base>=S->stacksize){
		S->base=(ElemType*)realloc(S->base,(S->stacksize+STACKINCREMENT)*sizeof(ElemType));
        if(!S->base) return ERROR;
        S->top=S->base+S->stacksize;
        S->stacksize+=STACKINCREMENT;  
    }
    *S->top++=e;
    return OK;
}/*Push*/

int Pop(SqStack *S,ElemType *e){
    if(S->top!=S->base){
		*e=*--S->top;
		return OK;
	}
	else
	return ERROR;
}/*Pop*/

int CreateStack(SqStack *S){
    int e;
    if(InitStack(S))
        printf("Init Success!\n");
    else{
        printf("Init Fail!\n");
        return ERROR;
    }
    printf("input data:(Terminated by inputing a character)\n");
    while(scanf("%d",&e))
        Push(S,e);
    return OK;
}/*CreateStack*/

void PrintStack(SqStack *S){
    ElemType e;
    while(Pop(S,&e))
        printf("%3d",e);
}/*Pop_and_Print*/

void conversion(SqStack *S) {
	ElemType n,h; 
	int m=0,k=0; 
	InitStack(S); 
	printf("Input a number\n"); 
	scanf("%d",&n);  
	while(n) { 
		m++; 
    	Push(S,n%2); 
    	n=n/2; 
	} 
	while(k<m) {    
		k++; 
		Pop(S,&h); 
		printf("%d",h); 
	}
} 
int main() {    
	SqStack S; 
    conversion(&S); 
	printf("\n");  
	return 0;
}

验证

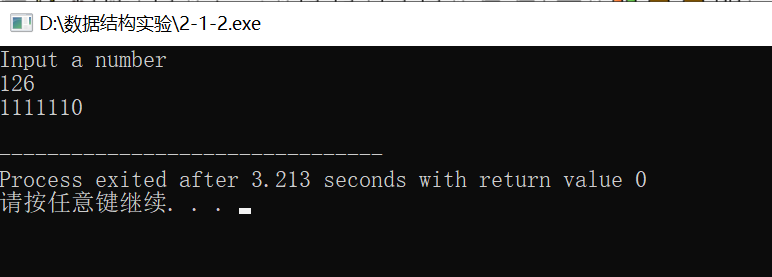
3、阅读并运行程序，并分析程序功能。

#include<stdio.h>
#include<malloc.h>
#include<string.h>
#define M 20
#define  elemtype  char
typedef struct
{
    elemtype stack[M];
    int top;
}
stacknode;
void init(stacknode *st);
void push(stacknode *st,elemtype x);
void pop(stacknode *st);

void init(stacknode *st)
{
    st->top=0;
}

void push(stacknode *st,elemtype x)
{
    if(st->top==M)
        printf("the stack is overflow!\n");
    else
    {
        st->top=st->top+1;
        st->stack[st->top]=x;
    }
}

void pop(stacknode *st)
{
if(st->top>0)  st->top--;
    else  printf(“Stack is Empty!\n”);
}

int main()
{
    char s[M];
    int i;
    stacknode *sp;
    printf("create a empty stack!\n");
    sp= (stacknode*)malloc(sizeof(stacknode));
    init(sp);
    printf("input a expression:\n");
    gets(s);
    for(i=0;i<strlen(s);i++)
    {
        if(s[i]=='(')
            push(sp,s[i]);
        if(s[i]==')')
            pop(sp);
    }
    if(sp->top==0)
        printf("'('match')'!\n");
    else
        printf("'('not match')'!\n");
    return 0;
}

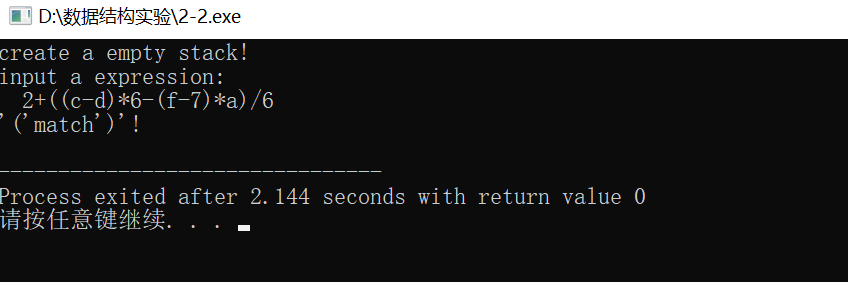
输入：2+((c-d)6-(f-7)a)/6
运行结果：

输入：a-((c-d)*6-(s/3-x)/2
运行结果：

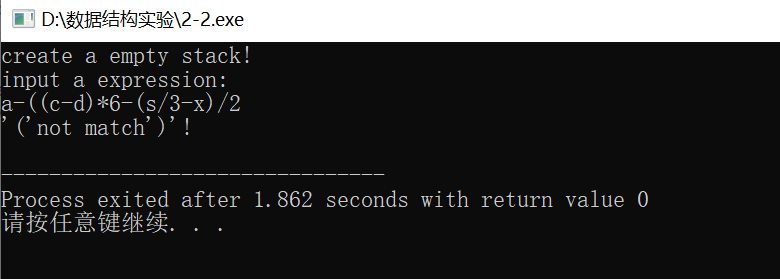
程序的基本功能：
判断一个多项式的左右括号是否匹配。

四、实验小结
通过实验操作对栈与队列有更深的理解，并回顾了栈与队列的基本运算。