字符串匹配
1.RabinKarp
2.KMP
3.前缀树(字典树,Trie);后缀数组
Rabin-Karp算法
题目:假如要判断字符串A"ABA"是不是字符串B"ABABABA"的子串。
解法一:暴力破解法, 直接枚举所有的长度为3的子串,然后依次与A比较,这样就能得出匹配的位置。 这样的时间复杂度是O(M*N),M为B的长度,N为A的长度。
解法二:Rabin-Karp算法
思想:假设待匹配字符串的长度为N,目标字符串的长度为M(M>N);首先计算待匹配字符串的hash值,计算目标字符串前N个字符的hash值;比较前面计算的两个hash值,比较次数M-N+1:若hash值不相等,则继续计算目标字符串的下一个长度为N的字符子串的hash值,若hash值相同,则需要使用比较字符是否相等再次判断是否为相同的子串(这里若hash值相同,则直接可以判断待匹配字符串是目标字符串的子串,之所以需要再次判断字符是否相等,是因为不同的字符计算出来的hash值有可能相等,称之为hash冲突或hash碰撞,不过这是极小的概率,可以忽略不计);
哈希函数定义如下:
其中Cm表示字符串中第m项所代表的特地数字,有很多种定义方法,我习惯于用java自带的char值,也就是ASCII码值。java中的char是16位的,用的Unicode编码,8位的ASCII码包含在Unicode中。b是哈希函数的基数,相当于把字符串看作是b进制数。h是防止哈希值溢出。
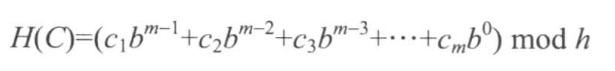
代码:
1 public class RabinKarp {
2
3 public static void main(String[] args) {
4 String s = "ABABABA";
5 String p = "ABA";
6 match(p, s);
7 }
8
9 /**
10 * @param p 模式
11 * @param s 源串
12 */
13 static void match(String p,String s){
14 long hash_p = hash(p);//p的hash值
15 int p_len = p.length();
16 for (int i = 0; i+p_len<= s.length(); i++) {
17 long hash_i = hash(s.substring(i, i+p_len));// i 为起点,长度为p_len的子串的hash值
18 if (hash_p==hash_i) {
19 System.out.println("match:"+i);
20 }
21 }
22 }
23
24 final static long seed = 31; // 进制数
25
26 /**
27 * 不同的字符计算出来的hash值相同 称为hash冲突
28 * 使用100000个不同字符串产生的冲突数,大概在0~3波动,使用100百万不同的字符串,冲突数大概110+范围波动。
29 * @param str
30 * @return
31 */
32 private static long hash(String str) {
33 long h = 0;
34 for (int i = 0; i !=str.length(); i++) {
35 // 这个计算方式就是 An²+Bn+c 的循环表达式,而这个计算方式就是二进制转十进制的计算方式
36 // 这里n=31,可以理解为转为31进制
37 h = seed * h + str.charAt(i);
38
39 }
40 return h%Long.MAX_VALUE; // 防止hash值过大
41 }
42
43 }
结果:
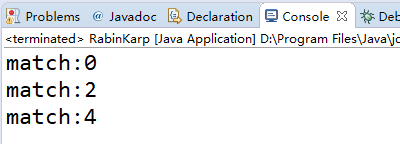
在这里计算一下时间复杂度,计算hash值的时间为O(N),目标字符串长度为M,所以时间复杂度为O(M*N)。好像和暴力破解差不多。下面会通过一种类似于预处理的方式来进行优化,叫做滚动哈希。就是提前计算好源串的hash值,构建成一个hash数组,再通过比较hash值,这样就成功匹配出来了。通过这种优化,时间复杂度下降到O(M+N),O(N)为计算待匹配的字符串计算hash值的时间,O(M)为计算hash数组的时间。
滚动哈希的技巧就是:如果已经算出从k到k+m的子串的哈希值H(S[k,k+1...k+m]),那么从k+1到k+m+1的子串的哈希值就可以基于前一个的哈希值计算得出。
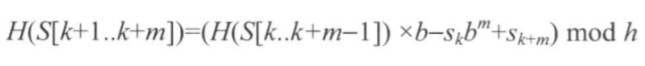
代码:
1 /**
2 * 滚动哈希法
3 * 对目标字符串按d进制求值,mod h 取余作为其hash
4 * 对源串,一次求出m个字符的hash,保存在数组中(滚动计算)
5 * 匹配时,只需对比目标串的hash值和预存的源串的hash值表
6 */
7 public class RabinKarp_1 {
8
9 public static void main(String[] args) {
10 String s = "ABABABA";
11 String p = "ABA";
12 match(p, s);
13 }
14
15 static void match(String p,String s){
16 long hash_p = hash(p);//p的hash值
17 long[] hashOfS = hash(s, p.length());
18 for (int i = 0; i < hashOfS.length; i++) {
19 if (hashOfS[i] == hash_p) {
20 System.out.println("match:" + i);
21 }
22 }
23 }
24
25 final static long seed = 31;
26
27 /**
28 * 滚动哈希
29 * @param s 源串
30 * @param n 子串的长度
31 * @return
32 */
33 private static long[] hash(String s, int n) {
34 long[] res = new long[s.length() - n + 1];
35 //前n个字符的hash
36 res[0] = hash(s.substring(0, n));
37 for (int i = n; i < s.length(); i++) {
38 char newChar = s.charAt(i); // 新增的字符
39 char oldchar = s.charAt(i - n); // 前n字符的第一字符
40 //前n个字符的hash*seed-前n字符的第一字符*seed的n次方
41 long v = (long) ((res[i - n] * seed + newChar - Math.pow(seed, n) * oldchar) % Long.MAX_VALUE);
42 res[i - n + 1] = v;
43 }
44 return res;
45 }
46
47 static long hash(String str) {
48 long h = 0;
49 for (int i = 0; i != str.length(); ++i) {
50 h = seed * h + str.charAt(i);
51 }
52 return h % Long.MAX_VALUE;
53 }
54 }
结果:
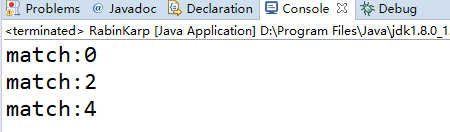
转载:
KMP 算法
public class KmpAlgo { //寻找待匹配串的部分匹配值,放在next数组中 static void getNext(String pattern,int[] next){ int j = 0; int k = -1; next[0] = -1; int len = pattern.length(); while(j < len-1){ if(k == -1 || pattern.charAt(j) == pattern.charAt(j)){ j++; k++; next[j] = k; }else{ k = next[k]; } } } static int kmp(String s,String pattern){ int i = 0; int j = 0; int slen = s.length(); int plen = pattern.length(); int[] next = new int[plen]; getNext(pattern,next); while(i < slen && j < plen){ if(s.charAt(i) == pattern.charAt(j)){ i++; j++; }else if(next[j] == -1){ i++; j = 0; }else{ j = next[j]; } if(j == plen){ return i-j; } } return -1; } /** *@param */ public static void main(String[] args){ String str = "ABCDABDEYGF"; String pat = "ABCDABD"; //KmpAlgo.kmp(str, pat); System.out.println(KmpAlgo.kmp(str, pat)); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号