经典算法案例1 排序--快速排序 &归并排序
快速排序 :
先划分好了 再合并 而快速排序的划分很讲究 所以合并很简单(就是不需要合并就已经有序了的地步) 这点与归元正好相反
我理解的原理:
找到一个中间值 把数组划分为左边是小于等于他的 右边是大于他的
然后再左边递归 右边递归 最后就会变成一个有序的数组 这就是我认为的合并很简单
代码大概是:
private static void quickHelper(int[] array, int left, int right) { if(left >= right){ //此时数组为空,或者只有一个元素不用排序 return; } int index = partition(array,left,right);//第一次划分 返回的index为第一个元码 quickHelper(array,left,index-1);//左边划分 quickHelper(array,index+1,right);//右边划分 }
一遍单向扫描法(主动动的指针只有一个):
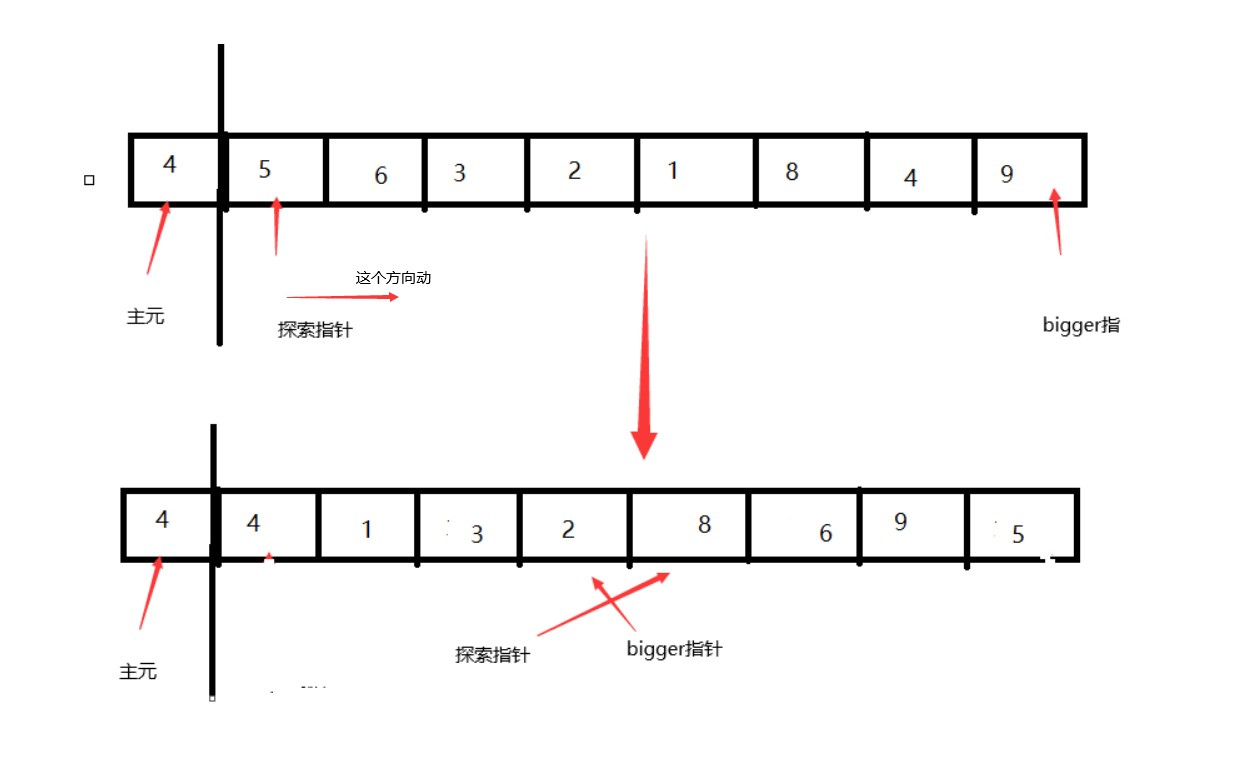
以第一个元素为元码 然后 探索指针为 left 下标为1 bigger指针为right 下标为array.length-1
若探索指针比 元码小 则 left++;
若探索指针比元码大 则 先交换left与right 然后right--;
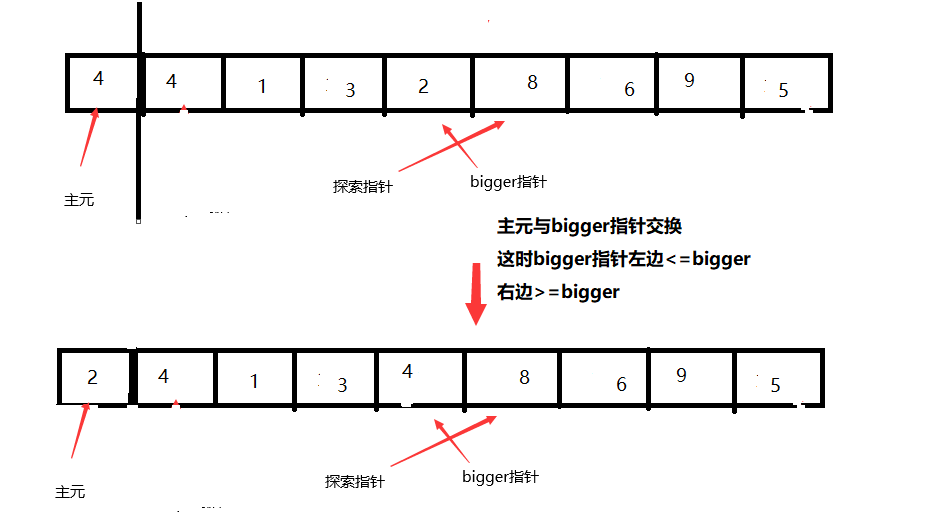
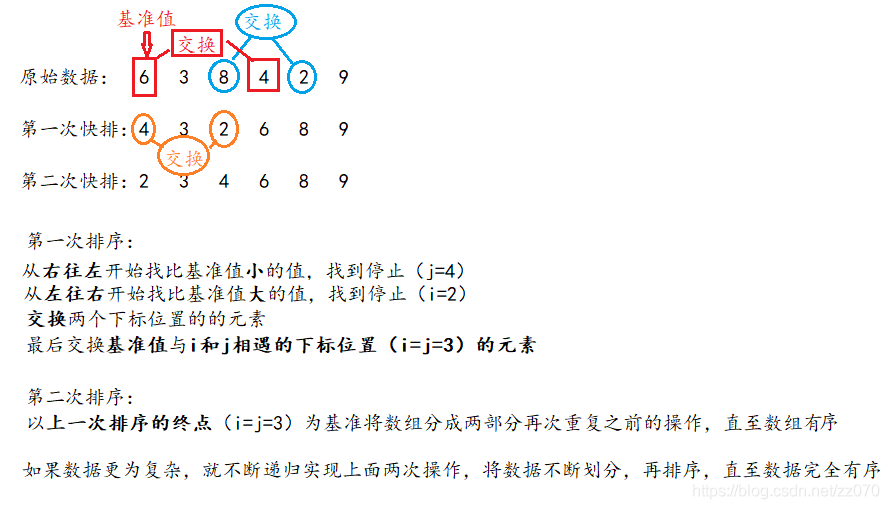
终点就是两个指针交错 如下图:
这时再把right与元码交换即可 这样元码在划分点了 他左边<=他 右边>他
再递归下去即可
left为探索指针 right为bigger指针
/** * @arr 待排序的数组 * @begin 需要partition的起始下标 * @end 需要partition的末尾下标 * @return 返回pivot所在位置下标 */ int partition2(int arr[], int begin, int end){ int pivotIndex = begin; int pivot = arr[pivotIndex]; swap(arr, pivotIndex, end); int big = begin - 1; // index of smaller element for (int small = begin; small <= end - 1; small++){ // 遇到一个元素小于pivot if (arr[small] <= pivot){ big++; swap(arr, big, small); } } swap(arr, big + 1, end); return big + 1; }
双指针扫描法(两个指针一起动):
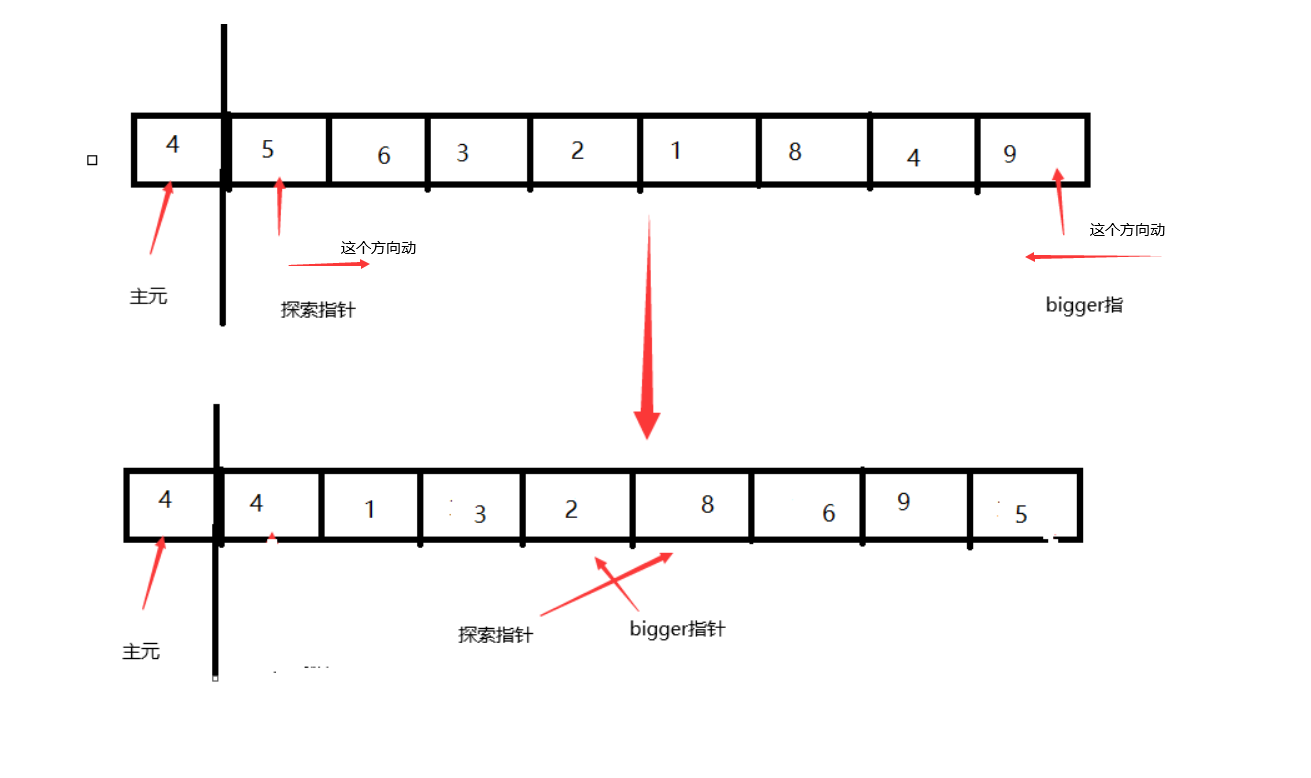
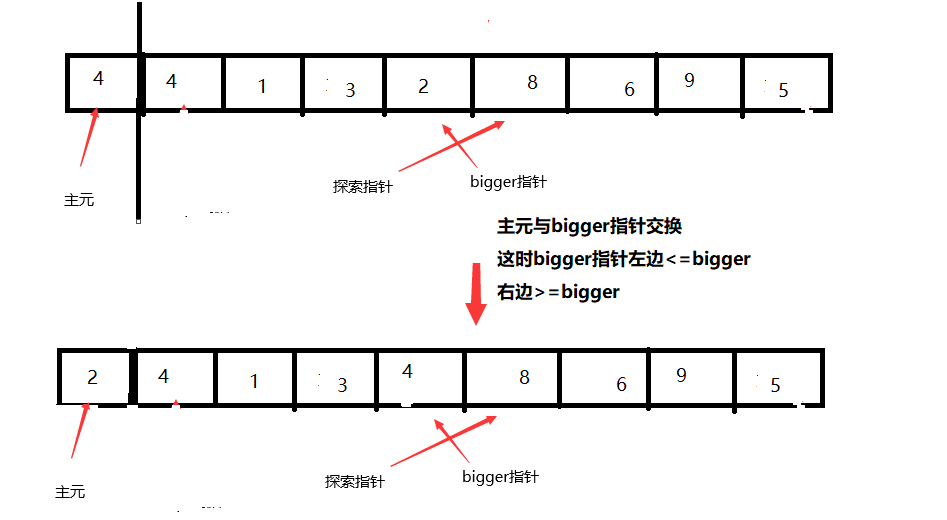
同样的3个指针分布
单指针只是左边走 而右边只用来交换
而双指针则是一起走的 left<=主元时 一直++ 直到停下来
right<主元时 一直++ 直到停下来
public class selectK { public static void main(String[] args) { int[] a = {4,2,3,5}; quicksort(a,0,3); for(int x:a){ System.out.println(x); } int b = select(a,0,a.length-1,2); System.out.println(b); } public static void quicksort(int[] a,int p,int r){ if(p<r){ int q =partition2(a,p,r); quicksort(a,p,q-1); quicksort(a,q+1,r); } } //双指针遍历交换 分区 public static int partition2(int[] a,int p,int r){ int pivot = a[p]; int left = p+1;//扫描指针 int right = r;//右侧指针 while (left <= right){ while (left <= right && a[left] <= pivot) left++; while (left <= right && a[left] > pivot) right--; if (left < right){ swap(a,left,right); } } swap(a,p,right); return right; } //交换函数 public static void swap(int[] a,int p,int r){ int temp = a[p]; a[p]=a[r]; a[r]=temp; } }
算法优化
- 在递归到规模比较小时,使用选择排序/插入排序代替。
- 选取一个比较靠谱的pivot。(取first,取last,取middle,取三者的中)
- 使用循环代替递归。
归并排序 :
/** * 归并排序: * 把数组分成两部分。每两部分再分成两部分排序,递归。 * 一直分成每部分只有一个元素。 * 再合并。就变成整体有序了。 * * * 时间复杂度:O(nlogn) * 空间复杂度:O(N),归并排序需要一个与原数组相同长度的数组做辅助来排序 * 稳定性:归并排序是稳定的排序算法,temp[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++]; * 这行代码可以保证当左右两部分的值相等的时候,先复制左边的值,这样可以保证值相等的时候两个元素的相对位置不变。 * * @param arr */ public static void guibingSort(int[] arr) { sort(arr, 0, arr.length-1); } public static void sort(int[] arr, int left, int right){ if(left == right){ return; } int mid = left + ((right - left) >> 1); sort(arr,left,mid); sort(arr,mid+1,right); merge(arr,left,mid,right); } /** * 将两个分离开数组合并 * @param arr * @param left * @param mid * @param right */ public static void merge(int[] arr, int left, int mid, int right) { int[] tmp = new int[right - left + 1]; int i = 0; int p1 = left; int p2 = mid + 1; // 比较左右两边的数据,小的放在tmp里面 while (p1 <= mid && p2 <= right) { if (arr[p1] < arr[p2]) { tmp[i++] = arr[p1++]; } else { tmp[i++] = arr[p2++]; } // 人家的写法,也就是用了一个三目运算 // tmp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; } // 循环结束后。吧另外一个剩下的全部插入到临时数组后面 while (p1 <= mid) { tmp[i++] = arr[p1++]; } while (p2 <= right) { tmp[i++] = arr[p2++]; } // 把合并好的数组放回原来的数组 for (int j = 0; j < tmp.length; j++) { arr[left + j] = tmp[j]; } }
算法案例
➢调整数组顺序使奇数位于偶数前面:输入-个整数数组,调整数组 中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。要求时间复杂度为O(n).
快排思路 -》以及这里使用了双指针
package algorithm.foroffer.top20; import java.util.Arrays; /** * Created by liyazhou on 2017/5/26. * 面试题14:调整数组顺序使奇数位于偶数前面 * 题目: * 输入一个整数数组,实现一个函数来调整该数组中数字的顺序, * 使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。 * * 问题: * 1. 排序 * * 思路: * 1. 快速排序的思想 * 2. 用 A、B 两个指针分别指向数组的开始和末尾 * A 指针往右移动,若发现偶数则停止移动 * B 指针往左移动,若发现奇数则停止移动 * 若 A 指向偶数,B 指向奇数。交换两者的位置 * 直到 A、B 指针相遇 * */ public class Test14 { public static void reorderOddEven(int[] array){ if (array == null) return; int first = 0; int second = array.length-1; while (first < second){ // 从左往右,找到第一个偶数 while(((array[first] & 1) == 1) && first < second) first ++; while(((array[second] & 1) == 0) && second > first) second --; // 从右往左,找到第一个奇数 if (first < second){ int tmp = array[first]; array[first] = array[second]; array[second] = tmp; } } } public static void main(String[] args){ int[] array = {1, 2 ,3, 4, 5, 6, 7, 8, 9, 10}; System.out.println(Arrays.toString(array)); Test14.reorderOddEven(array); System.out.println(Arrays.toString(array)); } }
➢第k个元素;以尽量高的效率求出一个乱序数组中按数值顺序的第K个元素值
13495 k=3 则输出5
快排划分思路 ——》快排划分了会这样 小于元码有3个 元码 大于元码有5个 那么第4个元素就是元码 那假如我要找第2个呢 那2<元码下标+1 我是不是要在左边找 要找第5个就在右边找 这样递归下去
public static int select(int[] a,int p,int r,int k)就是了 调用了快排的划分
public class selectK { public static void main(String[] args) { int[] a = {4,2,3,5}; quicksort(a,0,3); for(int x:a){ System.out.println(x); } int b = select(a,0,a.length-1,2); System.out.println(b); } /* @param arr数组 p探索指针 r最右侧指针 k按顺序的第几个数 //第k个元素;以尽量高的效率求出一个乱序数组中按数值顺序的第 //K个元素值 */ public static int select(int[] a,int p,int r,int k){ int q = partition2(a,p,r);//主元下标 用快排 int qK = q - p + 1;//主元是第几(k)个元素 if (qK ==k) return a[q]; else if(k<qK)return select( a, p,q-1, k); else return select(a,q+1,r,k-qK);//这里的k是重新算的 }
//这个是快排 public static void quicksort(int[] a,int p,int r){ if(p<r){ int q =partition2(a,p,r); quicksort(a,p,q-1); quicksort(a,q+1,r); } } //双指针遍历交换 分区 public static int partition2(int[] a,int p,int r){ int pivot = a[p]; int left = p+1;//扫描指针 int right = r;//右侧指针 while (left <= right){ while (left <= right && a[left] <= pivot) left++; while (left <= right && a[left] > pivot) right--; if (left < right){ swap(a,left,right); } } swap(a,p,right); return right; } //交换函数 public static void swap(int[] a,int p,int r){ int temp = a[p]; a[p]=a[r]; a[r]=temp; } }
➢超过一半的数字:数组中有一个数字出现的次数超过了数组长度的-半,找出这个数字。
➢最小可用ID :在非负数组(乱序)中找到最小的可分配的id (从1开始编号) ,数据量1000000
2道逆序对的题目
➢合并有序数组∶给定两个排序后的数组A和B,其中A的末端有足够
的缓冲空间容纳B。编写一个方法,将B合并入A并排序
思路:3个指针 过龙门的方式即可 A12389指针1- - -门current指针3
B234指针2
➢逆序对个数︰一个数列,如果左边的数大,右边的数小,则称这
两个数位一个逆序对。求出一个数列中有多少个逆序对。
归并


 浙公网安备 33010602011771号
浙公网安备 33010602011771号