(210周赛)5536. 最大网络秩

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。

两座不同城市构成的 城市对 的 网络秩 定义为：与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算 一次 。

整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的 最大网络秩 。

示例 1：

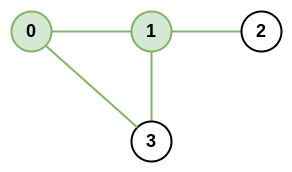
输入：n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出：4
解释：城市 0 和 1 的网络秩是 4，因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。

示例 2：

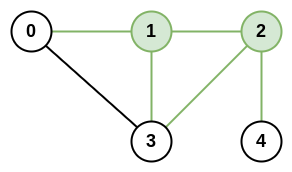
输入：n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
输出：5
解释：共有 5 条道路与城市 1 或 2 相连。

示例 3：

输入：n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
输出：5
解释：2 和 5 的网络秩为 5，注意并非所有的城市都需要连接起来。

提示：

2 <= n <= 100
0 <= roads.length <= n * (n - 1) / 2
roads[i].length == 2
0 <= ai, bi <= n-1
ai != bi
每对城市之间 最多只有一条 道路相连

 

思路：

参考：https://leetcode-cn.com/problems/maximal-network-rank/solution/jian-dan-de-mei-ju-by-lucifer1004/

题目可以理解为图中任意找出两个点，以其中至少一个为端点的不重复的边的数目的最大值是多少？

首先把边集转为邻接表，然后枚举即可。我们可以先确定一个点，然后首先枚举与其邻接的点（结果需要减去1以去重）；然后枚举剩余的点（结果不需要去重）。

总时间复杂度O(N^2)。

class Solution {
public:
    int maximalNetworkRank(int n, vector<vector<int>>& roads) {
        int res = 0;
        vector<vector<int> > adj(n);
        for(auto road:roads){
            adj[road[0]].push_back(road[1]);
            adj[road[1]].push_back(road[0]);
        }
        for(int i=0;i<n;i++){
            vector<bool> v(n);
            for(auto j:adj[i]){
                res = max(res,(int)adj[i].size() + (int)adj[j].size() - 1);
                v[j] = true;
            }
            for(int j=i+1;j<n;j++)
                if(!v[j])
                    res = max(res,(int)adj[i].size() + (int)adj[j].size());
        }
        return res;
    }
};