CF1695C Zero Path

给定一个 \(n\times m\) 的矩阵，元素 \(a_{i,j}\in\{1,-1\}\)。只能向下或向右走，判定是否存在一条从 \((1,1)\) 到 \((n,m)\) 的路径，走过的元素和为 \(0\)。\(n,m\le 1000\)。

首先，如果路径长度 \(n+m-1\) 是奇数，则一定无解。因为这时要么走奇数个 \(1\) 偶数个 \(-1\)，要么走奇数个 \(-1\) 偶数个 \(1\)，最后的和一定是奇数，不可能是 \(0\)。

对于路径和是偶数的情况，有这样的性质：设 \(f_{i,j}\) 表示从 \((1,1)\) 走到 \((i,j)\) 的最大路径和，\(g_{i,j}\) 表示最小路径和。如果 \(f_{i,j}\ge 0, g_{i,j}\le 0\)，则从 \((1,1)\) 到 \((i,j)\) 一定存在一条和为 \(0\) 的路径。

这是为什么呢？我们可以写出从 \((1,1)\) 走到 \((i,j)\) 的操作序列，\(\texttt{R}\) 代表向右走一步，\(\texttt{D}\) 代表向下走一步。以下图为例，可以写成 \(\texttt{RDRRD}\)。显然，走到 \((i,j)\) 的操作序列，尽管顺序不同，但都是 \(i-1\) 个 \(\texttt{R}\) 和 \(j-1\) 个 \(\texttt{D}\)。

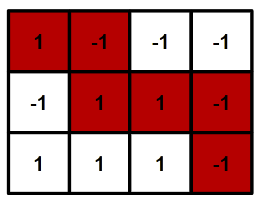
要得到另一条走到 \((i,j)\) 的路径，我们可以多次交换操作序列里相邻的字母。如果两个字母相同，交换它们没有意义，所以我们只考虑相邻字母不同的交换。如下图所示，当我们交换一对 \(\texttt{R,D}\) 时，我们把一个格子 \((2,2)\) 从路径中删去，加入一个新的格子 \((1,3)\)。此时路径和的变化可能是 \(-2,0,2\) 中的一个。如果最小路径可以一个 \(2\) 一个 \(2\) 的换成最大路径，则一定可以构造出一条和为 \(0\) 的路径。得证。

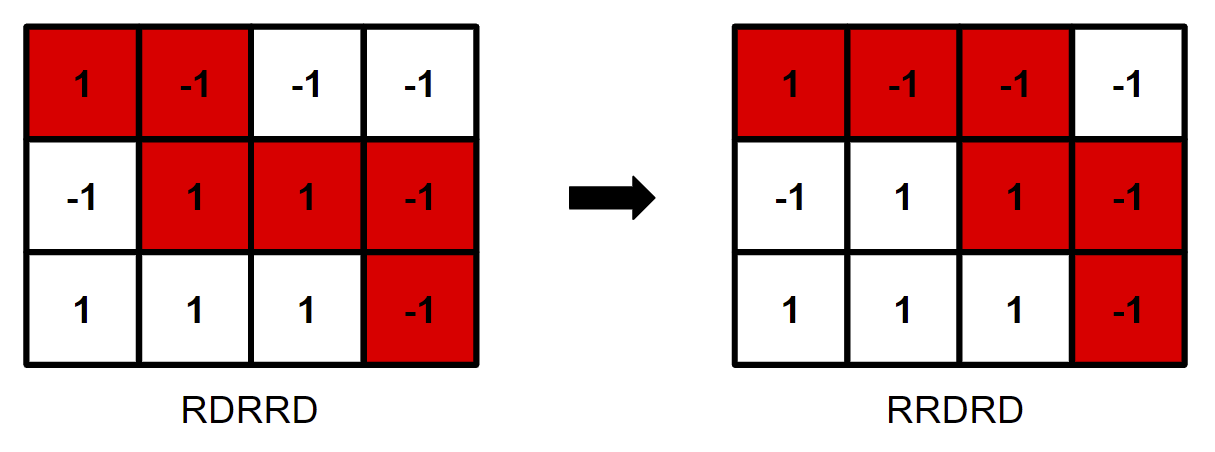
所以，基于上述性质，我们可以用 \(O(nm)\) 的 dp 计算出 \(f,g\)（注意处理边界情况），然后判断 f[n][m] >= 0 && g[n][m] <= 0 输出答案。转移方程是：

• \(f_{i,j}=\max(f_{i-1,j},f_{i,j-1})+a_{i,j}\)
• \(g_{i,j}=\min(g_{i-1,j},g_{i,j-1})+a_{i,j}\)

下面是 AC 代码：

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
        }
    }
    if ((n + m) % 2 == 0) {
        cout << "NO\n";
        return;
    }
    for (int i = 2; i <= max(n, m); i++) {
        f[i][0] = f[0][i] = -INF;
        g[i][0] = g[0][i] = INF;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j];
            g[i][j] = min(g[i - 1][j], g[i][j - 1]) + a[i][j];
        }
    }
    if (f[n][m] >= 0 && g[n][m] <= 0) {
        cout << "YES\n";
    } else {
        cout << "NO\n";
    }
}