CF2048E Kevin and Bipartite Graph
“同种颜色的边不成环”可以等价转化为“同种颜色的边构成森林”,所以同种颜色的边最多 \(2n+m-1\) 条。总共有 \(n\) 种颜色,所以合法的最大边数为 \((2n+m-1)n\)。 有解条件 \((2n+m-1)n\ge 2nm\),化简得 \(m\le 2n-1\)。
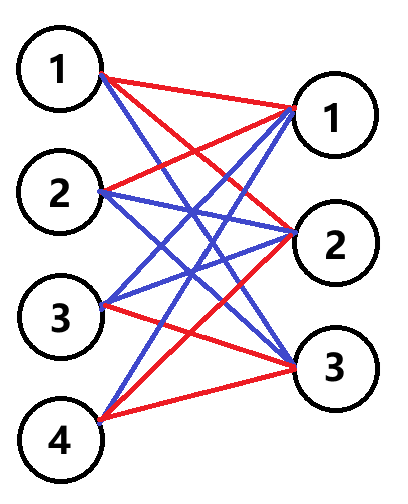
处理完了无解情况,下面来设计构造方案。注意到同种颜色可以左右交替连接成一条链,如图所示。
“同种颜色的边不成环”可以等价转化为“同种颜色的边构成森林”,所以同种颜色的边最多 \(2n+m-1\) 条。总共有 \(n\) 种颜色,所以合法的最大边数为 \((2n+m-1)n\)。 有解条件 \((2n+m-1)n\ge 2nm\),化简得 \(m\le 2n-1\)。
处理完了无解情况,下面来设计构造方案。注意到同种颜色可以左右交替连接成一条链,如图所示。

