大学物理期末复习

电场

一、公式

• 静电力计算：库伦定律 \(\vec{F}=\dfrac{q_1q_2}{4\pi \epsilon_0 r^2}\vec{e_r}\)
• 电场强度：\(\vec{E}=\dfrac{\vec{F}}{q_0}=\dfrac{q}{4\pi \epsilon_0 r^2}\vec{e_r}\)
• 电通量：\(\Phi_e=\vec{E}\cdot\vec{S}\)，规定穿出闭合曲面为正，穿入闭合曲面为负
• 高斯定理： 通过封闭曲面（高斯面）的电通量 \(\oint_L \vec{E}\cdot\vec{S}=\dfrac{1}{\epsilon_0}\sum q_{内}\)，静电场是有源场
• 静电场环路定理：任意 闭合路径 总场强为 0，\(\oint_L\vec{E}\cdot d\vec{l}=0\)，静电场是保守场
• 电势：\(U_p=\int_p\vec{E}\cdot d\vec{l}=\dfrac{W_p}{q_0}\)
• 电势差 \(U_{ab}=U_a-U_b=\int_a^b\vec{E}\cdot d\vec{l}\)，静电力做功 \(A_{ab}=qU_{ab}\)
• 点电荷电场中的电势：\(U=\dfrac{q}{4\pi\epsilon_0 r}\)

二、题型

• 点电荷系场强计算：叠加 \(\sum\)
• 带电体场强计算：积分 \(\int\)；找高斯面用定理（带电球壳、带电球体等）
  • 带电球壳：\(E=\dfrac{qx}{4\pi\epsilon_0 (x^2+R^2)^\frac{3}{2}}\)
  • 带电球体：\(E=\dfrac{q}{2\pi\epsilon_0R}(1-\dfrac{x}{\sqrt{x^2+R^2}})\)
• 无限大平面场强：圆柱体形高斯面，计算得 \(\dfrac{\sigma}{2\epsilon_0}\)，其中 \(\sigma\) 为电荷面密度，\(\epsilon_0\) 为真空介电常数

• 带电体电势计算

波动光学

一、光的干涉

干涉条件：①频率相同；②存在平行的光振动分量；③相位差恒定

1. 光程

• 单色光在某种介质内的速度为 \(u\)，则有 \(n=\dfrac{c}{u}\)
• 前进距离为 \(d\)，光程为 \(nd\)（相同时间在真空中能走的距离）
• 透镜不产生光程差
• 光程差与相位差的关系：\(\Delta\phi=\dfrac{2\pi}{\lambda_n}(r_2-r_1),n\lambda_n=\lambda\)，所以 \(\Delta\phi=2\pi\dfrac{\delta_光}{\lambda}\)

2. 杨氏双缝干涉实验

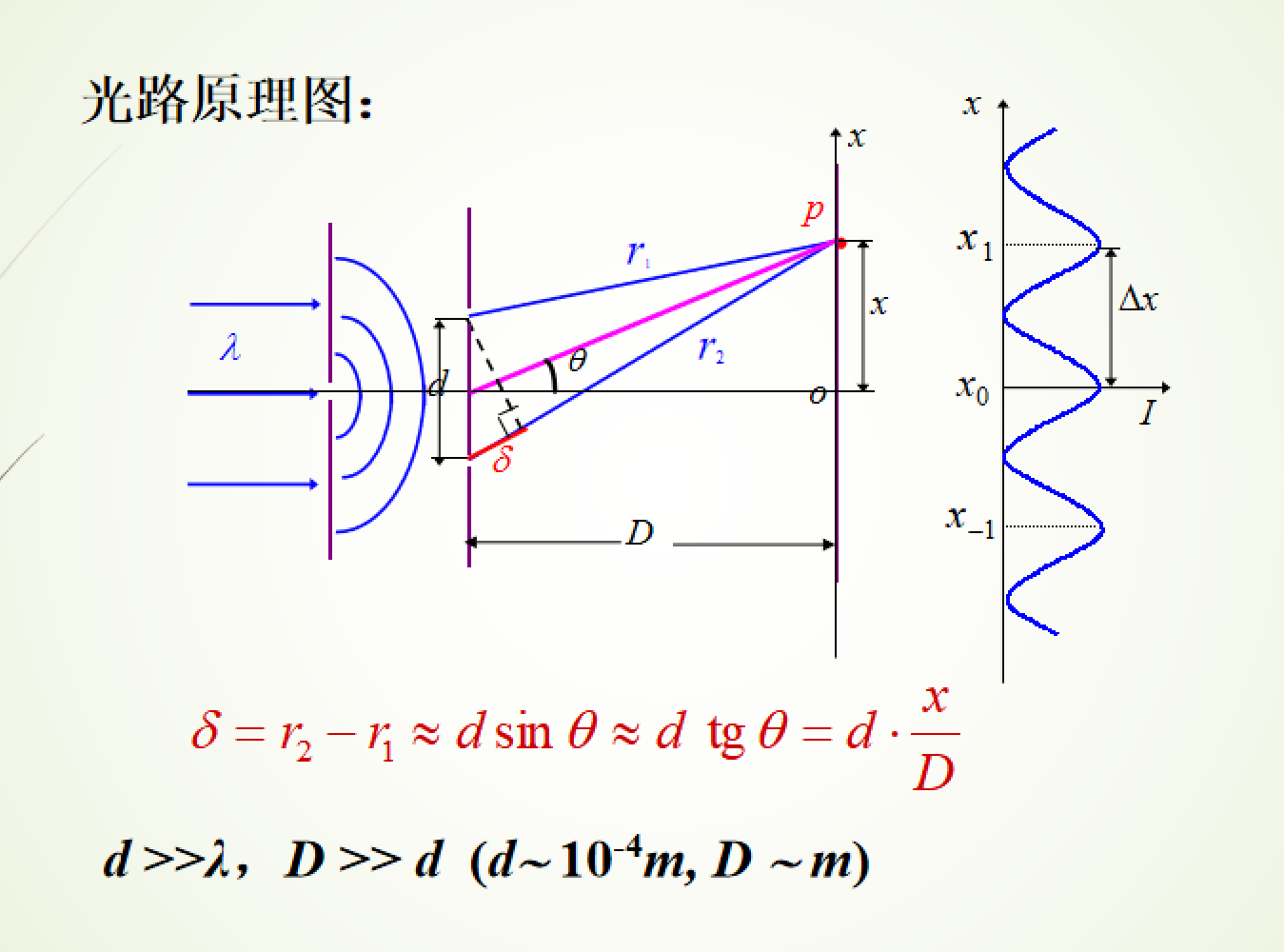
• 明条纹：\(d\dfrac{x}{D}=\pm k\lambda, x=\pm\dfrac{kD\lambda}{d}\)
• 暗条纹：\(d\dfrac{x}{D}=\pm(2k-1)\dfrac{\lambda}{2},x=\pm\dfrac{(2k-1)D\lambda}{2d}\)
• 相邻明条纹（暗条纹）间距：\(\Delta x=x_{k+1}-x_k=\dfrac{D}{d}\lambda\)，\(\Delta x\) 正比于 \(\lambda\)
• 各级明条纹间距相等，光强相等

加盖玻璃片时：

• 盖住上缝—— \(\delta=r_2-(r_1-e+ne)\) 中央明纹上移
• 盖住下缝—— \(\delta=(r_2-e+ne)-r_1\) 中央明纹下移

用厚度为 \(e\)，折射率为 \(n\) 的玻璃片加盖一缝，零级明纹移动到原来的第几级明纹处？
覆盖后零级明纹 \(\delta=r_2-(r_1-e+ne)=0\)，覆盖前 \(k\) 级明纹有 \(r_2-r_1=k\lambda\)，所以 \((n-1)e=k\lambda\)

移动光源时：

• 上移光源—— \(\delta=d\sin\alpha+d\sin\theta\) 中央明纹下移
• 下移光源—— \(\delta=d\sin\alpha-d\sin\theta\) 中央明纹上移

劳埃德镜

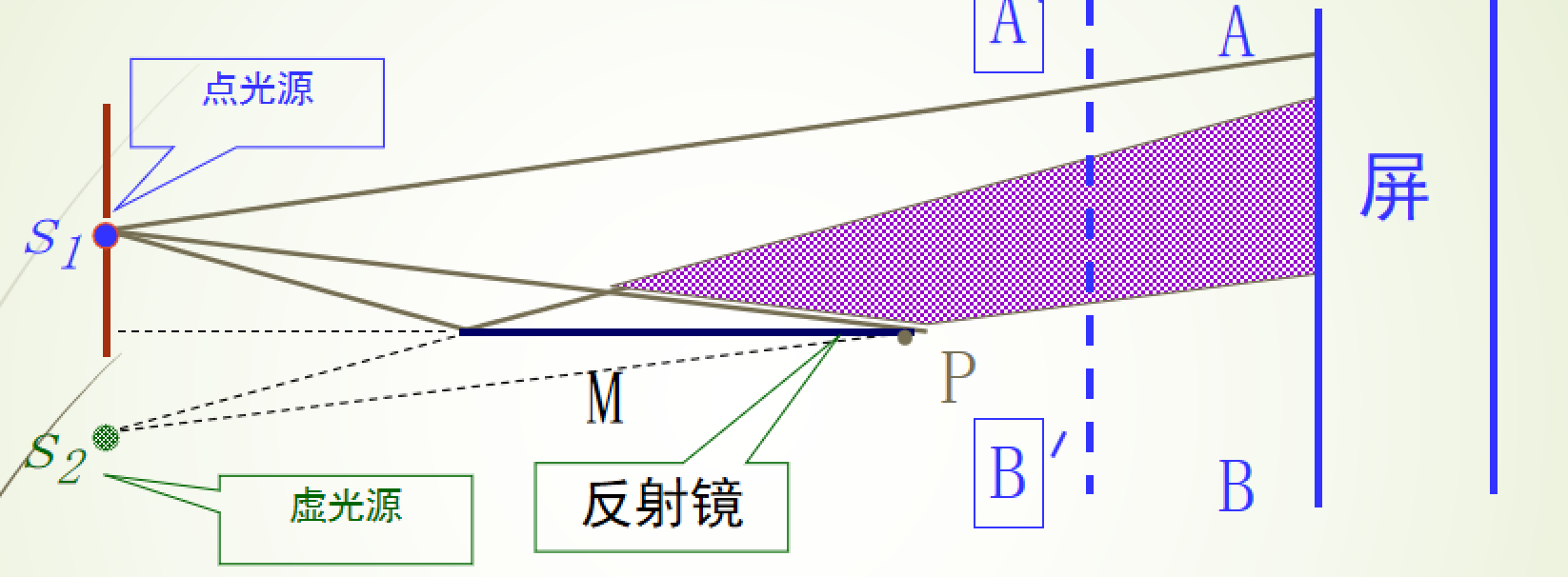
画出虚光源，类比双缝干涉

3. 半波损失

光疏介质到光密介质，垂直入射或者掠入射时，反射波发生半波损失，相当于多走（少走） \(\dfrac{\lambda}{2}\)

4. 薄膜干涉

• 干涉加强：\(\delta=2e\sqrt{n_2^2-n_1^2\sin^2i}+\delta'=k\lambda\)
• 干涉减弱：\(\delta=2e\sqrt{n_2^2-n_1^2\sin^2i}+\delta'=(2k+1)\dfrac{\lambda}{2}\)

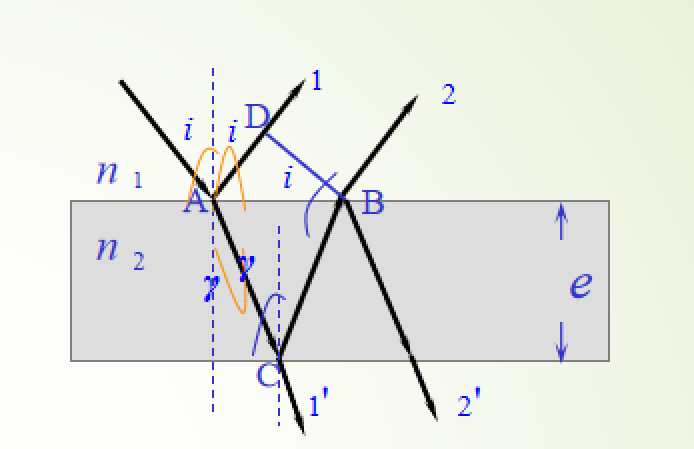
\(\delta'\) 表示有无半波损失，实际上只有中间介质 \(n_2\) 最大或最小时有半波损失

增透膜：用干涉减弱反射
增反膜：用干涉加强反射

5. 劈尖干涉

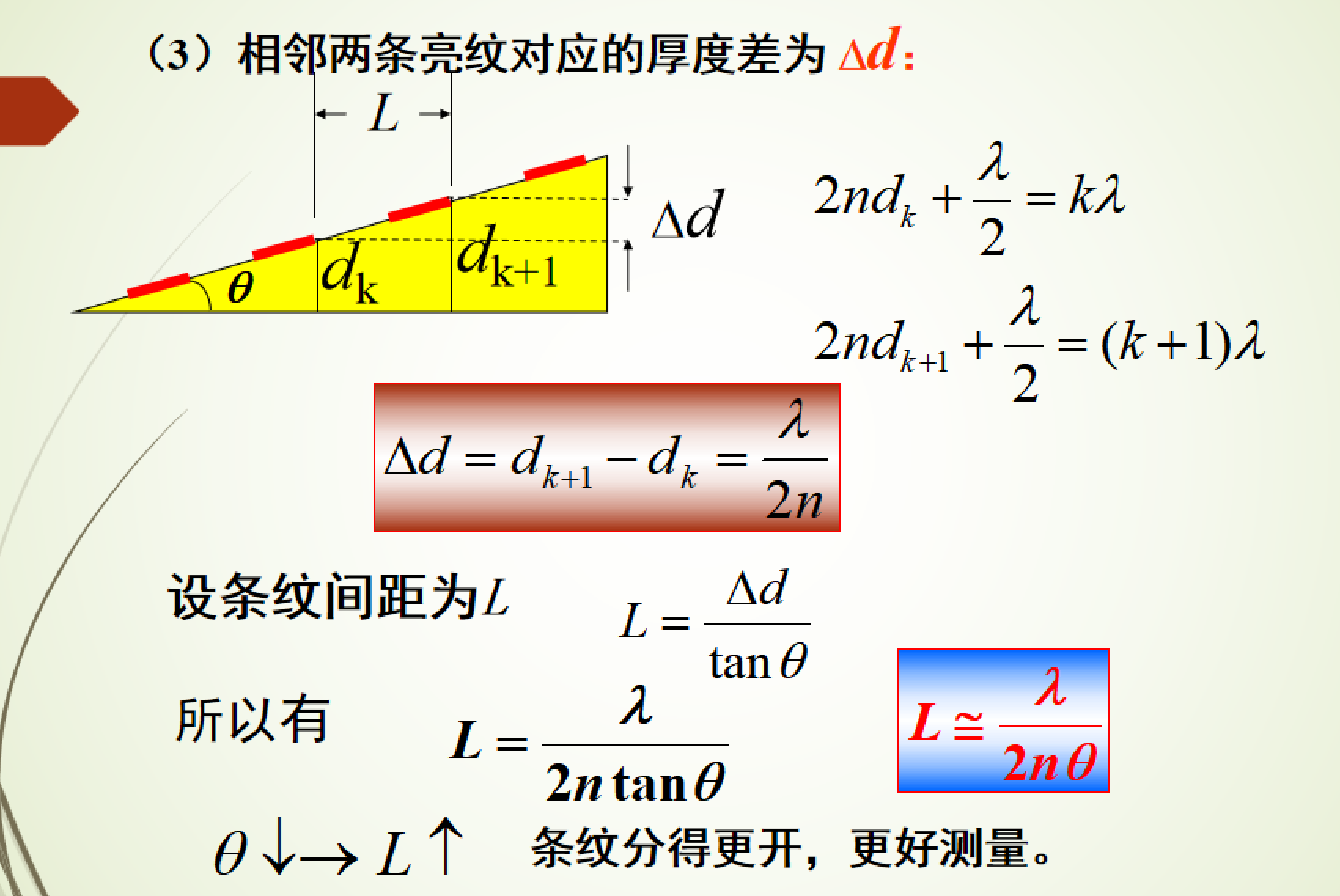
• 利用劈尖可以测量微小角度、微小厚度及照射光波长
• 空气劈尖在尖端是暗纹

牛顿环

• 明环：\(r=\sqrt{(k-\dfrac{1}{2})\dfrac{R\lambda}{n}}\)
• 暗环：\(r=\sqrt{\dfrac{kR\lambda}{n}}\)
• 中心为暗环，从里向外越来越密

二、光的衍射

光偏离直线传播的现象成为衍射。当障碍物的大小和光的波长可比时，发生衍射。

1. 夫琅禾费衍射

光源、光屏与衍射孔三者间的距离皆为无限远，或相当于无限远的衍射

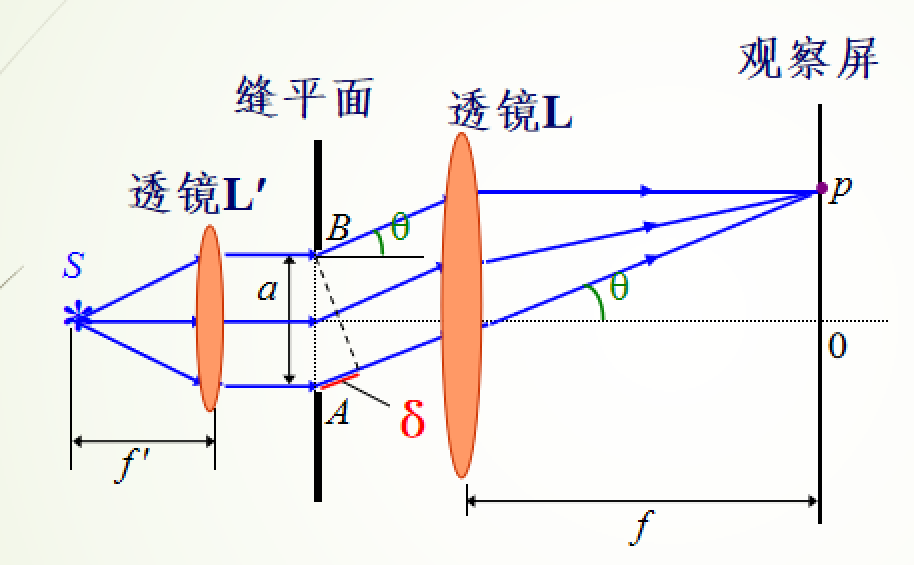
最大光程差 \(\delta=a\sin\theta\)，根据菲涅尔半波带法：

1. \(\theta=0\) 时，所有平行光束相位相同，中央明纹
2. \(a\sin\theta=\pm 2k\dfrac{\lambda}{2}\) 暗纹（互相抵消）
3. \(a\sin\theta=\pm (2k+1)\dfrac{\lambda}{2}\) 明纹 （剩一个）
4. 中央明纹最亮，其余依次减弱

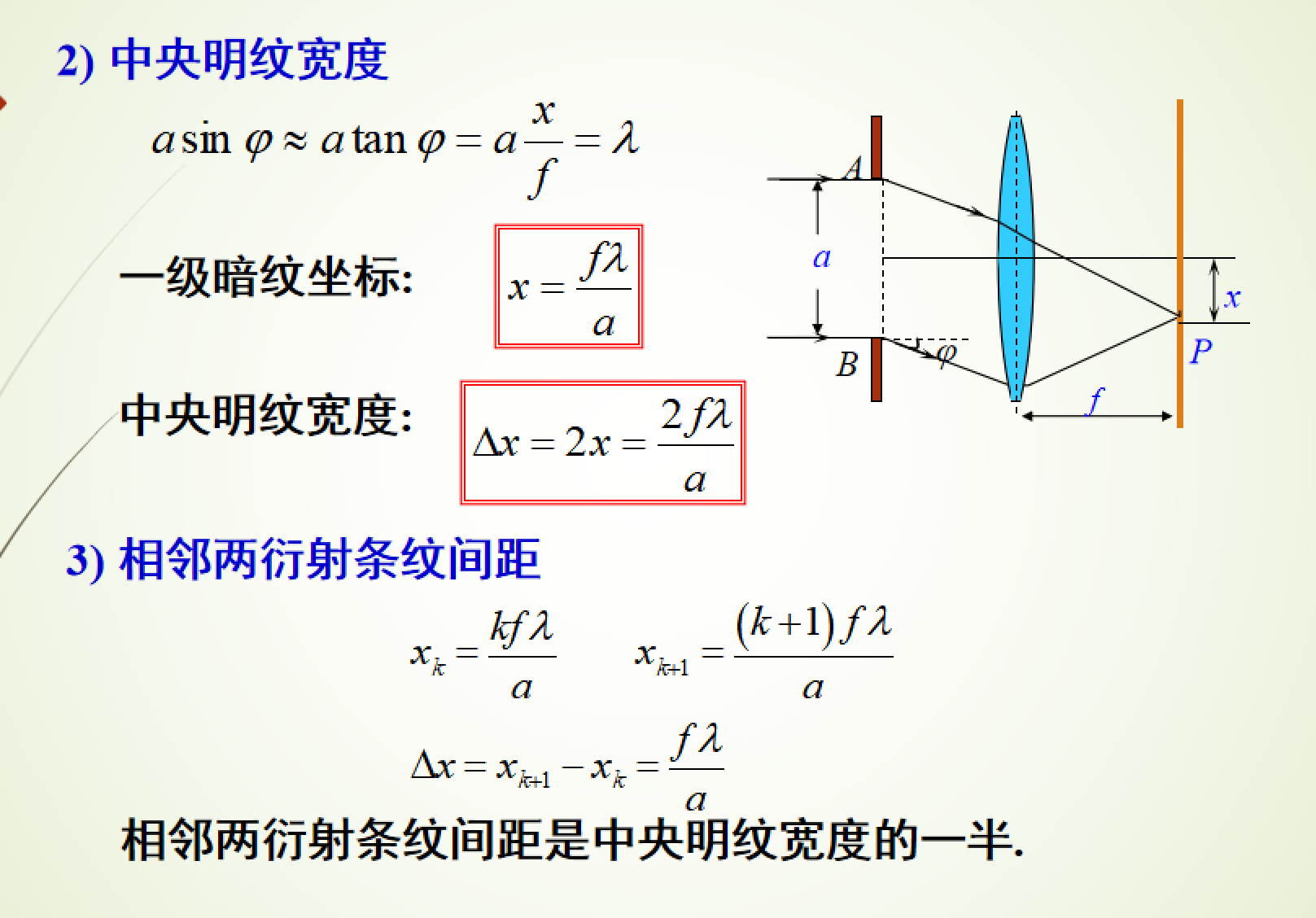
所以非中央明纹宽度和暗纹宽度也是 \(\dfrac{f\lambda}{a}\)，相邻明纹的角宽度是 \(\Delta\phi=\dfrac{\lambda}{a}\)

2. 光栅衍射

三、光的偏振