"蔚来杯"2022牛客暑期多校训练营5

	A	B	C	D	E	F	G	H	I	J	K
赛时过题		O	O	O		O	O	O			O
赛后补题	O

赛后总结：

这场比赛出了很多锅，几乎所有题题意都有问题，甚至有的题std都是错的，数据也是错的。。。

不过还是有几道好题的。

比如说A题，非常可惜比赛的时候没做出来，实际上排个序以后就有很优秀的性质了，之前也有好多题排个序就有很优秀的性质了。

因此目前我总结了三大做题法宝：逆向思维、简化问题、排序数列

赛时排名：（由于本场比赛出了非常多锅，改为unrated，很多人比到一半就退赛了，所以排名仅供参考）

可能还是校内排名更有价值。我们队校内排名8/20，有6个队都是8题，就比我们多过了A题。。。亏大了

K Headphones

题目难度：check-in

题目大意：有N对耳机，Yasa拿出正好k对，NIO至少要取出多少只，能够比Yasa取出的多。耳机左右为一对，Yasa拿出的都是一对，NIO要取的是一只一只的。

解题思路：鸽巢原理，最坏情况下NIO拿到的耳机全是单只的，只要判断一下NIO要拿的个数是否已经超过剩下的耳机对数就行。

参考代码：

查看代码

 #include<iostream>
#include<cstdio>
int main()
{
    int n,k;scanf("%d%d",&n,&k);n-=k;
    if (n<=k) return printf("-1\n"),0;
    printf("%d\n",n+k+1);
    return 0;
}

C Headphones

题目难度：easy

题目大意：有个01组成的字符串，对某些位置询问是否是1 共询问3n次

至多一次询问会返回错误答案，问这些询问结果能否唯一确定字符串

解题思路：

记录每一位上被问过的YES/NO次数，分类讨论。

1、首先如果存在不被问到的位置，输出-1（这一位无法唯一确定）

2、我们判断下是否存在YES和NO均出现过的位置，假设共出现x次

①如果x>1，输出-1；（有多个询问返回错误答案，没有合法字符串）

②如果x=1，表明错误位置确定

如果某一位YES/NO次数都为1，输出-1（这一位无法唯一确定）

如果某一位YES/NO次数均大于1，输出-1（有多个询问返回错误答案，没有合法字符串）

如果某一位YES/NO次数一个为1一个大于1，则可唯一确定

③如果x=0，那么我们判断下是否存在YES和NO总共出现1次的位置，则这一位无法唯一确定，否则则能够唯一确定字符串

参考代码：

查看代码

 /*#if(__cplusplus == 201103L)
#include <unordered_map>
#include <unordered_set>
#else
#include <tr1/unordered_map>
#include <tr1/unordered_set>
namespace std
{
    using std::tr1::unordered_map;
    using std::tr1::unordered_set;
}
#endif*/
#include<bits/stdc++.h>
using namespace std;
int n,num[200000][5],cnt;
char ch[200];
int main()
{
while(scanf("%d",&n)!=EOF)
{
	bool flag=1;
	for(int i=0;i<=n;i++)
	num[i][0]=num[i][1]=0;
	for(int i=1;i<=3*n;i++)
	{
		int x;
		scanf("%d%s",&x,ch+1);
		if(ch[1]=='Y')
		{
			num[x][1]++;
		}
		else
		{
			num[x][0]++;
		}
	}
	for(int i=0;i<n;i++)
	{
		if(num[i][1]==0&&num[i][0]==0)
		{
			cout<<"-1"<<endl;
			flag=0;
			break;
		}
	}
	if(!flag)
	continue;
	int pos;
	for(int i=0;i<n;i++)
	{
		if(num[i][1]&&num[i][0])
		{
			cnt++;
			pos=i;
		}
	}
	if(cnt>=2)
	{
		cout<<"-1"<<endl;
		continue;
	}
	if(cnt==0)
	{
		for(int i=0;i<n;i++)
		{
			if(num[i][1]+num[i][0]==1)
			{
				cout<<"-1"<<endl;
				flag=0;
				break;
			}
		}
		if(flag==0) continue;
		for(int i=0;i<n;i++)
		{
			if(num[i][1])
			printf("1");
			else
			printf("0");
		}
		puts("");
		return 0;
	}
	else
	{
		if((num[pos][1]>1&&num[pos][0]>1)||(num[pos][1]==1&&num[pos][0]==1))
		{
			printf("-1\n");
			continue;
		}
		for(int i=0;i<n;i++)
		{
			if(i==pos)
			{
				if(num[pos][1]>1)
				printf("1");
				else
				printf("0");
			}
			else
			{
				if(num[i][1])
				printf("1");
				else
				printf("0");
			}
		}
		puts("");
		return 0;
	}
}
	return 0;
 }
/*
3
0 NO
1 NO
2 YES
0 YES
1 NO
2 YES
0 YES
1 NO
2 YES
*/

B Watches

题目难度：easy

题目大意：给定n(1e5)件商品的价格，如果你选购k件商品，那么购买原序列中第i件物品的花费就是ai+k*i，问最多能买多少件

解题思路：

注意到答案具有单调性，考虑二分答案k

则问题变为判定是否能选择k件物品，总花费不超过M元，直接贪心即可

赛时情况：

这啥垃圾题意，也没说相同物品能否取多次。。。丁老师猜每个物品只能取一次，然后确实如此。

实际上相同物品能取多次的话也能做，也是贪心，不过不是选前k个ai+k*i最小的物品，而是ai+k*i最小的物品选k次了。

参考代码：

查看代码

 #include<iostream>
#include<cstdio>
#include<algorithm>
#define For(i,a,b) for(int i=a;i<=b;i++)
const int N=1e5+1000;
struct DATA
{
    long long v,id;
}s[N];
long long k,n,m;
int cmp(const DATA&a,const DATA&b)
{
    return a.v+a.id*k<b.v+b.id*k;
}
int check(long long x)
{
    k=x;std::sort(s+1,s+1+n,cmp);
    long long sum=0;
    For(i,1,k) sum+=s[i].v+s[i].id*k;
    return sum<=m;
}
int main()
{
    scanf("%lld%lld",&n,&m);
    For(i,1,n) scanf("%lld",&s[i].v),s[i].id=i;
    int l=0,r=n+1;
    while (l<r)
    {
        int mid=(l+r)>>1;
        if (check(mid)) l=mid+1;
        else r=mid;
    }printf("%d\n",l-1);
    return 0;
}

H Cutting Papers

题目难度：easy

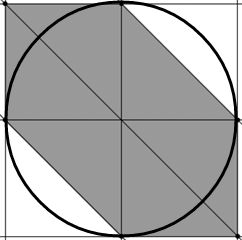
题目大意：给出一个不等式|x|+|y|+|x+y|<=n，问这个不等式构成的封闭区域和以这个封闭区域中心为圆心半径为n/2的圆形的面积并。

赛时经历：

比赛的时候直接用函数图像生成器画出不等式了。。。有点作弊的嫌疑

实际上没必要用函数图像生成器画，直接分四个象限讨论即可

不过这次比赛实在是乱七八糟了，甚至也没有oms，就没管那么多了

参考代码：

查看代码

 #include<iostream>
#include<cstdio>
#include<cmath>
const long double pi=acos(-1.0);
int main()
{
	long double n;scanf("%Lf",&n);
	long double r=n/2;
	printf("%.10Lf\n",2*r*r+pi*r*r/2);
	return 0;
}

F A Stack of CDs

题目难度：easy-medium

题目大意：有一堆圆形，知道从底向上的顺序，上面的圆形会覆盖原来的圆形，问从上往下能看到的部分的周长。

赛时经历：

一开始题意看了4、5遍才看懂，那么就是直接枚举每个圆和上面的圆的交点，转换成圆心角，然后做区间并即可。

需要注意的是要特判当前圆如果被上面的圆包含则break，如果包含上面的圆则continue。

丁老师先写的，不知道为啥会WA，明明都是同一个思路，可能是写假了。

然后我也写了一版，我一开始还以为我的也会有精度误差导致WA，后来觉得这个精度误差没法忽略就直接交了，然后直接A了。

主要思路就是计算圆心角的时候可以通过atan2计算交点的中心点的角度，然后再通过余弦定理求出圆心角的一半，硬做即可。

参考代码：

查看代码

 #include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<algorithm>
#define For(i,a,b) for(int i=a;i<=b;i++)
std::vector<std::pair<long double,long double> > Segment;
const int N=1010;
const long double pi=acos(-1.0);
long double x[N],y[N],r[N];int n;
long double dis2(long double x1,long double y1,long double x2,long double y2)
{
	return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
long double dis(long double x1,long double y1,long double x2,long double y2)
{
	return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main()
{
	scanf("%d",&n);
	For(i,1,n) scanf("%Lf%Lf%Lf",&x[i],&y[i],&r[i]);
	long double ans=0;
	For(i,1,n)
	{
		int flag=1;
		Segment.clear();
		For(j,i+1,n)
		{
			long double len2=dis2(x[i],y[i],x[j],y[j]);
			long double len=dis(x[i],y[i],x[j],y[j]);
			if (len2>=(r[i]+r[j])*(r[i]+r[j])) continue;
			if (len2<=(r[i]-r[j])*(r[i]-r[j])) if (r[i]<=r[j]) {flag=0;break;}else continue;
			long double a=acos((r[i]*r[i]+len2-r[j]*r[j])/(2*r[i]*len));
			long double b=atan2(y[j]-y[i],x[j]-x[i]);
			long double l=b-a;
			long double r=b+a;
			if (l<-pi) Segment.push_back(std::make_pair(l+2*pi,pi)),Segment.push_back(std::make_pair(-pi,r));
			else if (r>pi) Segment.push_back(std::make_pair(l,pi)),Segment.push_back(std::make_pair(-pi,r-2*pi));
			else Segment.push_back(std::make_pair(l,r));
		}
		if (!flag) continue;
		std::sort(Segment.begin(),Segment.end());
		long double st=-pi,ed=-pi,tot=0;
		For(j,0,(int)Segment.size()-1) 
		{
			if (Segment[j].first>ed) 
				tot+=ed-st,st=Segment[j].first,ed=Segment[j].second;
			else
				ed=std::max(ed,Segment[j].second);
		}tot+=ed-st;
		ans+=r[i]*(2*pi-tot);
	}
	printf("%.10Lf\n",ans);
	return 0;
}

D Birds in the tree

题目难度：easy-medium

题目大意：给定n个节点的树，树上每个节点的颜色为0或1，问最终有多少个子联通图的的所有叶子节点（度为1）颜色都是一样的。

赛时经历：

什么智障题意，看了群里的分析才读懂。。。

那就显而易见是树形dp了。

宇彬和我各写了一版，都一发A了，好耶！

我用dp[i][0/1][0/1]表示i作为根节点是否与父亲连颜色为0/1 的合法子图数，然后讨论一下根节点i连几个儿子，它是否作为子图叶子结点即可。

参考代码：

查看代码

 #include<iostream>
#include<cstdio>
#include<vector>
#define For(i,a,b) for(int i=a;i<=b;i++)
const long long mod=1e9+7;
const int N=3e5+1000;
std::vector<int> To[N];
long long dp[N][2][2],ans;
int n;char color[N];
void dfs(int now,int pa)
{
    long long tmp[2],sum[2];tmp[0]=tmp[1]=1;sum[0]=sum[1]=0;
    int now_color=color[now]-'0';
    For(i,0,(int)To[now].size()-1) if (To[now][i]!=pa)
    {
        int v=To[now][i];
        dfs(v,now);
        For(j,0,1) tmp[j]=tmp[j]*(dp[v][1][j]+1)%mod,sum[j]=(sum[j]+dp[v][1][j])%mod;
    }
    dp[now][0][now_color]=tmp[now_color];
    dp[now][0][now_color^1]=(tmp[now_color^1]-sum[now_color^1]+mod-1+mod)%mod;
    dp[now][1][now_color]=tmp[now_color];
    dp[now][1][now_color^1]=(tmp[now_color^1]-1+mod)%mod;
    For(i,0,1) ans=(ans+dp[now][0][i])%mod;
//     printf("?? %d %lld %lld %lld %lld\n",now,dp[now][0][0],dp[now][0][1],dp[now][1][0],dp[now][1][1]);
}
int main()
{
    scanf("%d",&n);
    scanf("%s",color+1);
    For(i,1,n-1) 
    {
        int x,y;scanf("%d%d",&x,&y);
        To[x].push_back(y);
        To[y].push_back(x);
    }
    dfs(1,0);
    printf("%lld\n",ans);
    return 0;
}

A Don't Starve

题目难度：meidum

题目大意：给定N个点有食物（每个食物在人物离开后会刷新，即可重复吃），每个点有一个坐标。

起点是原点，行走的规则是每一步都必须严格短于上一步（第一步任意走），问最优的方案下能够吃到多少次食物。

数据范围：1<=N<=2000

赛时情况：

比赛一开始就看了，结果看不懂，也没说起点在哪，比赛最后改题面了才重新开这题。。。

一开始以为这题是用搜索+剪枝去做，用dp[i][j]表示到达第i个点且吃j个事物的上一步最大距离。

发现一共有n2个状态，每个状态枚举下一步可走的n个点，复杂度n3。。。直接TLE了

比赛的时候我一直往建图然后跑拓扑排序DP找最长路去做，但是即使可以用bitset优化建图到n3/64（从大到小排序边然后保证当前的边的上一步是前面的边，即无后效性），拓扑排序的复杂度还是n3，因为一共有n3条边。。。

比赛倒数五分钟发现没有必要建图，我把边排序以后直接记录从起点到所有点的最大距离max[i]，然后每次把长度相同的所有边加入，用类似分组背包的方式更新最大距离。。。

这样的复杂度是O(n2logn)

结果我在比赛结束后15分钟立刻就把这题A了。。。可惜太晚了

参考代码：

查看代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#define For(i,a,b) for(int i=a;i<=b;i++)
#define Frd(i,a,b) for(int i=a;i>=b;i--)
const int N=2010;
long long x[N],y[N],max[N],temp[N];
struct EDGE
{
	long long len;int u,v;
};std::vector<EDGE> Edge;
int cmp(const EDGE&a,const EDGE&b){return a.len>b.len;}
int main()
{
	int n;scanf("%d",&n);
	For(i,1,n) 
	{
		scanf("%lld%lld",&x[i],&y[i]);
		For(j,1,i-1) Edge.push_back((EDGE){(x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]),i,j});
		Edge.push_back((EDGE){x[i]*x[i]+y[i]*y[i],0,i});
	}
	std::sort(Edge.begin(),Edge.end(),cmp);
	For(i,1,n) max[i]=-0x3f3f3f3f,temp[i]=-0x3f3f3f3f;max[0]=0;temp[0]=0;
	For(i,0,(int)Edge.size()-1)
	{
		int l=i,r=i;while (r+1<Edge.size()&&Edge[r+1].len==Edge[l].len) r++;
		For(j,l,r) 
		{
			if (Edge[j].u) temp[Edge[j].u]=std::max(temp[Edge[j].u],max[Edge[j].v]+1);
			if (Edge[j].v) temp[Edge[j].v]=std::max(temp[Edge[j].v],max[Edge[j].u]+1);
		}
		For(j,l,r) 
		{
			if (Edge[j].u) max[Edge[j].u]=temp[Edge[j].u];
			if (Edge[j].v) max[Edge[j].v]=temp[Edge[j].v];
//			printf("??%lld %d %d %lld %lld\n",Edge[j].len,Edge[j].u,Edge[j].v,max[Edge[j].u],max[Edge[j].v]);
		}
		i=r;
	}
	long long ans=0;For(i,1,n) ans=std::max(ans,max[i]);
	printf("%lld\n",ans);
	return 0;
}

G KFC Crazy Thursday

题目难度：medium

题目大意：以字母k/f/c/结尾的回文子串计数

数据范围：1<=|S|<=5e5

解题思路：

1、枚举回文子串中心点，二分回文子串最大长度+字符串哈希

2、回文自动机版题

回文自动机有空得补一下。

posted @ 2022-08-02 11:31 th-is 阅读(52) 评论(0) 收藏举报

刷新页面返回顶部

th-is

"蔚来杯"2022牛客暑期多校训练营5

K Headphones

C Headphones

B Watches

H Cutting Papers

F A Stack of CDs

D Birds in the tree

A Don't Starve

G KFC Crazy Thursday

公告