数据结构01—绪论作业

一.作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。
有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3

二、博客作业内容

1.作业内容

用ADT的抽象数据模型描述你的有理数数据类型。
ADT Rational {

数据对象：D={e1,e2|e1,e2属于整数类型}

数据关系：R={<e1,e2>|e1为有理数分子，e2为有理数分母}

基本操作：

CreateRational（&t，e1，e2）//操作结果：构造有理数t，e1为有理数分子，e2为有理数分母

DestroyRational（&t）//操作结果：销毁有理数t

Get（t,i,&e）//操作结果：用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母

Put（&t,i,e）//操作结果：将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母

Add（t1,t2,&t3）//操作结果：有理数T1,T2相加,结果存入有理数T3

Substract（t1,t2,&t3）//操作结果：有理数T1,T2相减,结果存入有理数T3

Multiply（t1,t2,&t3）//操作结果：有理数T1,T2相乘,结果存入有理数T3

Divide（t1,t2,&t3）//操作结果：有理数T1,T2相除,结果存入有理数T3

2.数据结构、函数说明

1、头文件

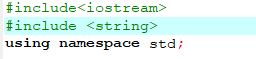
2、函数

int gys(int x,int y)    /*定义求最大公约数函数*/

int gbs(int x,int y)    /*定义求最小公倍数函数*/

void yuefen(int fz,int fm)          /*定义约分函数*/

void add(int a,int b,int c,int d)       /*定义加法函数*/

void sub(int a,int b,int c,int d)   /*定义减法函数*/

void mul(int a,int b,int c,int d)       /*定义乘法函数*/

void div(int a,int b,int c,int d)   /*定义除法函数*/

 3、代码实现

1、加法

void add(int a,int b,int c,int d) /*定义加法函数*/
{
int u1,u2,v=gbs(b,d),fz1,fm1;
u1=v/b*a;
u2=v/d*c;
fz1=u1+u2;
fm1=v;
yuefen(fz1,fm1);
}

2、减法

void sub(int a,int b,int c,int d) /*定义减法函数*/
{
int u1,u2,v=gbs(b,d),fz1,fm1;
u1=v/b*a;
u2=v/d*c;
fz1=u1-u2;
fm1=v;
yuefen(fz1,fm1);
}

3、乘法

void mul(int a,int b,int c,int d) /*定义乘法函数*/
{
int u1,u2;
u1=a*c;
u2=b*d;
yuefen(u1,u2);
}

4、除法

void div(int a,int b,int c,int d) /*定义除法函数*/
{
int u1,u2;
u1=a*d;
u2=b*c;
yuefen(u1,u2);
}

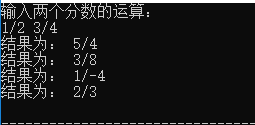
3、结果展示

1、

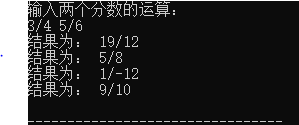
2、

5、总结

数据结构是计算机存储、组织数据的方式。个人以为要想学好数据结构要有深刻的做题体会与心得，掌握好的算法，但是对于这道题我并没有思路，所以没有很好的完成。精心选择的算法对于解题至关重要。