评价类-2.TOPSIS法（优劣解距离法）

      同样是评价类模型，先拉踩一下之前的层次分析法（弊端）

            1.评价的决策层（n）不能太多 2.如果决策中指标数据是已知的，使用更加准确的方法

      由此引出TOPSIS法：

      两种指标：极大型指标（效益型指标）越大越好，如：成绩、分数等

                        极小性指标（成本型指标）越小越好，如：成本等

      然而有两种指标并不方便比较与计算，故将进行指标正向化，也就是将极小型指标转化为极大型指标的方法。

                                                                            公式：max-x

      而为了消去不同指标量纲的影响，需要对正向化后的矩阵进行标准化处理：、

                                                                   

 

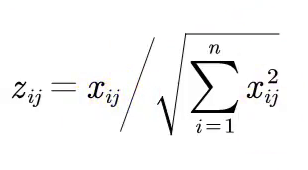
      假设有n个要评价的对象，m个评价指标，计算评分时：z与最大值的距离/（z与最大值的距离+z与最小值的距离）

      最后对评分进行归一化

      补充其他两种指标：中间型指标（靠近某个值）区间性指标（落在某个区间）

第一步：将原始矩阵正向化

      极小→极大：可以使用上面提到的max-x，也可以在元素全部为正数时使用1/x。

 

      中间→极大：x'=1-|x-xbest|/M（M=max【|x-xbest|】）

      区间→极大： M={a-min,max-b}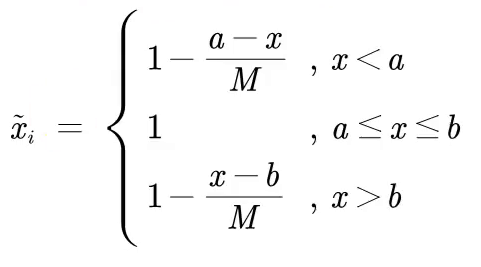                 

第二步：正向化矩阵标准化

第三步：标准化矩阵归一化