【竞赛】CMC备赛

大纲

级数

敛散性判断【比较判别法、比值判别法、根值判别法、积分判别法（注意，到这里的都是正项级数的判别法）、莱布尼茨判别法、阿贝尔判别法、迪利克雷判别法】、幂级数、傅里叶级数

幂级数的收敛半径、收敛区间、收敛域、和函数、阿贝尔引理

傅里叶级数：周期为\(2\pi\)的，迪利克雷定理，周期为2l的

微分方程

一阶微分方程：变量可分离的（注意奇解）、齐次方程、一阶线性方程、伯努利方程、全微分方程

可降阶的二阶微分方程

线性微分方程：二阶线性微分方程、二阶常系数线性齐次微分方程、二阶常系数线性非齐次微分方程、欧拉方程

向量代数与空间解析几何

叉乘混合积

空间中的平面和直线：平面一般式截距式三点式，直线点向式两点式一般式参数式
距离和角度的各种计算

空间中的曲面和曲线：空间曲面旋转曲面常见二次曲面法线切平面，空间曲线切线法平面

多元微分学

积分

那些典

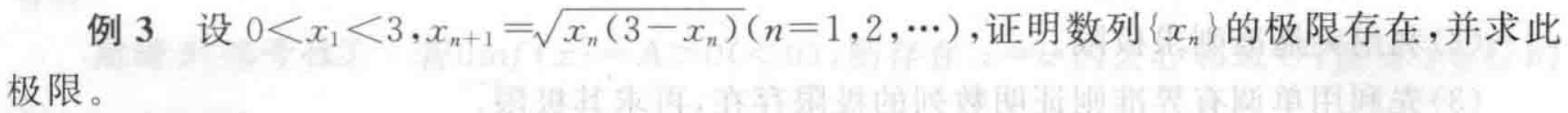
回忆：证单调有界是证存在极限的常用方法。

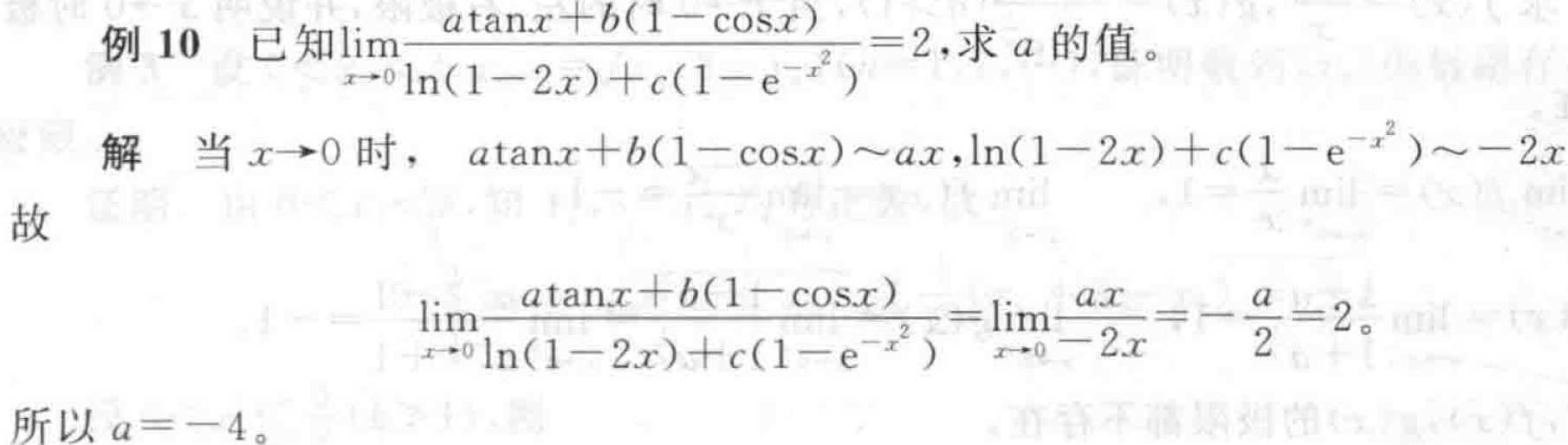
虽然是按等价无穷小的方法写的但是明显用泰勒展开去想就行了。

简单但很好的考察了连续性。

简单但容易晕，看清谁是谁的函数。

难点。

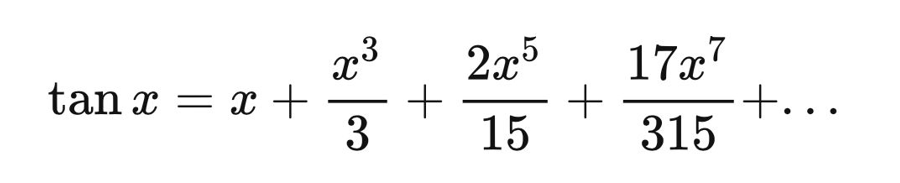
记住第二项。这个和伯努利数有关系。

回顾一下隐函数吧！

微分方程：一阶、可降次二阶、线性微分方程

灵活！

回顾！

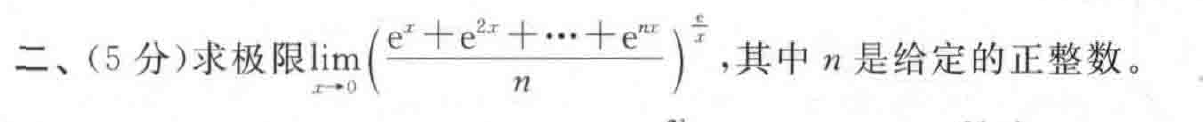
等价无穷小替换条件警告！

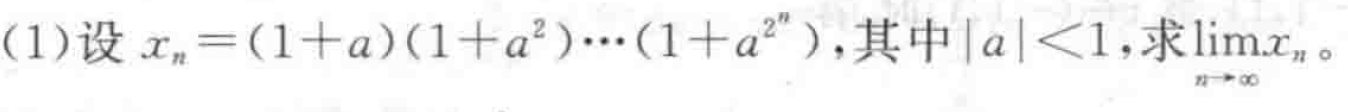
做一次就会的变形罢了。

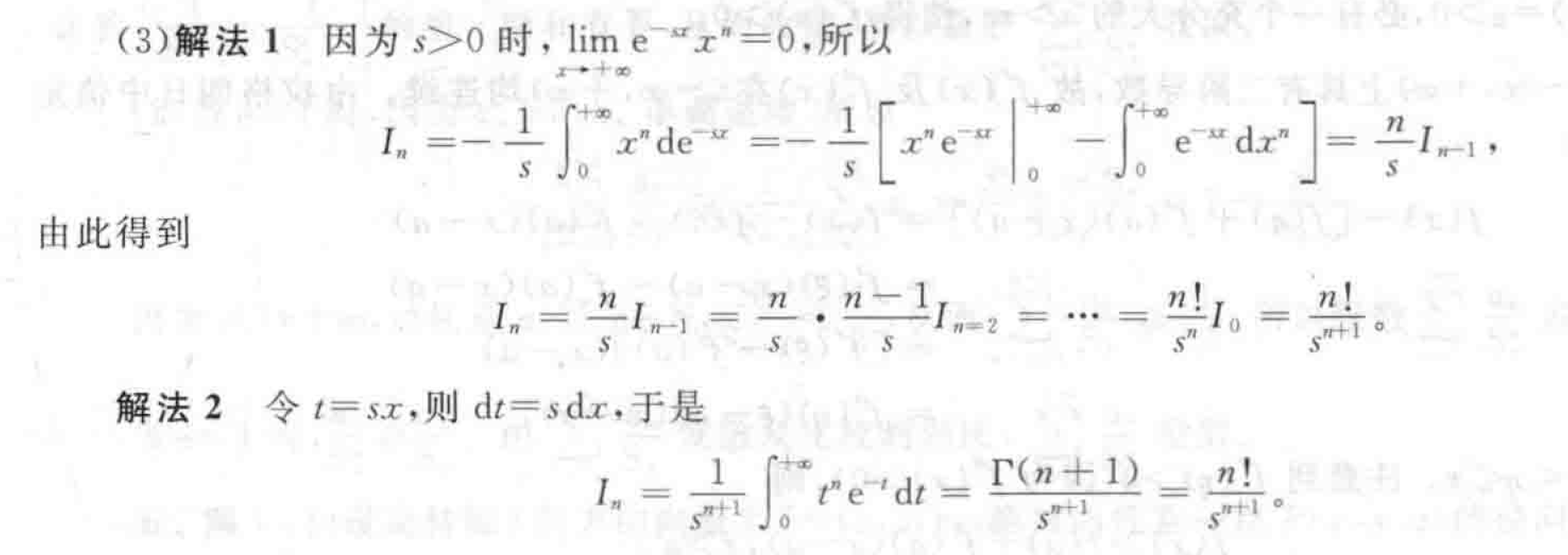
两个方法都要熟悉。回顾\(\Gamma\)函数。

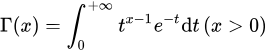
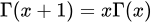
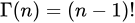
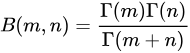
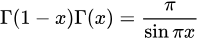
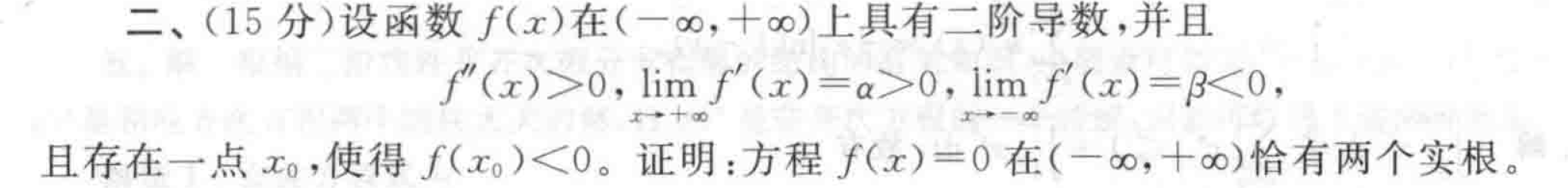
有两个根好证。用罗尔定理反证恰有两个根还是挺妙的。

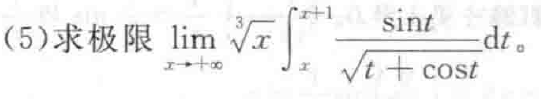
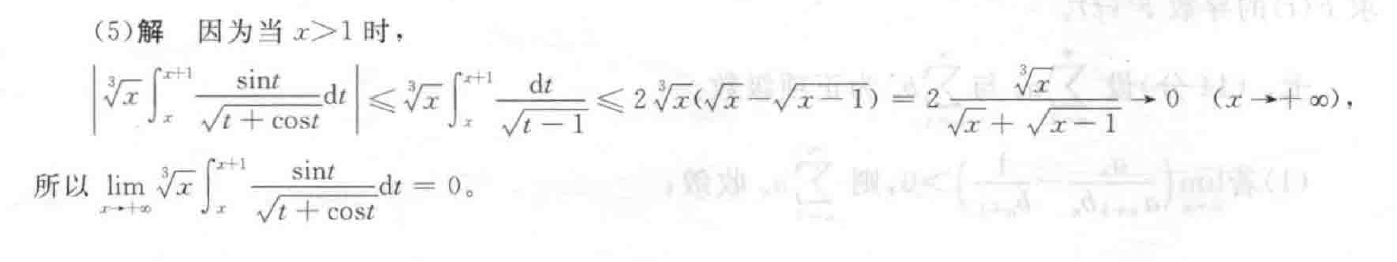
好狠的放缩。。。

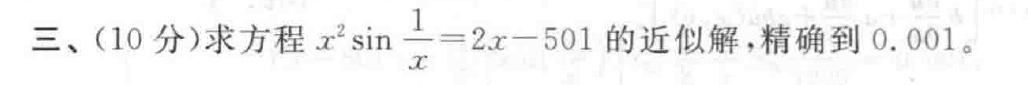
学到一招。好久没用过这个形式的泰勒展开了。答案倒是好猜的。

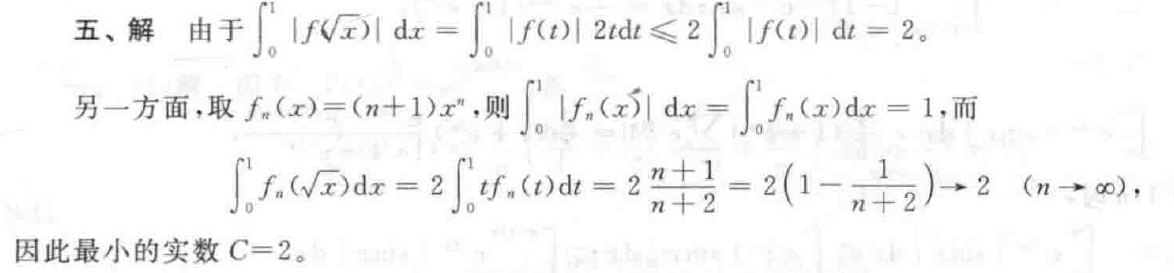
两道都是好题、典题。

一些常用数学工具

1. 级数收敛判别法

正项级数部分和有界
阿贝尔判别法

狄利克雷判别法

2. stolz定理

冲刺！

隐函数求导躲不掉的一道题