离散数学——期中经典题型

贝叶斯定理；概率、方差、期望之间的关系; 期望的线性性质

两道题都用到了期望的线性性质。

第三问很有意思，高三数学竞赛见过类似的技巧。

鸽笼原理

关键是学会构造抽屉！

证明关系的某些性质

关于格的定义要清楚，用来解决1,3两问。这个题的第二问略有难度，要知道有界格是一定有上下确界的！

好题！第一问反证找矛盾，第二问取一特殊情况即可，实际上还是在考察偏序、格、全序的定义。

也是好题！只要你理解了，出现等价关系，必有等价类划分，那么这个题就做出来了。当然，用数学语言描述还是略有难度的。举个例子，\(A=\{1,2,3,4,5\},R=\{(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)\},A/R=\{[1],[4],[5]\},\)其中\([1]=\{1,2,3\},[4]=\{4\},[5]=\{5\}.\)那我只需要让\(f(x)=[1](x=1,2,3),f(4)=[4],f(5)=[5]\)

下面这个题还是挺难的。还好有提示，瞬间变成水题——一方面\(\wedge A\in A\)所以\(f(\wedge A)\preccurlyeq \wedge A\)
另一方面\(f(\wedge A)\preccurlyeq A\)中任意元素，所以\(f(\wedge A)\)是\(A\)的下界，所以$\wedge A\preccurlyeq f(\wedge A) $

而且还容易证明这个不动点是最小的。若\(f(p)=p\),则\(p\in A\),则\(p\leq \wedge A\)

相当水的一道题，只需证明\(R^2=R\).不过我们需要注意一个性质，R传递当且仅当\(R^2\subseteq R\).

这是道简单的好题：

令R为A上的一个关系。试证明：R是一个等价关系当且仅当
存在一个集合B及一个函数f:A→B使得xRy⟺f(x)=f(y).

数学归纳法证明

结构归纳法证明归纳定义的集合具有某些性质：

这题不用归纳也行，但是归纳说起来更清楚些。这题也是证明函数性质的经典题目。

这个归纳很灵活~10个奠基

归纳法+极端原理，老师课上讲的，很简单但很有代表性

命题逻辑，自然演绎法

学会几个词：前提引入，全称示例，全称生成，存在示例，存在生成。化简律，德摩根律，拒取式（也叫否定后件），析取三段论，假言三段论，假言推理，assumption，。
更专业的：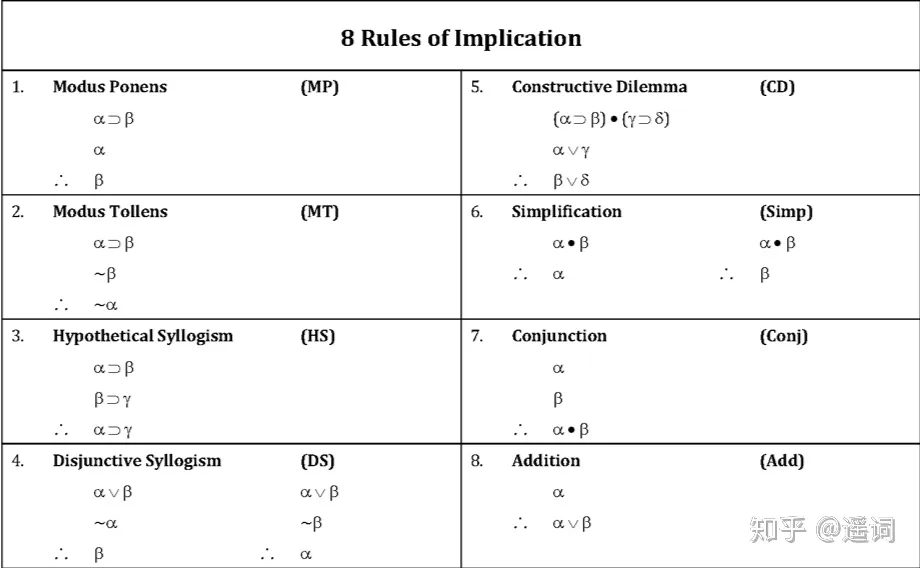

函数的性质，判断集合基数

这类题普遍较难，要重点关注！
如何构造函数？
双射太难，能不能用两个函数去证？


下面这个题看似不起眼，实际上考察了你对f(X)(X是一个集合)的理解。

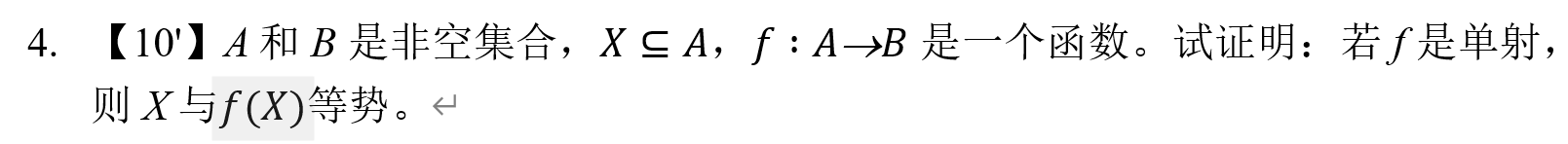
数论

费马数的定义。费马数的性质：两两互质。

梅森素数的定义(\(2^{p}-1\) 为素数, \(p\)也为素数)

初学数论，对这题有印象。

其他

考察概念和计数的基本功

区分：反对称，非对称，反自反，反传递。

区分：等价关系，偏序关系，拟序关系（反自反+传递），相容关系（自反+对称）

区分闭包：r,s,t
只有s和r不能交换复合顺序，\(s(t(R))\subseteq t(s(R))\)
其他复合方式顺序交换都不影响结果

区分：良序，全序，良基

区分：格，分配格，有界格，完全格...
由“简单”的归纳（对子集中元素个数归纳）可知，若偏序格\(<L,\preccurlyeq>\)中L是有限集，则这个格一定是完全格。
完全格一定是有界格。有界格不一定是完全格。
有限格一定完全+一定有界。。。总之就是有限格 强于 完全格 强于 有界格。

折线法，卡特兰数

去年新鲜出炉的题目
注意读题，是画n=4的哈斯图不是n=3的。这个哈斯图还是很有意思很对称的。
第三问我想的是证明a|b，a&b分别是最小上界和最大下界，但答案让我吃惊——因为全0和全1是整个偏序集的下/上界，利用确界原理即可。。。

下面这题，同构应该是抽象代数的范畴了。在这里我们只需记住怎么证明两个偏序集同构：找一个合适的\(f\).暂时不需要了解这方面的具体知识。

---

宿舍长提出的问题的解决：