【课业】离散系统整理复习【已完结】
题型划分(根据往年期末卷)
集合基数/函数性质
哈密顿图与欧拉图
连通图
集合的关系的性质
数论
群论
生成树相关算法、性质
概率论(期望相关?贝叶斯定理?)
逻辑
组合计数
匹配
布尔代数基础
...
图论
先来复习重要又有难度但我还没忘光的东西罢了。。。
连通度
割点的概念。
\(v\)是割点当且仅当存在\(V-\{v\}\)的分划\({V_1, V_2}\), 使\(\forall u∈V_1, w∈V_2, uw-\)通路均包含\(v\)。
删一条边最多增加一个连通分支。
割边的概念。
e是割边当且仅当e不在G的任一简单回路上,当且仅当存在\(V-\{v\}\)的分划\({V_1, V_2}\), 使\(\forall u∈V_1, w∈V_2, uw-\)通路均包含\(e\)。
点连通度与边连通度的概念,k连通与k边连通的概念。
\(\kappa(G)\leq\lambda(G)\leq\delta(G)\)及其证明。

一个更像例题的定理:
2-连通图也叫块。


边版本的Witney:

还可以推广!

作业中和此相关的题目


有向图里的连通概念
弱连通、单连通、强连通


归纳证明很容易。

什么样的无向图可以通过给边定向变成强连通图?显然要2边连通,这事实上是充要的,以下的算法同时也是充分性的证明。
输入:无环2-边连通无向图G (设VG={v1,v2,…,vn})
输出:以G为底图的强连通有向图

当最小度、边数足够大的时候证明连通:



最短通路问题
Dijkstra算法、Floyd-Warshall算法、最短旅行商问题
跟着算法步骤走一遍~
欧拉图
 (1)(2)都由归纳易证。
(1)(2)都由归纳易证。

对于有向图:若G是弱连通的有向图,则G中存在有向欧拉回路的等价条件是G中任一顶点的入度等于出度。
构造欧拉回路:Fleury算法
欧拉图G是以v为始点的随机欧拉图当且仅当 G中任一回路均包含v。
哈密顿图
其中, \(P(G-S)\)表示图\(G-S\)的连通分支数.
理由:设\(C\)是\(G\)中的\(Hamilton\)回路, \(P(G-S)\leq P(C-S)\leq|S|\)
向一个图中顶点之间加边不会增加连通分支。
充分条件:
只证Ore定理:反证,不妨设G是边极大非哈密顿图
怎么进而推出通路版本:
Ore定理的应用:非常经典的一道题!(不用归纳更简单!)

下面这张图体现了立方体图、哈密顿图、格雷码、二进制位串、二部图完美匹配之间的关系。两个图秒懂。


对于任意n,\(Q_n\) 均为存在完美匹配的二部图。注意边的两个顶点只有一位不同。对每个顶点二进制编码,根据编码中1 的个数的奇偶性可将
顶点分为两部分。对所有编码为\(a_0a_1a_2...a_{n−1}0\) 的顶点,将其匹配到\(a_0a_1a_2...a_{n−1}1\),即可得到完美匹配。
至于哈密顿回路在哪里?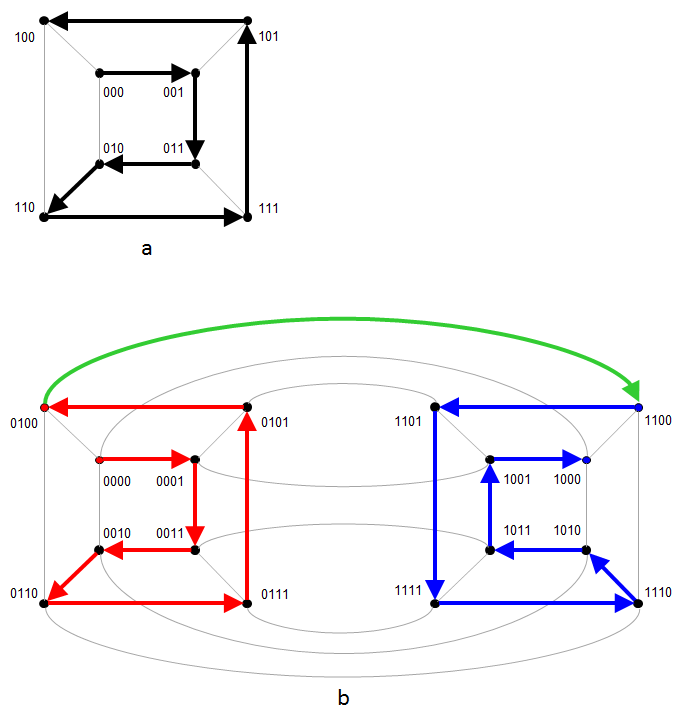
归纳构造简单的很。
下面是个哈密顿图的典型应用:

完全二部图存在哈密顿圈当且仅当两个部的顶点数相等,这在一些组合问题中也有应用。
竞赛图相关
竞赛图:底图为完全图的有向图(无双向边)
这里有一个经典证明,证明竞赛图是哈密顿图当且仅当它是强连通图。必要性显然。充分性:
还有一道真题,也是很重要的结论
每个竞赛图均包含一条有向哈密顿通路
根树
定义:底图为树的有向图称为有向树。
定义:若有向树恰含一个入度为0的顶点,其它顶点入度均为1,则该有向树称为根树,那个入度为0的顶点称为根。
m元树:每个内点至多有m个子女。2元树也称为二叉树
完全m元树(full m-ary tree):每个内点恰好有m个子女
平衡:树叶都在h层或(h-1)层, h为树高。
有序:同层中每个顶点排定次序。有序二叉树通常也简称为二叉树
关于完全m元树,利用算两次的思想容易求出内点进而求出树叶的个数
有序根树的遍历:前序中序后序
前/后缀表示法
二叉搜索树
决策树
最优二叉树、霍夫曼编码
生成树
DFS、BFS
求最小生成树:Prim算法,Kruskal算法
二部图、匹配


推论1:

推论2:

Berge定理

一道超经典题,必须得记住——替换法。
令G 为一无向带权连通图,假设图中存在一个回路. 试证明:在此回路上若存在一条边e 其权值严格大于此回
路上的其它各边,则e 不在G 的任何最小生成树中。

代数系统&群论
代数系统

子群
发现自己真的连这个都忘了。。

元素生成的子群、循环群
关于群最基本的定理
 (其实生成元和可逆元是一回事。)
(其实生成元和可逆元是一回事。)
 (好题)
(好题)
中心
陪集、代表元


正规子群当然还有别的定义
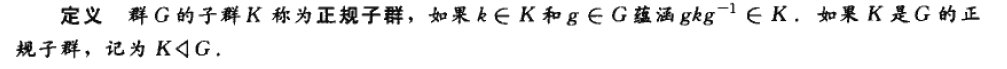

很重要的拉格朗日定理








置换群

全体置换及乘法运算构成对称群,偶置换及其乘法运算构成交错群。
凯莱定理



群的直积
群同态基本定理




该定理表明,若 N 是群 G 的正规子群,则商群 G/N 是群 G 在自然同态下的像(Imπ),并且正规子群是自然同态的核。

容易理解的手写笔记


关系
关系的基本性质
关系是有序对的集合,关系可以用矩阵、图表示
关系的复合的矩阵算法:\(M_{f\circ g} = M_gM_f\)
反对称:不能出现双向边 非对称:不能出现双向边和自环 反自反:不出现自环 反传递
等价关系、等价类、划分


偏序
自反,反对称,传递。
概念:可比,全序,良序,良基,字典序,哈塞图,覆盖(偏序集是它的覆盖关系的传递闭包的自反闭包),极大元,极小元,最大元,最小元,上确界,下确界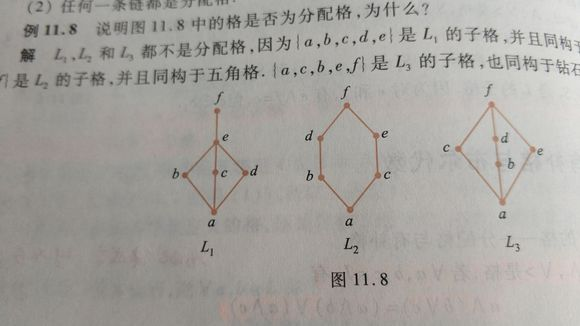
格,相容,拓扑排序


这图真不错!Misky:高度为t则可划分为t条反链
对偶的Dilworth:宽度为t则可划分为t条链。
利用Dilworth可以轻松推出Erdos-Szekeres定理:mn+1个元素必有m+1链或n+1反链
当然还有之前学过的证明方法

数论

概率论
记几个公式就够了
贝叶斯公式
布尔代数

原子的概念
表示定理
2的幂

这个就得当定理记住~证明完备性别忘了1和0的表示,不具备完备性也用0去证,NOR可以完备
可爱的真题们

乍一看有点懵——关系怎么还有同构一说,别和代数系统那里搞混了。

这个就应该当作定理记住。。。尤其是那个上确界。我们之前只知道子群的交一定是子群,但并通常不是子群。
证明确界那里别想复杂,就是很显然~

属实好题,Klein四元群的经典应用

虽然是很好理解但是写清楚还是不容易的。我发现还是把操作方式写出来比较好。从9到0依次插位置。

真是好题,一点都不难为你但是又完美地考察了偏序格的知识

博弈经典题,原试卷答案依托,这个是网上找的。哎呀计科的离散卷子出的水平真不错。

犹豫了半天德摩根律能不能用,然后发现答案直接用啦~

又一道爵士好题!!!不想说啥了已经。

大水题,但也得记住全序咋证。

同样是大水题,但还挺重要的,较好的考察了树的点边关系、握手定理。如果考根树会不会更难?
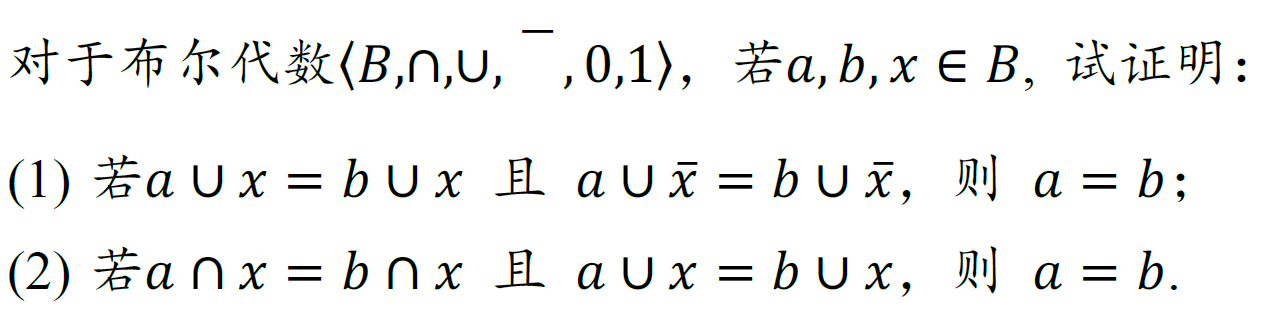
你别说,看着水,如果不练说不定还真能卡你十分钟。。。


友谊图相关。。。图二是证明不相邻顶点的度数相等

最难的一道之一。搞清楚最小上界最大上界的判定。如果一个子集的下界在这个子集里那它当然是最大下界。


经典,期中考前练了好多次。

循环群的子群性质的特殊情况的证明,用带余除法证明必要性

好无聊的题目,没活硬整,虽然作为一个探究/拓展话题是好的。这里要记住同构的判定的写法,即存在点集间双射使得原图中那两个顶点相邻当且仅当对应到同构图中的两个顶点相邻。

作业中出现过,一定得会啊

这不是一眼匹配。。。


最重要的一道,记住黄色部分即可

你别说,软院这题挺好。考察了闭包的定义。

离散也有这个题。挺好。
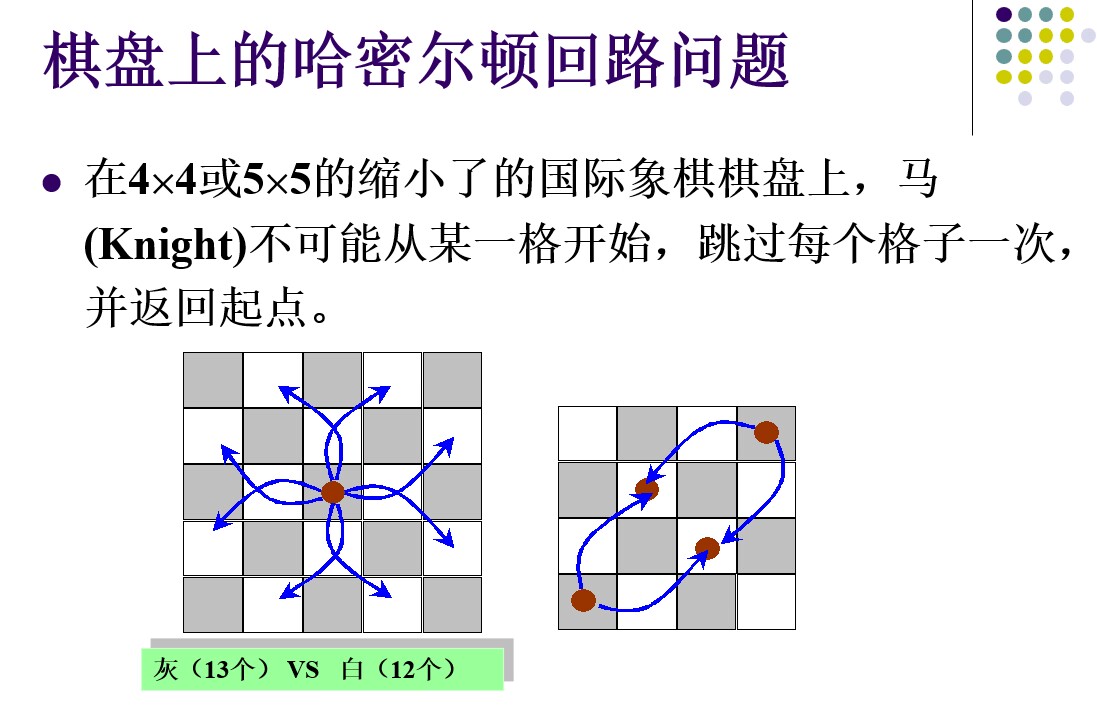
这是lc问的那个版本

我去,生成函数,高级货,不愧是软院2333
网上发现的好题们
 真是绝世好题!法一中,两个不同的集合对称差一定非空;由于叶子所在的边一定在完美匹配中,因此对称差中一定没有叶子。
真是绝世好题!法一中,两个不同的集合对称差一定非空;由于叶子所在的边一定在完美匹配中,因此对称差中一定没有叶子。
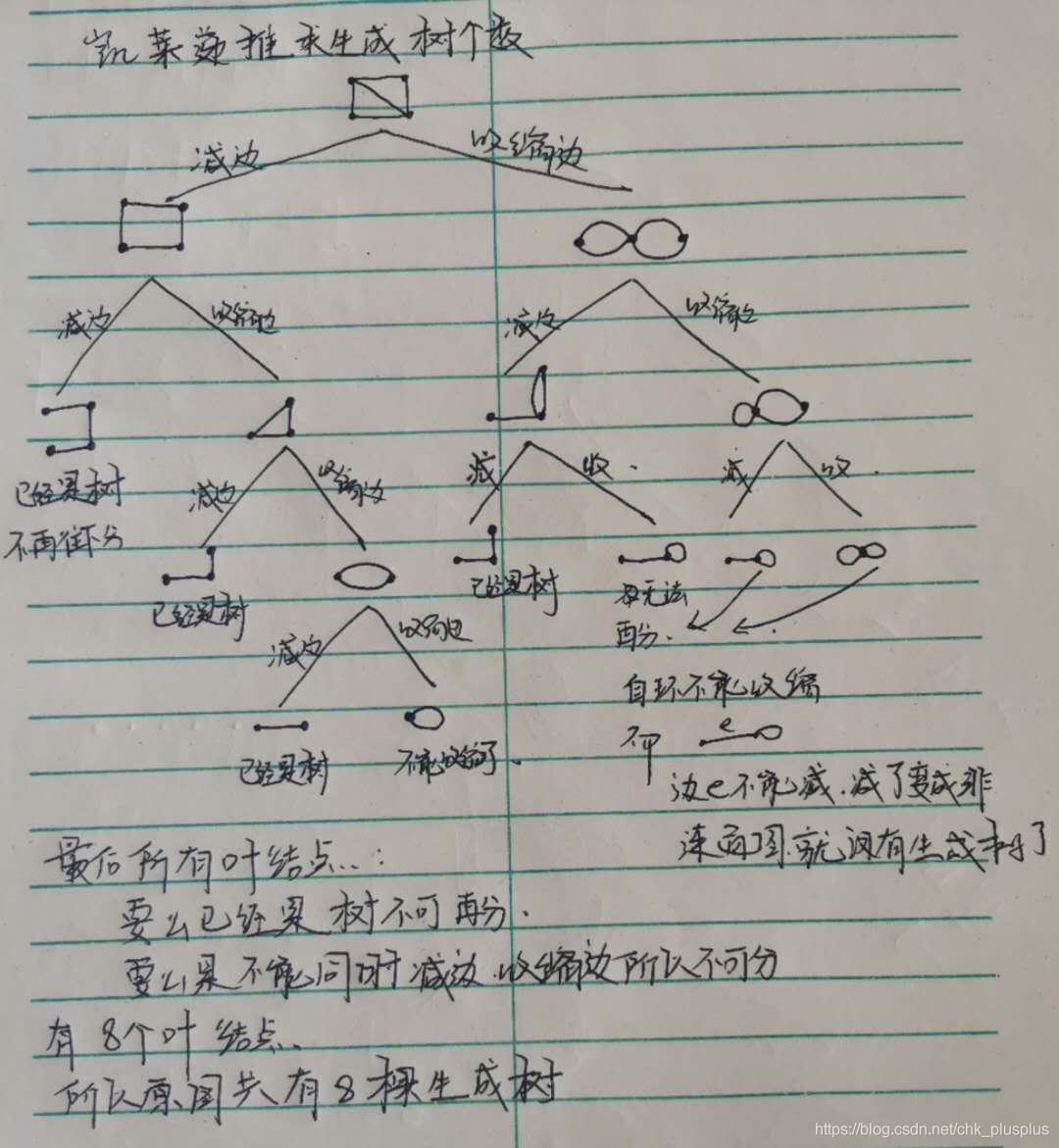
(来自https://blog.csdn.net/chk_plusplus/article/details/105386655)
凯莱定理,其证明是容易的。

这个叫凯莱公式,高中竞赛就见过了

好题!二部图——会算边!

好题~本质上还是在考握手定理,倒腾边点度

白天有人问为什么最小度大于等于2就有圈,解释完就看到这里有个推广~其实还是一回事

这不是有关树理论的最基本的东西吗——别急,后面还有难的
好好好
算法正确性证明
经过隔壁dwz院长的提醒,来专门复习一下各算法,虽然我不是很信他会考
-
Prim算法-替换法


-
Kruskal算法-替换引理法


-
Dijkstra算法-归纳法


-
Floyd-Warshall算法
这个基本步骤好像之前都没提过。。就是每一轮完整更新一遍矩阵,每个数看它所在的行与列对应相加有没有比这个数更小。
-
Warshall传递闭包算法
理解就行。 -
Fleury算法
一些拓展~
斯特林数
折线法



 浙公网安备 33010602011771号
浙公网安备 33010602011771号