刷题记录-剑指offer43：1-n整数中1出现的次数

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

 

最简单的思路是通过和10取余数来拿到每一位的数字，从0遍历到n复杂度是o(n),每个数字取余是o(logn),总的复杂度是o(nlogn),这个复杂度太大

下面这种方法的复杂度只有o(logn):

从个位开始，把输入分成两部分，例如n=3141592

 

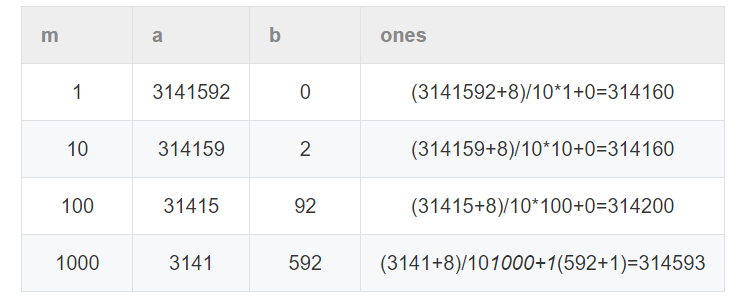
当m=1，意思是个位固定为1，前边为000000-314159的全排列，一共314160

当m=10，十位固定为1，前边为00000-31415的全排列，后边是0-9，一共31416*10=314160

当m=100，百位为1，前边为0000-3141，后面是0-99，一共3142*100=314200

注意，m=1000的时候不能这么算，因为千位上本来就是1，那后边就不能是0-999，否则会出现3141999这种超过n的情况，n要分成0-3139999和3140000-3141592的情况，前者的计算方式可以和原来一样是314*1000，后者中3140000-3140999都不在讨论范围（因为只关心千位为1的个数），3141000-3141592一共593种，所以最后结果为314000+596=314596

一次类推

代码如下，a+8的巧妙之处在于当a的最后一位(当前分析位)为0或1时，加8不产生进位，这是为等于1的情况做准备，而当前分析位为2~9时，不需要考虑特殊情况，所以允许加8产生的进位。

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        if(n<0)
            return 0;
        int cnt = 0;
        for(int i = 1;i<=n;i*=10){
            int a = n/i;
            int b = n%i;
            cnt += (a+8)/10*i+((a%10==1)?b+1:0);  // 注意这里不能写成(a%10<=1),因为某一位为零的话，后边也不能加，例如n=3140592，千位上不允许=1，所以不能加593
        
        return cnt;
    }
}

 更新：

上边的代码有缺陷，输入是1410065408时，i等于10000000000时才能结束循环，但是这个是超过了int的范围，溢出后的 i 正好是1410065408，从而产生错误结果，正确的做法是：https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof/solution/mian-shi-ti-43-1n-zheng-shu-zhong-1-chu-xian-de-2/