用位运算实现加减乘除(3)

用位运算实现加减乘除(2) 中的div方法要求a和b都能转成正数，但是：

系统最小值没法转成绝对值：Integer.MIN_VALUE

所有整数中只有这个数，是转不出绝对值的。

int a = Integer.MIN_VALUE;

System.out.println(-a);

 

所以分4钟情况讨论：

 

重点解析第3中情况：

假设-10就是系统最小，9是系统最大。我们没法把-10/2 转成 10/2，因为系统没有正10，系统最大值只到9.

那怎么算-10/2呢？

-10 先加1 得到-9，将-9/2得到-4。将-2*4 = -8，将-8和-10去比差了多少。-10 - (-8) = -2，差了-2。再将-2/2 = -1，加上原来的-4，得到-5.

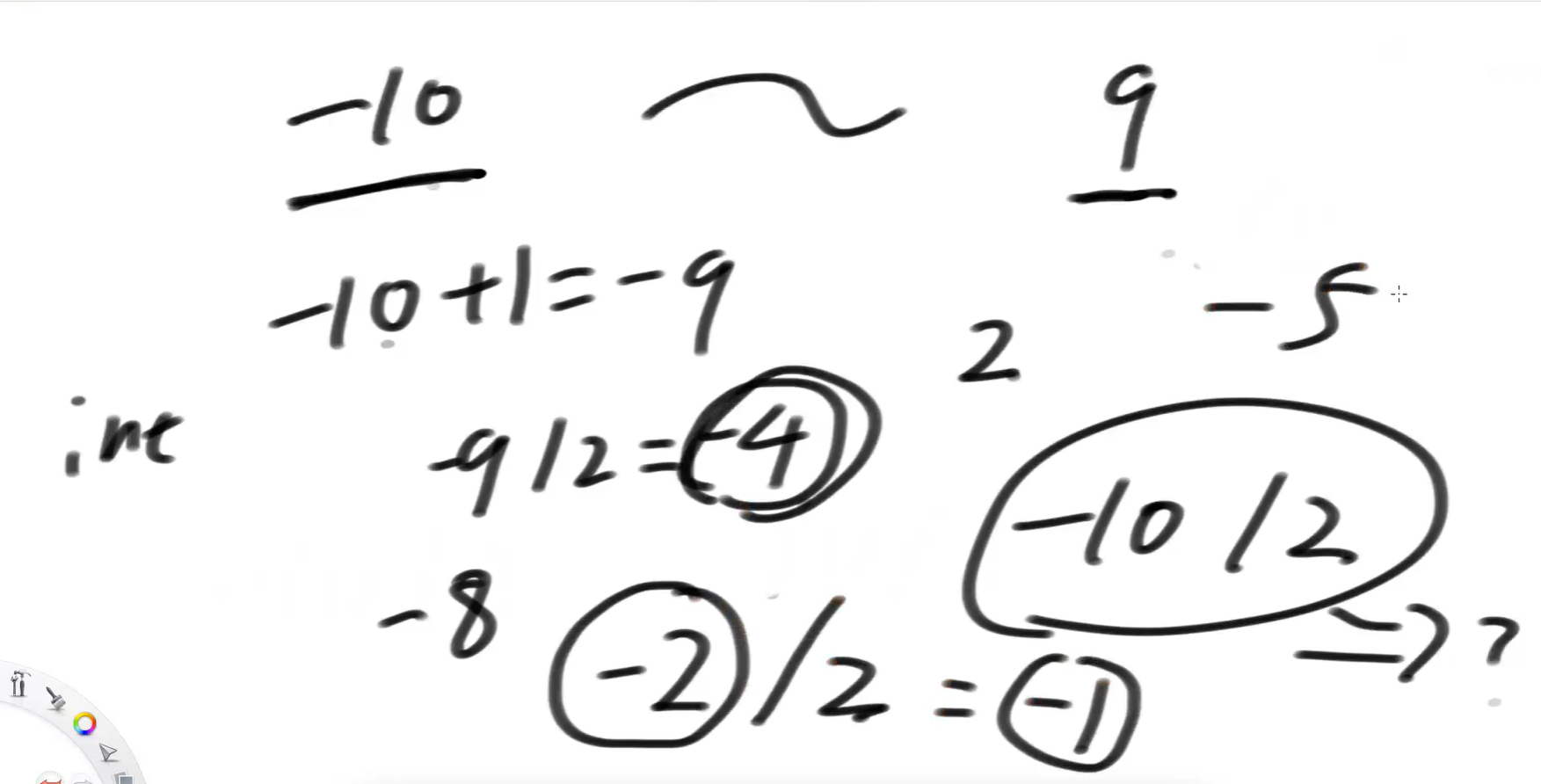
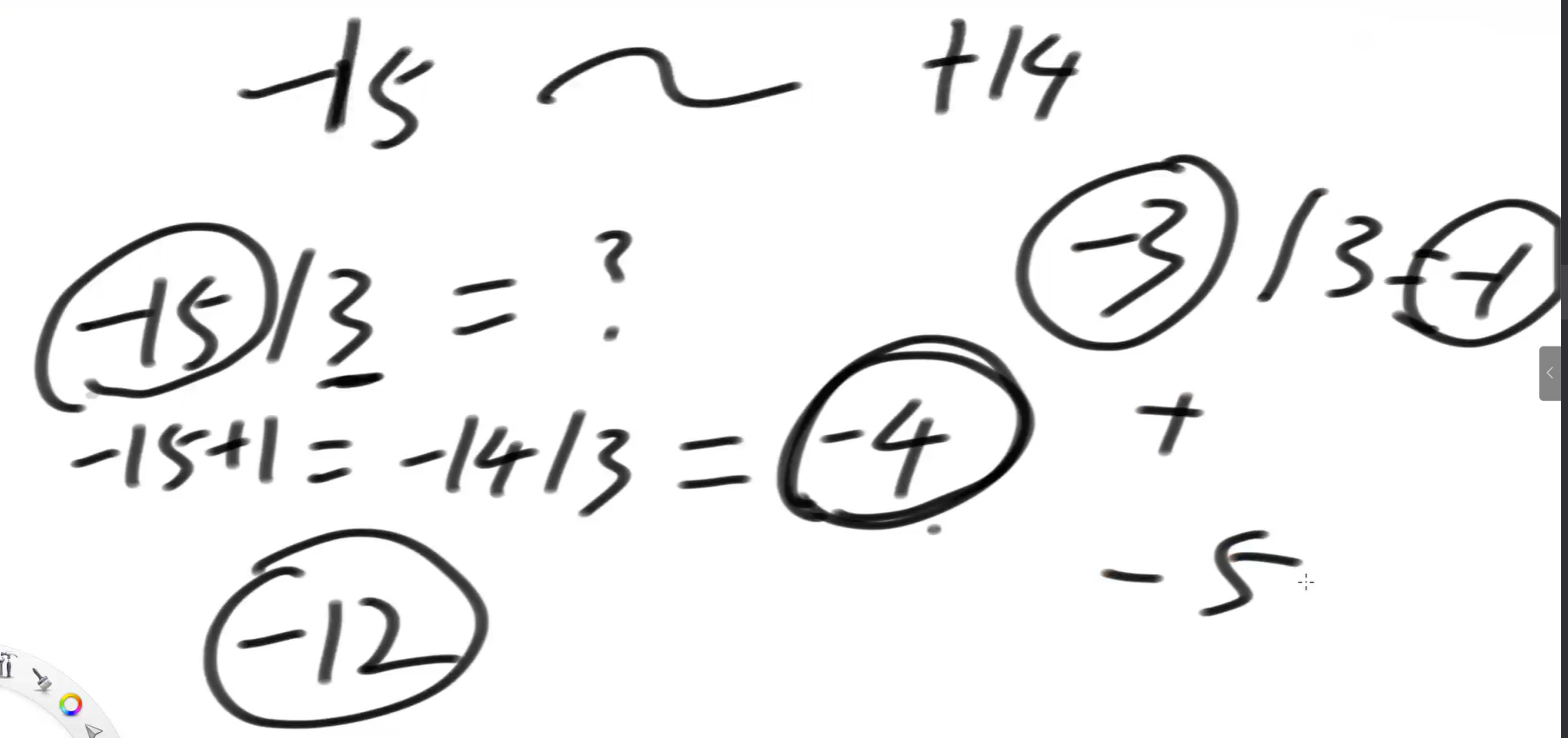
其实很好理解：-4*3 + (-x) * 3 = -15

x = (15 - 4*3）/ 3

x = 1

所以就是-4 + -1 = -5

 

 

代码实现：

package com.cy.class05;

/**
 * 位运算实现+-*\\/
 * 测试连接：https://leetcode.com/problems/divide-two-integers
 */
public class Code03_BitAddMinusMultiDiv {

    public static int add(int a, int b) {
        int sum = a;
        while(b != 0) {
            sum = a ^ b;            //无进位相加信息   ->  sum
            b = (a & b) << 1;       //进位信息  -> b   ->  b'
            a = sum;                //无进位相加信息a  ->  a'
        }
        return sum;
    }

    /**
     * 返回n的相反数
     * 相反数 = 取反 + 1
     * -n = ~n + 1
     */
    public static int negNum(int n) {
        return add(~n, 1);
    }

    public static int minus(int a, int b){
        return add(a, negNum(b));
    }

    /**
     * 乘法
     *
     * 右移：
     * b >> 1，表示右移1，最高位拿符号位来补。
     * b >>>1, 表示右移1，最高位一律拿0来补。
     *
     * 支持负数，道理不好解释，负数的情况下到底发生了什么，跟补码有关，你只要知道同样这套方法既支持正数也支持负数。
     */
    public static int multi(int a, int b) {
        int res = 0;
        while(b != 0) {
            if ((b & 1) != 0) {
                res = add(res, a);
            }
            a <<= 1;
            b >>>= 1;
        }
        return res;
    }

    public static boolean isNeg(int n) {
        return n < 0;
    }

    /**
     * 除法
     *
     * 这个方法在正式开始之前，a和b一定要都转成正数
     *
     * x是非负的，第32位是符号位，肯定是0，所以没必要右移31位。所以for循环i从30开始。
     *
     * 这里^的运算是：非短路逻辑异或，两边的表达式都会执行
     * boolean a = true, b = false;
     * boolean c = a ^ b; // true（不同时为 true/false）
     * 如果需要逻辑异或（对布尔没必要值），直接用 != 更直观： boolean xor = (a != b); // 等效于 a ^ b
     *
     * a ^ b: a和b不同返回true，否则返回false
     *
     * 这个除法必须要求x和y转成正数的形式。
     * 这个方法一定是要能把a和b转成正数才能继续算，但系统最小值没办法转绝对值，所以有局限。
     */
    public static int div(int a, int b) {
        int x = isNeg(a) ? negNum(a) : a;
        int y = isNeg(b) ? negNum(b) : b;
        int res = 0;
        // x / y
        for (int i=30; i>=0; i = minus(i, 1)) {
            if ((x >> i) >= y) {
                res |= (1 << i);
                x = minus(x, y << i);
            }
        }
        //如果a和b符号不一样，取个负号返回；如果a和b负号一样，直接返回答案
        return isNeg(a) ^ isNeg(b) ? negNum(res) : res;
    }

    /**
     * 如果a和b都为系统最小，a = b，返回1
     * 如果b是系统最小，a不是，a / b，因为a的绝对值比b小，一除，向下取整，为0
     * 如果a是系统最小，b不是，将ans = (a + 1) / b，再(a - ans * b) / b 得到结果，再加ans。详细推演过程看草图。
     * 如果a和b都不是系统最小，直接采用上面写好的div
     *
     * 系统最小 ÷ -1，按道理应该是系统最大值+1的，但是这个值没办法表示，越界了。
     * leetcode约定，这时返回最大值就行了。
     *
     * @param a
     * @param b
     * @return
     */
    public static int divide(int a, int b) {
        if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
            return 1;
        } else if (b == Integer.MIN_VALUE) {
            return 0;
        } else if (a == Integer.MIN_VALUE) {
            if (b == negNum(1)) {
                return Integer.MAX_VALUE;
            } else {
                int ans = div(add(a, 1), b);
                return add(ans, div(minus(a, multi(ans, b)), b));
            }
        } else {
            return div(a, b);
        }
    }

    public static void main(String[] args) {
        int a = 7;
        int b = -3;
        System.out.println(multi(a, b));
    }

}

 

 

 

 

 

 

 

 

 

 

 

 

 

 

--