Persistent Data Structures(可持久化的数据结构)
Persistent Data Structures
可持久化的数据结构
Contents
内容
- Introduction 介绍
- Persistent Singly Linked Lists 可持久化单向链表
- Persistent Binary Trees 可持久化二叉树
- Random Access Lists 随机存取列表
- ImmutableCollections 不可变类型集合类
- Stack 堆栈
- SortedList 有序列表
- ArrayList 动态数组
- Array 数组
- RandomAccessLists 随机存取列表
- Conclusion 结论
Introduction
介绍
When you hear the word persistence in programming, most often, you think of an application saving its data to some type of storage, such as a database, so that the data can be retrieved later when the application is run again. There is, however, another meaning for the word persistence when it is used to describe data structures, particularly those used in functional programming languages. In that context, a persistent data structure is a data structure capable of preserving the current version of itself when modified. In essence, a persistent data structure is immutable.
当你在编程过程中听到持久化这个单词的时候,大多数情况下,你会认为是应用程序将其数据为存储为某种类型的文件中,例如数据库,以便于以后当应用程序再次运行时能够从介质中重新获取数据。然而这里的持久化讲的是另外一个意思,用其来描述一种数据结构,通常会用在一些函数式的编程语言中。从这个意义上来讲,一个具有持久化能力的数据结构在其被修改后可以保存当前的状态,从本质上来说,这样的数据结构是不可改变类型(immutable)。
An example of a class that uses this type of persistence in the .NET Framework is the string class. Once a string object is created, it cannot be changed. Any operation that appears to change a string generates a new string instead. Thus, each version of a string object can be preserved. An advantage for a persistent class like the string class is that it basically gives you undo functionality built-in. As newer versions of a persistent object are created, older versions can be pushed onto a stack and popped off when you want to undo an operation. Another advantage is that because persistent data structures cannot change state, they are easier to reason about and are thread safe.
.NET Framework中的String类正好是使用了持久化能力的一个例子。一旦创建了一个String类型实例,它便不能被改变了,对于欲改变其值的任何操作都将被产生一个新的String对象,通过这样,每一个版本的String实例都将被驻留下来。这样的具有持久化特点的类型像String类型都内置了撤销(Undo)功能,当该对象的新一个版本产生的时候,旧版本将被压入栈中,如果需要执行撤销动作的时候,只需将旧版本从堆栈中取出。另外一个优点是由于可持久化数据类型不能更改其内部状态,很容易得知它是线程安全的。
There is an overhead that comes with persistent data structures, however. Each operation that changes a persistent data structure creates a new version of that data structure. This can involve a good deal of copying to create the new version. This cost can be mitigated to a large degree by reusing as much of the internal structure of the old version in creating a new one. I will explore this idea in making two common data structures persistent: the singly linked list and the binary tree, and describe a third data structure that combines the two. I will also describe several classes I have created that are persistent versions of some of the classes in the System.Collections namespace.
然而持久化的数据结构会带来一些开销,任何改变持久化数据结构的操作都将创建一个新的版本,这可能会涉及到大量的拷贝操作,通常我们可以通过重用旧版本对象的内部数据结构来创建一个新的对象,这种办法可以极大地降低拷贝操作所带来的消耗。我将会通过两个常用的数据结构来阐述这个思想:单向列表以及二叉树,然后通过这两个数据结构来组合第三个数据结构。同时我也会讲述System.Collection命名空间下面的那些持久化的类型。
Persistent Singly Linked Lists
持久化的单向链表
The singly linked list is one of the most widely used data structures in programming. It consists of a series of nodes linked together one right after the other. Each node has a reference to the node that comes after it, and the last node in the list terminates with a null reference. To traverse a singly linked list, you begin at the head of the list and move from one node to the next until you have reached the node you are looking for or have reached the last node:
单向链表是一个在编程中使用非常广泛的基础数据结构,它是由一系列相互链接的节点组成。每一个节点都拥有一个指向下一个节点的引用,链表中的最后一个节点将拥有一个空引用。如果你想遍历一个单向链表,可以从第一个节点开始,逐个向后移动,直到到达最后的节点。
如下图所示:
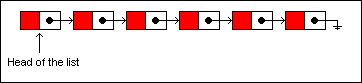
Let's insert a new item into the list. This list is not persistent, meaning that it can be changed in-place without generating a new version. After taking a look at the insertion operation on a non-persistent list, we'll look at the same operation on a persistent list.
让我们插入一个新的节点到这个链表中去,并且该链表是非持久化的,也就是说这个链表可以被改变而无需产生一个新的版本。在查看了非持久化链表的插入操作之后,我们将会查看同样的操作在持久化链表中。
Inserting a new item into a singly linked list involves creating a new node:
插入一个新的节点到单向列表中会涉及到创建一个新的节点:
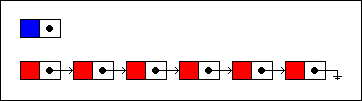
We will insert the new node at the fourth position in the list. First, we traverse the list until we've reached that position. Then the node that will precede the new node is unlinked from the next node...
我们将会在第四个位置插入新的节点,第一我们遍历链表到达指定位置,也就是插入节点前面的那个节点,将其与后面节点断开。
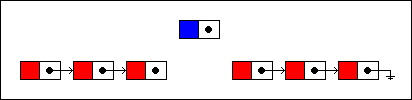
...and relinked to the new node. The new node is, in turn, linked to the remaining nodes in the list:
然后链接该节点与待插入节点,在下来,链接新的节点与上一步剩余的节点。

Inserting a new item into a persistent singly linked list will not alter the existing list but create a new version with the item inserted into it. Instead of copying the entire list and then inserting the item into the copy, a better strategy is to reuse as much of the old list as possible. Since the nodes themselves are persistent, we don't have to worry about aliasing problems.
如果插入一个新的节点到持久化的单向链表中,我们不应该改变当前链表的状态,而需要创建一个新的链表而后插入指定节点。相对于拷贝当前链表,而后插入指定节点,一个更好的策略是尽可能的重用旧的链表。因为节点本身是可持久化的,所以我们不必担心对象混淆的问题。
To insert a new node at the fourth position, we traverse the list as before only copying each node along the way. Each copied node is linked to the next copied node:
为了插入新节点到第四个位置,我们遍历链表到指定位置,拷贝每个遍历节点,同时指定拷贝的节点指向其下一个节点的拷贝。
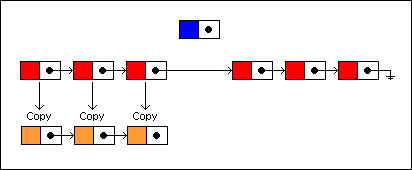
The last copied node is linked to the new node, and the new node is linked to the remaining nodes in the old list:
最后一个拷贝的节点指向新的插入节点,而后,新节点指向旧链表剩下的节点。
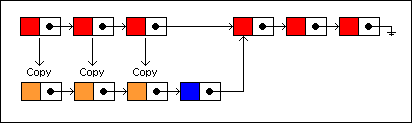
On an average, about N/2 nodes will be copied in the persistent version for insertions and deletions, where N equals the number of nodes in the list. This isn't terribly efficient but does give us some savings. One persistent data structure where this approach to singly linked list buys us a lot is the stack. Imagine the above data structure with insertions and deletions restricted to the head of the list. In this case, N nodes can be reused for pushing items onto a stack and N - 1 nodes can be reused for popping a stack.
平均来看,对于插入和删除操作,大约有N/2的节点将被拷贝,而N等于链表长度。这并不是特别的高效,仅仅只是节省了一些空间。与通过这样的方式来构建单向链表一样的一个数据结构是堆栈,我们可以想象一下在链表起始位置的插入以及删除操作,在这个场景中,对于堆栈来讲,压栈操作时全部节点都可以被重用,而出栈操作也有N-1个节点被重用。
Persistent Binary Trees
持久化二叉树
A binary tree is a collection of nodes in which each node contains two links, one to its left child and another to its right child. Each child is itself a node, and either or both of the child nodes can be null, meaning that a node may have zero to two children. In the binary search tree version, each node usually stores a key/value pair. The tree is searched and ordered according to its keys. The key stored at a node is always greater than the keys stored in its left descendents and always less than the keys stored in its right descendents. This makes searching for any particular key very fast.
一个二叉树是一系列节点的集合,每一个节点都包含有两个子节点,一个称之为左节点,而另一个称之为右节点。而子节点也是这样一个节点,也有一个左节点和一个右节点,当然也可以没有子节点,也就是说一个节点可能有零个或者两个子节点。在二叉查找树中,每一个节点通常包含了一个键值对,树结构将会依照节点的键来进行查找和组织。节点的键会永远大于其左节点的键,永远小于其右节点的键,这将使得对于特定键的查找非常迅速。
Here is an example of a binary search tree. The keys are listed as numbers; the values have been omitted but are assumed to exist. Notice how each key as you descend to the left is less than the key of its predecessor, and vice versa as you descend to the right:
下图是一个二叉查找树的例子,节点的键作为数字被列出,而节点的值则被忽略尽管是始终存在的。注意到每一个左边节点的键值一定会小于它的父节点即前驱节点,而每一个右边节点的键值一定大于其父节点键值。
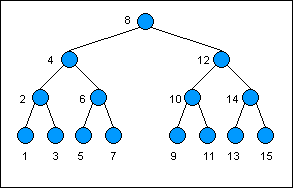
Changing the value of a particular node in a non-persistent tree involves starting at the root of the tree and searching for a particular key associated with that value, and then changing the value once the node has been found. Changing a persistent tree, on the other hand, generates a new version of the tree. We will use the same strategy in implementing a persistent binary tree as we did for the persistent singly linked list, which is to reuse as much of the data structure as possible when making a new version.
如果在一个非持久化的树中更改一个特定节点的值,我们会从根节点按照特定键值开始搜索,如果找到则直接更改该节点的值。但是如果是在一个持久化的树上的话,换句话说,我们需要创建一个新版本的树,同时还需要保持同实现一个持久化的二叉树或者单向链表一样的策略,即尽可能的重用当前的数据来创建一个新的版本。
Let's change the value stored in the node with the key 7. As the search for the key leads us down the tree, we copy each node along the way. If we descend to the left, we point the previously copied node's left child to the currently copied node. The previous node's right child continues to point to nodes in the older version. If we descend to the right, we do just the opposite.
下面让我们来尝试改变键为7的节点的值,按照自顶向下查找该节点的路径,我们需要拷贝该路径上的每一个节点。如果转向左边,需要将上一个拷贝的节点指向当前拷贝节点,而前一个节点的右侧节点则继续指向原来旧版本的节点。如果转向右边,则采用相反的做法。
This illustrates the "spine" of the search down the tree. The red nodes are the only nodes that need to be copied in making a new version of the tree:
下图列出了在树上自顶向下搜索特定节点的路径,在构建新版本的树的时候仅仅需要拷贝那些红色的节点。
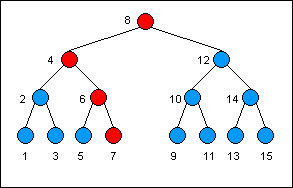
You can see that the majority of the nodes do not need to be copied. Assuming the binary tree is balanced, the number of nodes that need to be copied any time a write operation is performed is at most O(Log N), where Log is base 2. This is much more efficient than the persistent singly linked list.
你能够发现大多数节点是不要拷贝的,假定二叉树是平衡的,在每一次节点值的写操作中需要拷贝的节点数目大约是O(LogN),对数的底为2。显然比起持久化的单向链表效率很高。
Insertions and deletions work the same way, only steps should be taken to keep the tree in balance, such as using an AVL tree. If a binary tree becomes degenerate, we run into the same efficiency problems as we did with the singly linked list.
插入以及删除操作将按照同样的方式进行,但是一些额外的保持树平衡的操作还是必须的,例如使用AVL树作为底层数据结构的时候。如果二叉树变得很不平衡,我们将会碰到同样的效率问题如同在持久化单向链表是一样。
Random Access Lists
An interesting persistent data structure that combines the singly linked list with the binary tree is Chris Okasaki's random-access list. This data structure allows for random access of its items as well as adding and removing items from the beginning of the list. It is structured as a singly linked list of completely balanced binary trees. The advantage of this data structure is that it allows access, insertion, and removal of the head of the list in O(1) time as well as provides logarithmic performance in randomly accessing its items.
一个比较有意思的持久化数据结构是Chris Okasaki的随机存取列表,它结合了单向链表和二叉树的特点。这个数据结构除了允许用户随机操作其节点外,还支持在列表的起始位置添加和删除节点。它被组织成为一个使用二叉树来平衡的单向链表,其优点是当在其起始位置进行节点操作时,只需要O(1)的复杂度,而在随机操作节点的时候,也只有O(Log(N)).
Here is a random-access list with 13 items:
下面是一个具有13个子节点的随机存取列表:
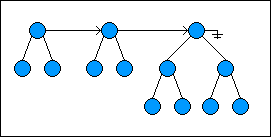
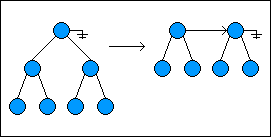
When a node is added to the list, the first two root nodes (if they exist) are checked to see if they both have the same height. If so, the new node is made the parent of the first two nodes; the current head of the list is made the left child of the new node, and the second root node is made the right child. If the first two root nodes do not have the same height, the new node is simply placed at the beginning of the list and linked to the next tree in the list.
当添加一个节点到列表中的时候,前两个根节点会被查看它们的高度是否相同,如果是的话,那新的节点将是这两个节点的父节点,第一个节点将会作为插入节点的左子节点,而第二个节点会作为右节点。而如果这两个节点高度不同,新的节将会直接被放在节点的起始位置,然后链接到剩余节点。
To remove the head of the list, the root node at the beginning of the list is removed, with its left child becoming the new head and its right child becoming the root of the second tree in the list. The new head of the list is right linked with the next root node in the list:
如果要删除链表的头节点,也就是要删除链表的起始根节点,然后将其左侧子节点作为新的头节点,而右侧子节点则作为链表中第个树的根节点。新的头节点会指向链表中向右的第二个根节点。
The algorithm for finding a node at a specific index is in two parts: in the first part, we find the tree in the list that contains the node we're looking for. In the second part, we descend into the tree to find the node itself. The following algorithm is used to find a node in the list at a specific index:
按照特定的索引查找节点的算法分为两个步骤,第一步我们找到在列表中包含制定节点的树,第二步自顶向下查找节点。下面的算法就是在列表中按照特定索引查找节点:
- Let I be the index of the node we're looking for. Set T to the head of the list where T will be our reference to the root node of the current tree in the list we're examining.
假定I是我们要查找的节点的索引,而T是列表的头节点,通过T我们就可以找到列表中当前树的根节点。
- If I is equal to 0, we've found the node we're looking for; terminate algorithm. Else if I is greater than or equal to the number of nodes in T, subtract the number of nodes in T from I and set T to the root of the next tree in the list and repeat step 2. Else if I is less than the number of nodes in T, go to step 3.
如果I等于0,则我们已经找到了要查找的节点。如果I大于等于节点T的子节点数目,从I中减去T的节点数目,然后将T作为下一个数的根节点,重复第二部。如果I小于T,跳转至第三步。
- Set S to the number of nodes in T divided by 2 (the fractional part of the division is ignored. For example, if the number of nodes in the current subtree is 3, S will be 1).
设定S为节点T子节点数目的一半,除法的小数部分将被忽略,如果节点数目为3,则S为1。
- If I is less than S, subtract 1 from I and set T to T's left child. Else subtract (S + 1) from I and set T to T's right child.
如果I小于S,I减一,然后设定T为T的左侧子节点;否则I减去(S+1),然后设定T为T的右侧子节点。
- If I is equal to 0, we've found the node we're looking for; terminate algorithm. Else go to step 3.
如果I等于0,则我们已经找到了要查找的节点,否则跳转至第三步。
This illustrates using the algorithm to find the 10th item in the list:
下图描述了使用上面的算法来找到列表中第十个节点。
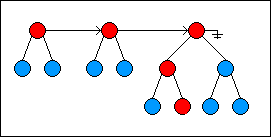
Keep in mind that all operations that change a random-access list do not change the existing list but rather generate a new version representing the change. As much of the old list is reused in creating a new version.
记住所有改变随机存取列表的操作都不会改变现有列表,而是创建一个新的版本,并且在创建新版本的时候要尽可能充用现有列表。
Immutable Collections
不可改变集合类型
Included with this article are a number of persistent collection classes I have created. These classes are in a namespace called ImmutableCollections. I have created persistent versions of some of the collection classes in the System.Collections namespace. I will describe each one and some of the challenges in making them persistent. There are several collection classes that are currently missing; I need to add a queue, for example. Hopefully, I will get to those in time. Also, even though I've taken steps to make these classes efficient, they cannot compete with the System.Collections classes in terms of speed, but they really aren't meant to. They are meant to provide the advantages of immutability while providing reasonable performance.
在本文中我创建了许多持久化的集合类型,放在命名空间ImmutableCollections下。对于System.Collection命名空间下的一些集合类,我也创建了一个持久化的版本。我将会逐个讲述这些类型,阐述在持久化这些类时所遇到的问题及挑战。当然有一些遗漏的,例如Queue。希望有时间我能够将它们补上。尽管我已经采取了一些措施来提高性能,在存取速度上这些类还是不能与System.Collection命名空间的类相比较,但是这些类具有不可变类型的优点,而且具有合理的可以接收的性能。
Stack
堆栈
This one was easy. Simply create a persistent singly linked list and limit insertions and deletions to the head of the list. Since this class is persistent, popping a stack returns a new version of the stack with the next item in the old stack as the new top. In the System.Collections.Stack version, popping the stack returns the top of the stack. The question for the persistent version was how to make the top of the stack available since it cannot be returned when the stack is popped. I chose to create a Top property that represents the top of the stack.
这个类是比较容易的,可以创建一个持久化的单向链表,然后限定只能在起始位置进行插入和删除操作。因为这个类是持久化的,出栈操作将会返回一个新版本的堆栈,这个堆栈以旧堆栈的第二个节点为头节点。在System.Collection命名空间下,出栈操作仅仅只是删除栈顶元素并返回。
SortedList
有序列表
The SortedList uses AVL tree algorithms to keep the tree in balance. I found it useful to create an IAvlNode interface. Two classes implement this interface, the AvlNode class and the NullAvlNode class. The NullAvlNode class implements the null object design pattern. This simplified many of the algorithms.
有序列表使用了AVL树的算法来保持树节点的平衡,我创建了一个叫IAvlNode的接口,有两个类实现了这个接口,它们分别是AvlNode以及NullAvlNode类。NullAvlNode类利用了Null对象的设计模式,这将会简化一些算法。
ArrayList
动态数组
This is the class that proved most challenging. Like the SortedList, it uses a persistent AVL tree as its data structure. However, unlike the SortedList, items are accessed by index (or by position) rather than by key. I have to admit that the algorithms for accessing and inserting items in a binary tree by index weren't intuitive to me, so I turned to Knuth. Specifically, I used Algorithms B and C in section 6.2.3 in volume 3 of The Art of Computer Programming.
这个类的实现会遇到更多的挑战。与有序列表相同的是它也使用了持久化的AVL树来作为其底层的数据结构,不同的地方是是用户只能通过顺序索引来操作列表元素而不是字符串索引。不得不说的是我的本意并不是在一个二叉树上按照顺序索引来操纵和插入列表元素,所以我查看了Knuth的书籍,准确地来讲是使用了计算机编程的艺术第三卷6.2.3中的算法B和C。
I made an assumption about the ArrayList in order to improve performance. I assumed that the Add method is by far the most used method. However, adding items to the ArrayList one right after the other causes a lot of tree rotations to keep the tree in balance. To solve this, I created a template tree that is already completely balanced. Since this template tree is immutable, it can exist at the class level and be shared amongst all of the instances of the class.
为了提高动态数组的性能,我做了一个假设。假定Add方法是动态数组使用最多的方法,然而为了保持树的平衡,添加对象操作会引起多次的树旋转。为了解决这个问题,我创建了一个完全平衡的模板树,因为这个树是不可更改的,它可以在类的级别上存在,且能够被所有类的实例所共享。
When an instance of the ArrayList class is created, it takes a small subtree of the template tree. As items are added, the nodes in the template tree are replaced with new nodes. Since the tree is completely balanced, no rebalancing is necessary. If the subtree gets filled up, another subtree of equal height is taken from the template tree and joined to the existing tree. Insertions and deletions are handled normally with rebalancing performed if necessary. Again, the assumption is that adding items to the ArrayList occurs much more frequently than inserting or deleting items.
当一个动态数组的实例被创建的时候,它会抓住模板树的一个子树。当添加子节点的时候,模板树上的节点将会被新添的节点所替换,因为模板树本身就是平衡的,所以无需平衡树的操作。如果这个子树已经被填满,则会在模板树上抓取高度相同的另外一个子树,然后加入当前存在的树。当然插入和删除操作就需要进行平衡操作了。再一次强调的是我们的假设是添加节点的操作会远多于插入以及删除操作,才可以这样做。
Array
数组
The Array class uses the random access list structure to provide a persistent array with logarithmic performance. Unlike a random access list, it has a fixed size.
数组类使用随机存取列表作为基础的数据结构,而随机存取列表在进行查找的时候只有Log(N)的复杂度,与随机存取列表不同的是,数据具有固定的长度。
RandomAccessList
随机存取列表
This class does not have a parallel in the System.Collections namespace, but it was one of the first persistent classes I wrote, and I decided to include it here. It's a straightforward implementation of Chris Okasaki's random-access list described above. This data structure was designed to be used in functional languages where lists have three basic operations: Cons, Head, and Tail. Cons adds an item to the head of the list, Head is the first item in the list, and Tail represents all of the items in the list except for the Head.
这个类型在.NET类库的System.Collection命名空间下没有对应的实现类,但是它是我写的第一个持久化类,所以我决定在这里也介绍一下。在Chris Okasaki的文章中有一个简单易懂的实现,在一些函数式语言中会经常用到这个数据结构,通常它有三个基本操作:Cons,Head和Tail,Cons会添加一个新的对象到这个列表对象的开头,而Head将会返回列表的第一个对象,通过Tail会得到列表中除了第一个对象外的所有对象。
Conclusion
结论
Persistent data structures help simplify programming by eliminating a whole class of bugs associated with side-effects and synchronization issues. They are not a cure-all but are a useful tool for helping a programmer deal with complexity. I have explored ways of making data structures persistent and have provided a small .NET library of persistent data structures. I hope you have enjoyed the article, and as always, I welcome feedback.
持久化数据结构会有助于简化编程,将一些线程同步的问题消除掉。它并不是解救一切的灵丹妙药,而是帮助程序员减低程序复杂度的一个工具。我已经阐述了如何构建持久化数据的多种方法,并且打包成一个小的.NET类库。我希望你能够从本文中受益,并且永远欢迎您的反馈信息。
2008.11.13 更新:
原帖地址 :http://www.codeproject.com/KB/recipes/persistentdatastructures.aspx
大家可以从原帖中下载相关代码。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号