R语言近似贝叶斯计算MCMC（ABC-MCMC）轨迹图和边缘图可视化

原文链接：http://tecdat.cn/?p=26336 

原文出处：拓端数据部落公众号

近似贝叶斯计算和近似技术基于随机模拟模型中的样本计算近似似然值，在过​​去几年中引起了很多关注，因为它们有望为任何随机过程提供通用统计技术。

一位同事向我询问我们在我们的文章中讨论过的近似贝叶斯计算 MCMC (ABC-MCMC) 算法的简单示例。下面，我提供了一个最小的示例，类似于Metropolis-Hastings 。

1.  
   library(coda)
2.  
    
3.  
    
4.  
    
5.  
    
6.  
    
7.  
   # 假设数据是正态分布的10个样本
8.  
    
9.  
   # 平均值为5.3，SD为2.7
10.  
     
11.  
    data =  rnorm
12.  
     
13.  
     
14.  
     
15.  
     
16.  
     
17.  
    # 我们想用ABC来推断出所使用的参数。
18.  
     
19.  
    # 我们从同一个模型中取样，用平均值和方差作为汇总统计。当我们接受ABC时，我们返回真，因为与数据的差异小于某个阈值
20.  
     
21.  
     
22.  
     
23.  
     
24.  
     
25.  
     
26.  
     
27.  
    ABC <- function(pr){
28.  
     
29.  
     
30.  
     
31.  
      # 先验避免负的标准偏差
32.  
     
33.  
      if (par <= 0) return(F)
34.  
     
35.  
     
36.  
     
37.  
      # 随机模型为给定的参数生成一个样本。
38.  
     
39.  
     
40.  
      samples <- rnorm
41.  
     
42.  
     
43.  
     
44.  
      # 与观察到的汇总统计数字的比较
45.  
     
46.  
     
47.  
      if((difmean < 0.1) & (difsd < 0.2)) return(T) else return(F)
48.  
     
49.  
    }
50.  
     
51.  
     
52.  
     
53.  
     
54.  
     
55.  
    # 我们将其插入一个标准的metropolis Hastings MCMC中。
56.  
     
57.  
    #用metropolis 的接受度来交换ABC的接受度
58.  
     
59.  
     
60.  
     
61.  
    MCMCABC <- function(saue, itns){
62.  
     
63.  
     
64.  
     
65.  
     
66.  
        for (i in 1:ieraos){
67.  
     
68.  
     
69.  
     
70.  
            # 提议函数
71.  
     
72.  
            prp = rnorm(2,mean = chain[i,], sd= c(0.7,0.7))
73.  
     
74.  
     
75.  
     
76.  
            if(A_ance(prl)){
77.  
     
78.  
                chn[i+1,] = prl
79.  
     
80.  
            }else{
81.  
     
82.  
                chn[i+1,] = cain[i,]
83.  
     
84.  
            }
85.  
     
86.  
        }
87.  
     
88.  
        return(mcmc(cin))
89.  
     
90.  
    }
91.  
     
92.  
     
93.  
     
94.  
    plot(psor)

结果应该是这样的：

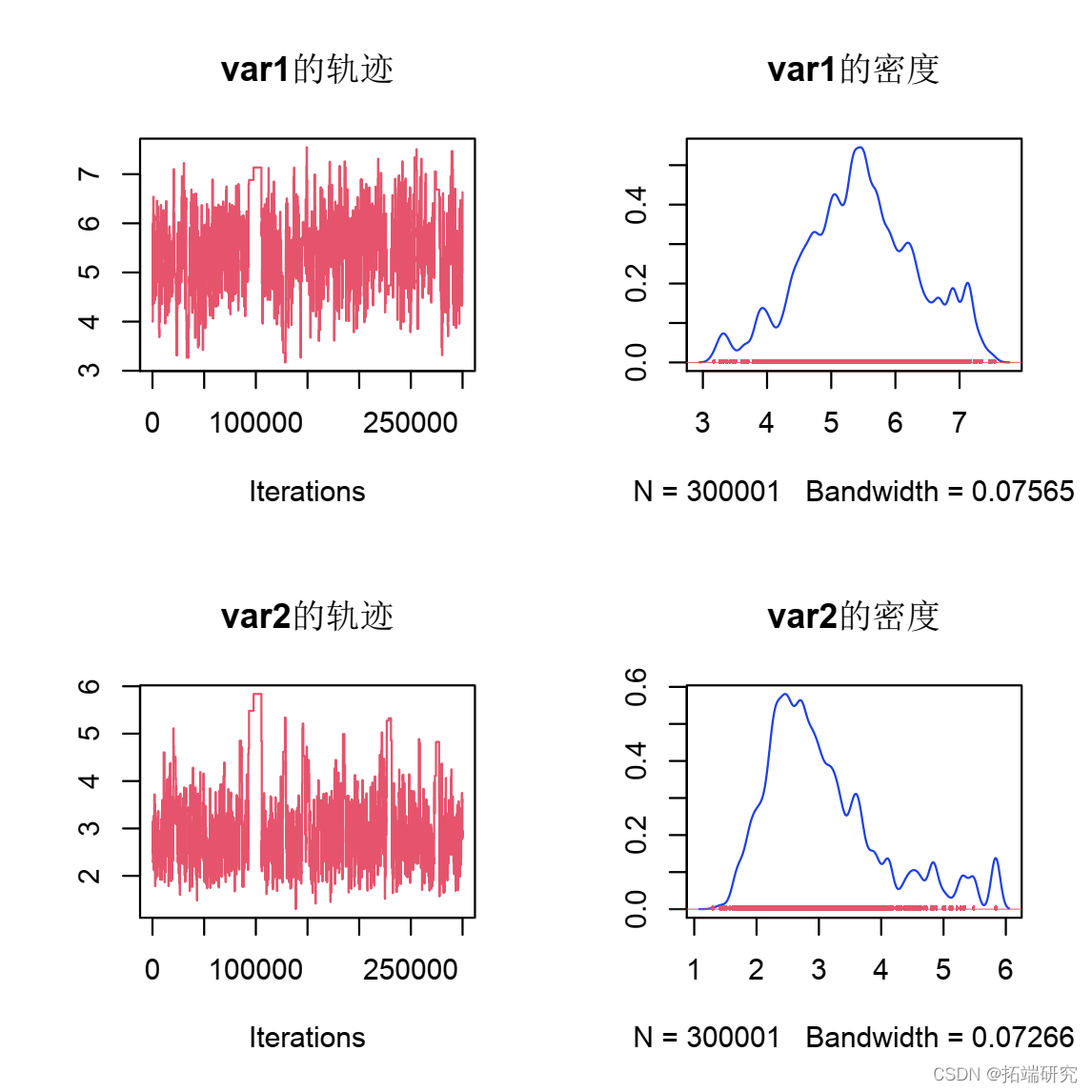
图：后验样本的轨迹图和边缘图。从右边的边缘图中，您可以看到我们正在近似检索原始参数值，即 5.3 和 2.7。

---

最受欢迎的见解

1.matlab使用贝叶斯优化的深度学习

2.matlab贝叶斯隐马尔可夫hmm模型实现

3.R语言Gibbs抽样的贝叶斯简单线性回归仿真

4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

5.R语言中的Stan概率编程MCMC采样的贝叶斯模型

6.Python用PyMC3实现贝叶斯线性回归模型

7.R语言使用贝叶斯 层次模型进行空间数据分析

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.matlab贝叶斯隐马尔可夫hmm模型实现