拓端tecdat|Matlab用BUGS马尔可夫区制转换Markov switching随机波动率SV模型、序列蒙特卡罗SMC、Metropolis Hastings采样分析时间序列数据

原文链接：http://tecdat.cn/?p=24498

原文出处：拓端数据部落公众号

在这个例子中，我们考虑马尔可夫转换随机波动率模型。

统计模型

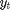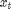让  是因变量和  未观察到的对数波动率 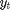. 随机波动率模型定义如下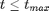 

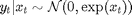
区制变量  遵循具有转移概率的二态马尔可夫过程

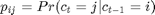
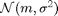 表示均值的正态分布  和方差 .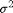

BUGS语言统计模型

文件“ssv.bug”的内容：

1.  
   file = 'ssv.bug'; % BUGS模型文件名
2.  
    
3.  
   model
4.  
   {
5.  
   x[1] ~ dnorm(mm[1], 1/sig^2)
6.  
   y[1] ~ dnorm(0, exp(-x[1]))
7.  
    
8.  
   for (t in 2:tmax)
9.  
   {
10.  
    c[t] ~ dcat(ifelse(c[t-1]==1, pi[1,], pi[2,]))
11.  
    mm[t] <- alp[1] * (c[t]==1) + alp[2]*(c[t]==2) + ph*x[t-1]

安装

1. 下载Matlab最新版本
2. 将存档解压缩到某个文件夹中
3. 将程序文件夹添加到 Matlab 搜索路径

addpath(path)

通用设置

1.  
    
2.  
   lightblue
3.  
   lightred
4.  
    
5.  
   % 设置随机数生成器的种子以实现可重复性
6.  
   if eLan 'matlab', '7.2')
7.  
   rnd('state', 0)
8.  
   else
9.  
   rng('default')
10.  
    end

加载模型和数据

模型参数

1.  
   tmax = 100;
2.  
   sig = .4;

解析编译BUGS模型，以及样本数据

1.  
   model(file, data, 'sample', true);
2.  
   data = model;

绘制数据

1.  
   figure('nae', 'Lrtrs')
2.  
   plot(1:tmax, dt.y)

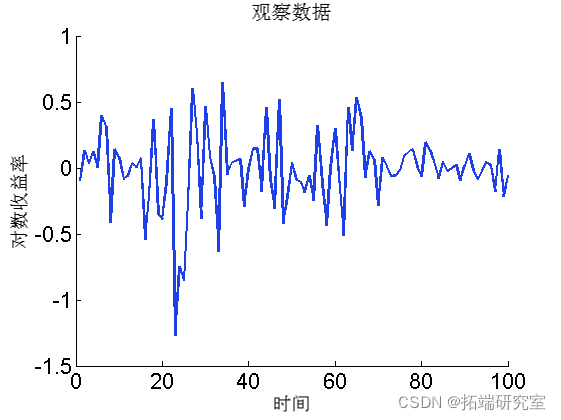
Biips 序列蒙特卡罗SMC

运行SMC

1.  
   n_part = 5000; % 粒子数
2.  
   {'x'}; % 要监控的变量
3.  
   smc = samples（npart）；

算法的诊断。

diag   (smc);

 

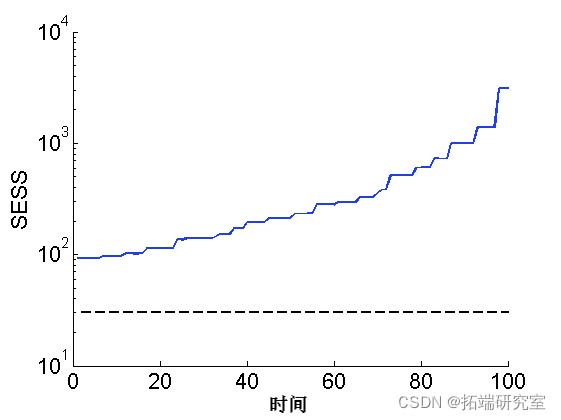
绘图平滑 ESS

1.  
    
2.  
   sem(ess)
3.  
    
4.  
   plot(1:tmax, 30*(tmax,1), '--k')
5.  
    

绘制加权粒子

1.  
    
2.  
   for ttt=1:tttmax
3.  
   va = unique(outtt.x.s.vaues(ttt,:));
4.  
    
5.  
   wegh = arrayfun(@(x) sum(outtt.x.s.weittt(ttt, outtt.x.s.vaues(ttt,:) == x)), va);
6.  
    
7.  
   scatttttter(ttt*ones(size(va)), va, min(50, .5*n_parttt*wegh), 'r',...
8.  
   'markerf', 'r')
9.  
   end

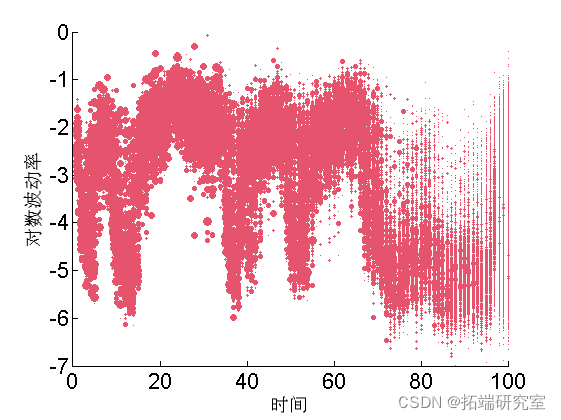
汇总统计

summary(out, 'pro', [.025, .975]);

绘图滤波估计

1.  
   mean = susmc.x.f.mean;
2.  
   xfqu = susmc.x.f.quant;
3.  
   h = fill([1:tmax, tmax:-1:1], [xfqu{1}; flipud(xfqu{2})], 0);
4.  
    
5.  
   plot(1:tmax, mean,)
6.  
   plot(1:tmax, data.x_true)

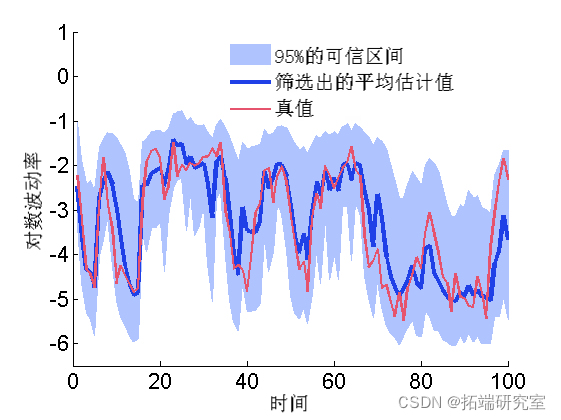
绘图平滑估计

1.  
    
2.  
   mean = smcx.s.mean;
3.  
   quant = smcx.s.quant;
4.  
    
5.  
   plot(1:t_max, mean, 3)
6.  
   plot(1:t_max, data.x_true, 'g')

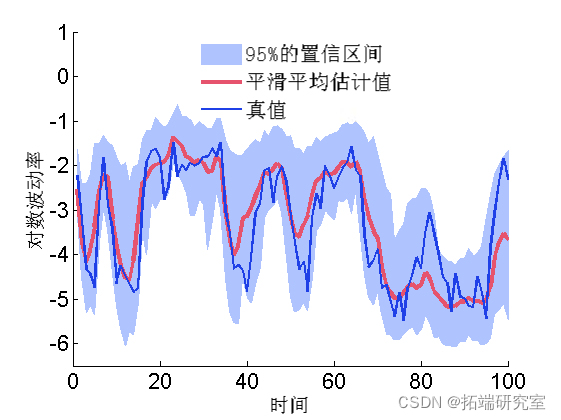
边际滤波和平滑密度

1.  
   kde = density(out);
2.  
   for k=1:numel(time)
3.  
   tk = time(k);
4.  
   plot(kde.x.f(tk).x, kde.x.f(tk).f);
5.  
   hold on
6.  
   plot(kde.x.s(tk).x, kde.x.s(tk).f, 'r');
7.  
   plot(data.xtrue(tk));
8.  
   box off
9.  
   end

Biips 粒子独立 Metropolis-Hastings

PIMH 参数

1.  
    
2.  
   thi= 1;
3.  
   nprt = 50;

运行 PIMH

1.  
   init(moel, vaibls);
2.  
   upda(obj, urn, npat); % 预烧迭代
3.  
   sample(obj,...
4.  
   nier, npat, 'thin', thn);

一些汇总统计

summary(out, 'prs');

后均值和分位数

1.  
   mean = sumx.man;
2.  
   quant = su.x.qunt;
3.  
    
4.  
   hold on
5.  
   plot(1:tax, man, 'r', 'liith', 3)
6.  
   plot(1:tax, xrue, 'g')

MCMC 样本的踪迹

1.  
    
2.  
   for k=1:nmel(timndx)
3.  
   tk = tieinx(k);
4.  
   sublt(2, 2, k)
5.  
   plot(outm.x(tk, :), 'liedh', 1)
6.  
   hold on
7.  
   plot(0, d_retk), '*g');
8.  
   box off
9.  
   end

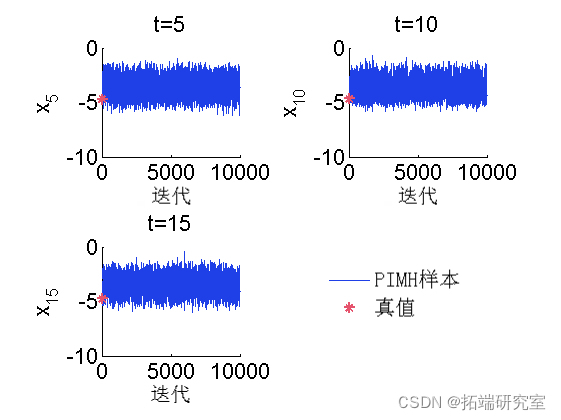
后验直方图

1.  
   for k=1:numel(tim_ix)
2.  
   tk = tim_ix(k);
3.  
   subplot(2, 2, k)
4.  
   hist(o_hx(tk, :), 20);
5.  
   h = fidobj(gca, 'ype, 'ptc'); hold on
6.  
   plot(daau(k), 0, '*g');
7.  
    
8.  
   box off
9.  
   end

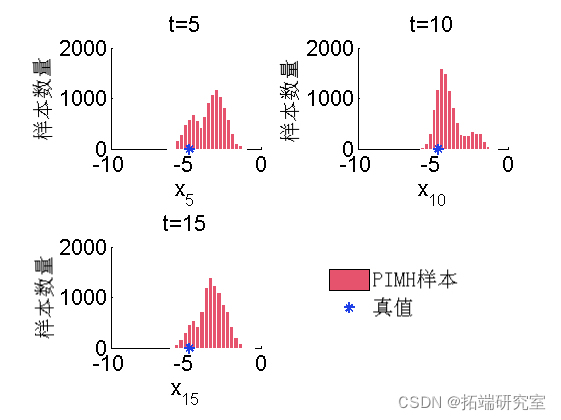
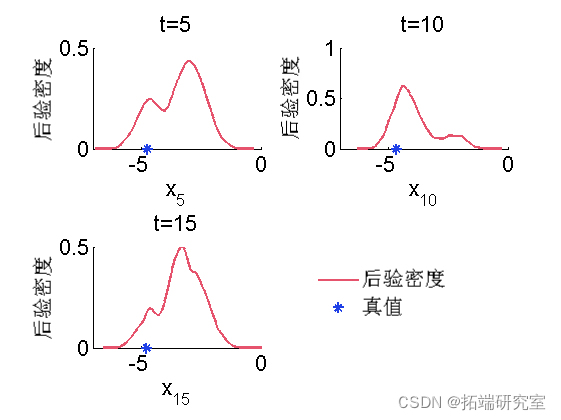
后验的核密度估计

1.  
   pmh = desity(otmh);
2.  
   for k=1:numel(tenx)
3.  
   tk = tim_ix(k);
4.  
   subplot(2, 2, k)
5.  
   plot(x(t).x, dpi.x(tk).f, 'r');
6.  
   hold on
7.  
   plot(xtrue(tk), 0, '*g');
8.  
   box off
9.  
   end

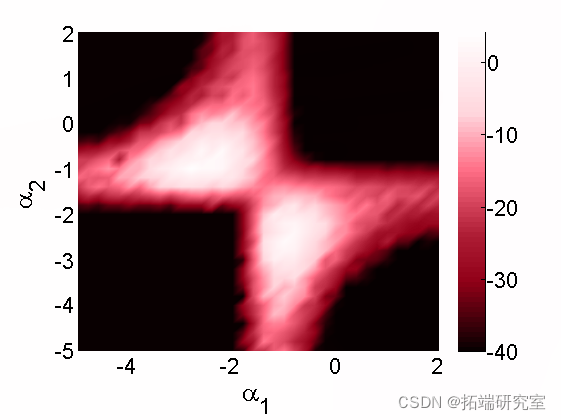
Biips 敏感性分析

我们想研究对参数值的敏感性 

算法参数

1.  
   n= 50; % 粒子数
2.  
   para = {'alpha}; % 我们要研究灵敏度的参数
3.  
   % 两个分量的值网格
4.  
   pvs = {A(:, B(:';

使用 SMC 运行灵敏度分析

smcs(modl, par, parvlu, npt);

绘制对数边际似然和惩罚对数边际似然率

1.  
   surf(A, B, reshape(ouma_i, sizeA)
2.  
   box off

---

最受欢迎的见解

1.用R语言模拟混合制排队随机服务排队系统

2.R语言中使用排队论预测等待时间

3.R语言中实现马尔可夫链蒙特卡罗MCMC模型

4.R语言中的马尔科夫机制转换(Markov regime switching)模型

5.matlab贝叶斯隐马尔可夫hmm模型

6.用R语言模拟混合制排队随机服务排队系统

7.Python基于粒子群优化的投资组合优化

8.R语言马尔可夫转换模型研究交通伤亡人数事故预测

9.用机器学习识别不断变化的股市状况——隐马尔可夫模型的应用