拓端tecdat|R语言辅导广义线性模型(GLMs)算法和零膨胀模型分析

原文链接：http://tecdat.cn/?p=14887 

广义线性模型（GLM） 是通过连接函数,把自变量线性组合和因变量的概率分布连起来,该概率分布可以是高斯分布、二项分布、多项式分布、泊松分布、伽马分布、指数分布。连接函数有：

• 平方根连接（用于泊松模型）

考虑一些均值μ和方差σ2的随机变量Y。利用泰勒展开式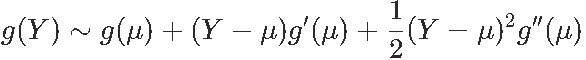

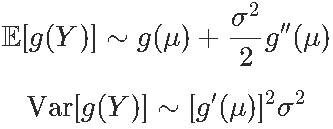
假使，考虑平方根变换g（y）= \ sqrt {y} g（y）= y，则第二个等式变为

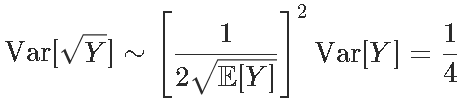
因此，通过平方根变换，我们具有方差稳定性，可以将其解释为一定的同调性。

• 伯努利模型的对数函数

假设变量是泊松变量，

先前的模型看起来像是伯努利回归分析，其中H作为链接函数，\ mathbb {P}

因此，现在假设代替观察N，我们观察到Y = 1（N> 0）。在那种情况下，运行带有对数链接函数的伯努利回归，首先与对原始数据运行泊松回归，然后在我们的二进制变量零和非零上使用。让我们先生成一些模拟数据，比较从标准逻辑回归得到的eλx和px

1.  
    
2.  
   regPois = glm(Y~.,data=base,family=poisson(link="log"))
3.  
   regBinom = glm((Y==0)~.,data=base,family=binomial(link="probit"))

 

 

 

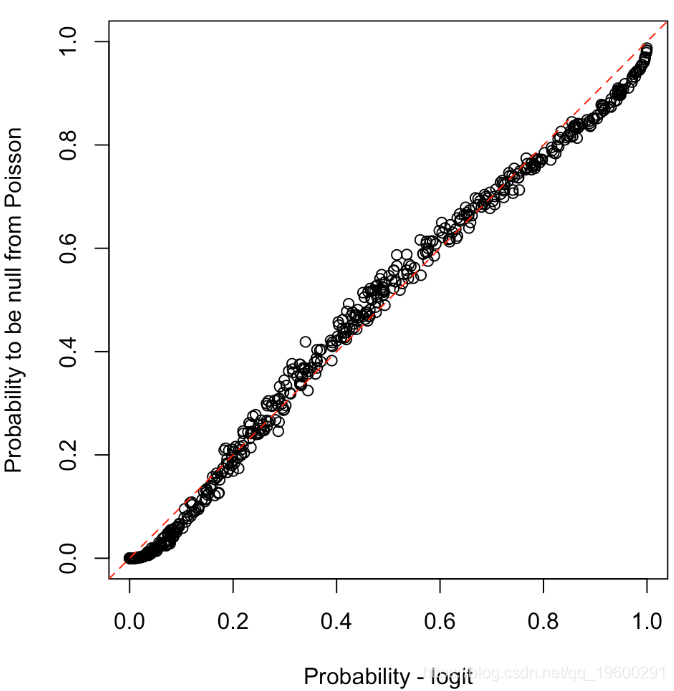
如果px \是从Bernoulli回归中获得的，并且具有连接功能，该怎么办？

1.  
    
2.  
   plot(prob,1-exp(-lambda),xlim=0:1,ylim=0:1)
3.  
   abline(a=0,b=1,lty=2,col="red")

 

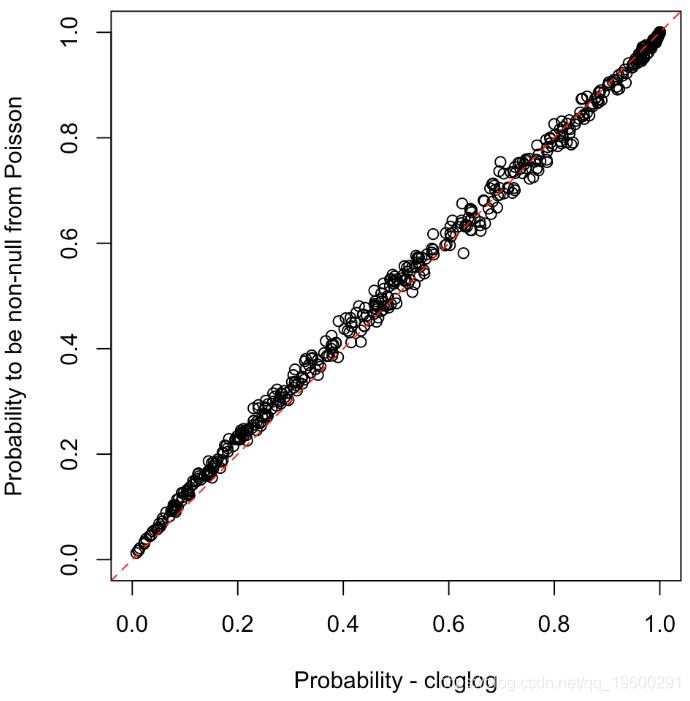
拟合很好，现在，如果我们对婚姻出轨数据集，由雷·费尔，在1978年出版的  期刊政治经济学  （含563个观察，九个变量）进行建模：

1.  
    
2.  
   prob = predict(regBinom, type="response")
3.  
   plot(prob,exp(-lambda),xlim=0:1,ylim=0:1)
4.  
   abline(a=0,b=1,lty=2,col="red")

 

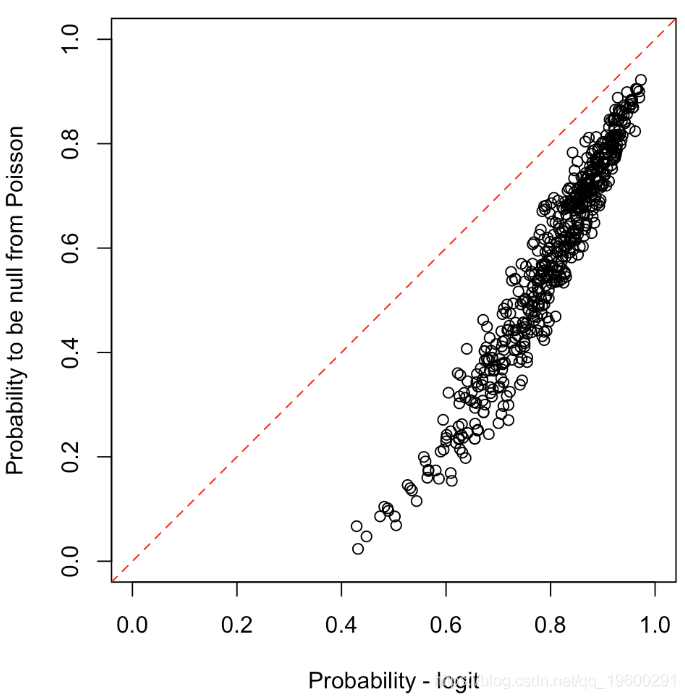
在这种情况下，这两种模型结果是非常不同的。第二个模型也是

1.  
    
2.  
   plot(prob,1-exp(-lambda),xlim=0:1,ylim=0:1)
3.  
   abline(a=0,b=1,lty=2,col="red")

 

 

 

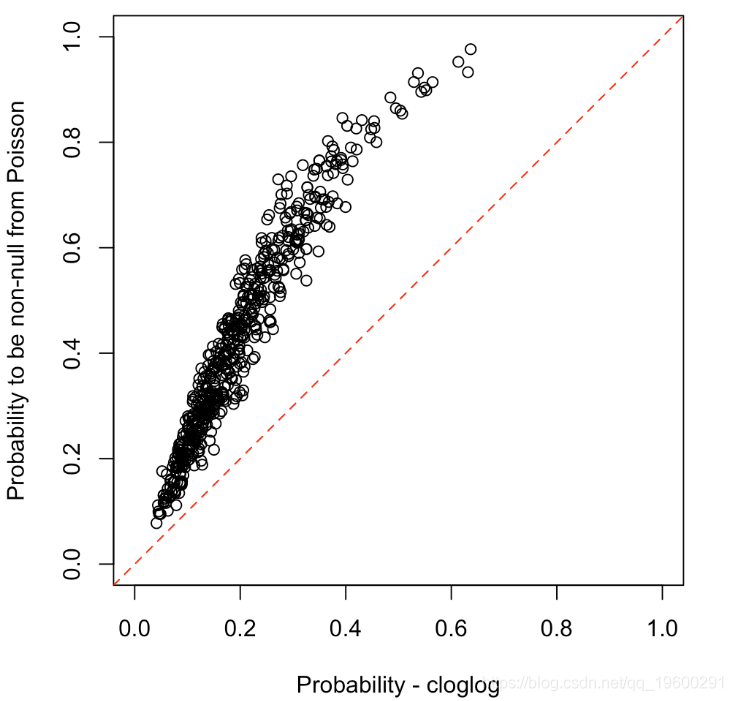
我们如何解释呢？是因为泊松模型不好吗？我们在这里运行零膨胀模型进行比较，

1.  
    
2.  
   summary(regZIP)
3.  
    
4.  
   Count model coefficients (poisson with log link):
5.  
   Estimate Std. Error z value Pr(>|z|)
6.  
   (Intercept) -0.002274 0.048413 -0.047 0.963
7.  
   X1 1.019814 0.026186 38.945 <2e-16 ***
8.  
   X2 1.004814 0.024172 41.570 <2e-16 ***
9.  
   Zero-inflation model coefficients (binomial with logit link):
10.  
    Estimate Std. Error z value Pr(>|z|)
11.  
    (Intercept) -4.90190 2.07846 -2.358 0.0184 *
12.  
    X1 -2.00227 0.86897 -2.304 0.0212 *
13.  
    X2 -0.01545 0.96121 -0.016 0.9872
14.  
    ---
15.  
    Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

由于零的膨胀，我们在这里拒绝了泊松分布的假设，可以使用对数连接来检查泊松分布是否是一个好的模型。