AT3527 [ARC082D] Sandglass

LUOGU AT3527 [ARC082D] Sandglass:
$$C^沙_漏$$

Problem:

有一个沙漏由两个上下相通玻璃球 $A$ 和 $B$ 构成，这两个玻璃球都含有一
定量的沙子，我们暂且假定 $AB$ 中位于上方的玻璃球的为 $U$，下方的玻璃
球为 $L$，则除非 $U$ 中没有沙子，否则每秒钟都会有$1$克沙子从 $U$ 掉入 $L$。

在第 $0$ 个时刻，$A$ 中有 $a$ 克沙子，$B$ 中有 $X−a$ 克沙子(总共有 $X$ 克沙子)，且 $U$ 为 $A$，$L$ 为 $B$ (即 $A$ 上 $B$ 下)。

在 $r_1,r_2,...,r_k$ 这些时刻，我们将倒转整个沙漏，使得原来的 $U$ 变成 $L$，原来的 $L$ 变成 $U$。对于翻转操作，$t$时刻是指从第 $0$ 个时刻起经过 $t$ 秒后的时刻，我们可以将翻转沙漏的操作看做瞬间完成的。

现在有 $Q$ 次询问，每一次询问会给定一对非负整数 $(t_i,a_i)$，求$a=a_i$，第 $t_i$ 时刻，A 中所含沙子的克数。

首先翻转一次可以看成是沙子从 $A$ 中的沙子数由增加变为减少或者由减少变为增加。

由于沙子总数 $X$ 不变, 所以我们可以通过 $A$ 中的沙子数反映 $B$ 中的沙子数。

设 $f_{s t}(t)$ 表示初始时 $A$ 中沙子数为 $s t$, 时间为 $t$ 秒时 $A$ 中剩余的沙子数。

那么我们把时间 $t$ 当为 $x$ 轴, $A$ 中的沙子数当作 $y$ 轴, 将初始时 $A$ 中沙子数为 $0 \sim X$ 的折线图像画出 来: $\quad$ (即 $f_{0 \sim X}$ 的图像)

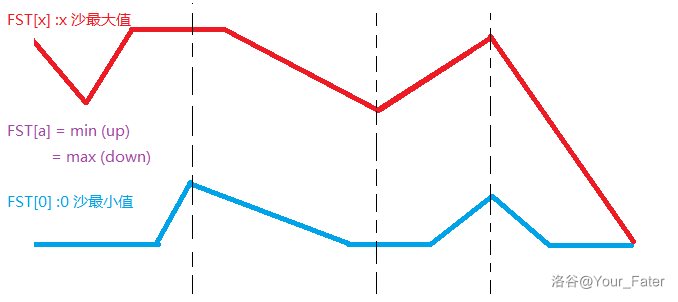
如图, 红线为初始时 $A$ 中沙子数为 $X$ 时的折线图像 $\left(f_{X}\right)$, 蓝线为初始时 $A$ 中沙子数为 $0$ 时的折线图 像
$\left(f_{0}\right)$ 。

发现不论初始时 $A$ 中有多少沙子, 对于任意时刻 $t$, 都有 $f_{0}(t) \leq f_{1}(t) \leq \cdots \leq f_{X}(t)_{。}$

那么对于询问 $\left(t_{i}, a_{i}\right)$, 有了 $f_{a_{i}}\left(t_{i}\right)$ 的上下界 $\left[f_{0}(t), f_{X}(t)\right]$, 就很好做了。

又发现如果折线 $f_{a_{i}}$ 在某一时刻触碰到了

$f_{0}\left(\right.$ 或者 $f_{X}$ ), 那么在这个时刻以后,

$f_{a_{i}}$ 的折线就和 $f_{0}$ ( $f_{X}$ ) 重合了。

所以当 $t \leq t_{i}$ 时，要么折线 $f_{a_{i}}$ 在 $t \leq t_{i}$ 的时候触碰到了 $f_{0}\left(f_{X}\right)$,

此时 $f_{a_{i}}\left(t_{i}\right)$ 就等于 $f_{0}\left(t_{i}\right)$

$\left.f_{X}\left(t_{i}\right)\right)$
要么折线 $f_{a_{i}}$ 在 $t \leq t_{i}$ 的时候没有 $f_{0}$ 或 $f_{X}$, 那这种情况怎么计算呢?

发现若 $f_{a_{i}}$ 触碰了 $f_{0}$ 或 $f_{X}$ 了 $f_{0}$, 触碰到 $f_{X}$ 是同理的 $)$,

肯定是在 $y=0$ 或 $y=X$ 的 时候碰到的, 因为只有当 $f_{0}$ 横着走， $f_{a_{i}}$ 斜着走的时候他们才会相遇, 且只有当 $f_{0}=0$ 或 $f_{0}=X$ 的 时候 $f_{0}$ 才会横若走。

所以当 $t \leq t_{i}$ 时，若 $f_{a_{i}}$ 没有 $f_{0}$ 或 $f_{X}$, 那么折线 $f_{a_{i}}$ 就肯定没有触碰过 $y=0$ 或 $y=X$, 也 就是说, 不存在任意一个时刻 $t\left(t \leq t_{i}\right)$, 使得沙漏 $A$ 或 $B$ 中没有沙子。

统计一下 sum， 然后加上 $a_{i}$ 就好了 (详见代码) 。

那么现在问题来了: 如何判断 $f_{a_{i}}$ 是否触碰 $f_{0}$ 或 $f_{X}$ ?

甚实很简单，我们先设此时 $f_{0}$ 答案为 down

$=f_{0}\left(t_{i}\right), f_{X}$ 答案为 $u$

$p=f_{X}\left(t_{i}\right)$, 那么此时答案的上下 界为 $[$ down,$u p]$ 。假设 $f_{a_{i}}$ 没有触碰过 $f_{0}$ 或 $f_{X}$ 时用 $s u m$ 算出来的答案 $t m p_{\circ}$

然后如果 $t m p>u p$, 答案就是 $u p ;$ 如果 $t m p<d o w n$, 答案就是 down $;$ 否则答案就是 $t m p_{\circ}$

因为如果你用 $s u m$ 算出来的折线某一时刻超过了 $y=0$ 或 $y=X$ ，那么它永远不可能回到区间 $[$ down,$u p]$, 除非此时 down $=u p_{\circ}$

那么我们只用维护 3 个值，就可以维护所有值的范围了: $f_{0}, f_{X}$, $sum$.

由于给出的 $r_{i}$ 和 $t_{i}$ 是递增的，所以可以在 $O(n+m)$ 的时间内维护。

上才艺:

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x;
	scanf("%d",&x);
	return x;
}
int main() {
	int x=read(),n=read(),a[100000+5];
	for(int i=1; i<=n; i++) a[i]=read();
	int m=read();
	int up=x/*最高点只能为x*/,down=0/*最低点为0*/,sum=0,tmp=0,tag/*靠经down或者up*/=-1;
	while(m--) {
		int t=read(),RES=read();
		while(tmp<n&&a[tmp+1]<=t) {
			down=min(x,max(0,down+tag*(a[tmp+1]-a[tmp])));
			up=min(x,max(0,up+tag*(a[tmp+1]-a[tmp])));
			sum=sum+tag*(a[tmp+1]-a[tmp]);
			tag=-tag,tmp++;
		}
		int down1=min(x,max(0,down+tag*(t-a[tmp])));
		int up1=min(x,max(0,up+tag*(t-a[tmp])));
		int sum1=sum+tag*(t-a[tmp]);
		printf("%d\n",min(up1,max(down1,sum1+RES)));
	}
	return 0;
}

咕咕，下班