(26/60)组合总和、组合总和Ⅱ、分割回文串

组合总和

leetcode：39. 组合总和

回溯法

思路

在组合的基础上，只不过同一个数字可以重复选取，递归时传入i即可（组合是传入i+1）。

复杂度分析

时间复杂度：

• 在最坏情况下，回溯算法会遍历所有可能的组合，因此时间复杂度取决于解的个数。假设候选数组的长度为n，目标值为target，最坏情况下解的个数为O(2^n)。
• 在每个解中，我们需要遍历当前候选数组的剩余部分，因此在每个递归层级中，时间复杂度为O(n-i)，其中i为当前层级的起始位置。

综上所述，整体的时间复杂度为O(2^n * n)。

空间复杂度：

• 回溯算法使用了额外的空间来存储当前路径和结果集，因此空间复杂度取决于解的个数和每个解的平均长度。
• 结果集的空间复杂度为O(2^n * avg_len)，其中avg_len是每个解的平均长度。
• 当前路径的空间复杂度为O(n)。
• 综上所述，整体的空间复杂度为O(2^n * avg_len + n)。

（avg_len无法确定）

注意点

1. 对循环的剪枝：如果 sum + candidates[i] > target 就终止遍历

代码实现

剪枝：如果 sum + candidates[i] > target 就终止遍历

class Solution {
private: 
    vector<int> path;
    vector<vector<int>> result;
    int sum = 0;
public:
    void backtracking(vector<int>& candidates,int target,int begin){
        if(sum == target) result.push_back(path);
        else if(sum > target) return;
		
        // 剪枝：如果 sum + candidates[i] > target 就终止遍历
        for(int i = begin;i < candidates.size() && sum + candidates[i] <= target;i++){
            path.push_back(candidates[i]);
            sum += candidates[i];
            backtracking(candidates,target,i); // 注意，传递的是i不是begin
            path.pop_back();
            sum -= candidates[i];
        }

    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates,target,0);
        return result;
    }
};

---

组合总和Ⅱ

思路

重点是去重。

首先把原数组排序，用used数组标记是否使用过。

若当前元素与上一元素相等，如果used[i-1]为true，说明是树枝部分重复，可以继续；如果used[i-1]为false，说明在树层部分重复，需要跳过，去重。

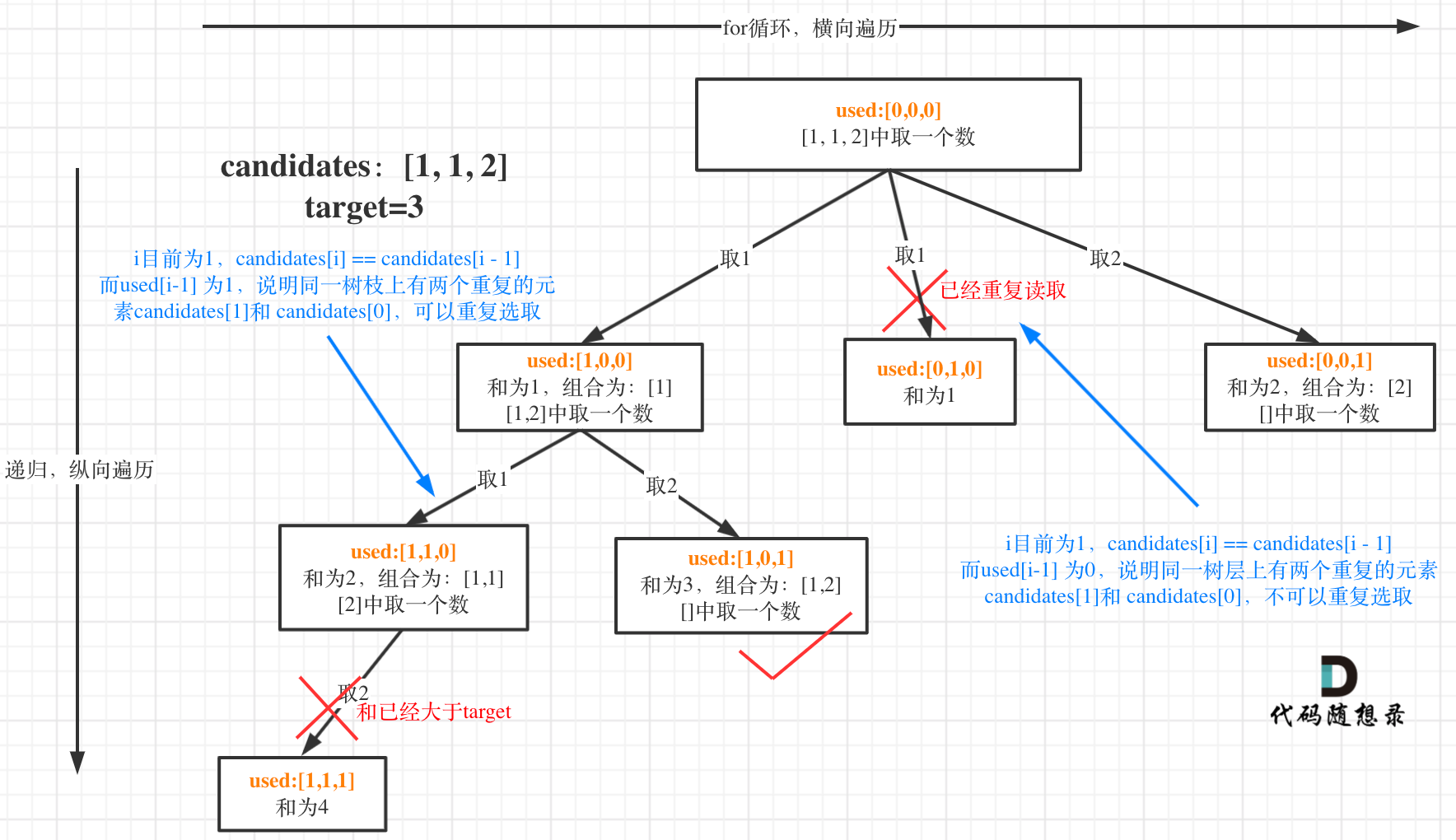
复杂度分析

时间复杂度：

• 在最坏情况下，回溯算法会遍历所有可能的组合。假设候选数组的长度为n，目标值为target，那么最坏情况下，解的个数为O(2^n)。
• 在每个解中，我们需要遍历当前候选数组的剩余部分，因此在每个递归层级中，时间复杂度为O(n-i)，其中i为当前层级的起始位置。
• 综上所述，整体的时间复杂度为O(2^n * n)。

空间复杂度：

• 回溯算法使用了额外的空间来存储当前路径和结果集，因此空间复杂度取决于解的个数和每个解的平均长度。
• 结果集的空间复杂度为O(2^n * avg_len)，其中avg_len是每个解的平均长度。
• 当前路径的空间复杂度为O(n)。
• 综上所述，整体的空间复杂度为O(2^n * avg_len + n)。

注意点

1. 去重的要素：数组有序、相邻两个元素是否相等、used数组标记是否使用过。

   不要忘记先排序！

代码实现

class Solution {
private:
    vector<int> path;
    vector<vector<int>> result;

public:
    void backtracking(vector<int>& candidates,int target,vector<bool> used,int begin,int sum){
        if(sum == target){
            result.push_back(path);
            return;
        }else if(sum > target) return;

        for(int i = begin;i < candidates.size() && sum < target;i++){
            // 去重
            // 第一个==表示相邻两个元素值相等；
            // 第二个==表示上一个元素已经使用过
            // 只有上一个元素使用过，且当前元素值等于上一元素时，跳过，树层去重
            if(i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false) continue;
            path.push_back(candidates[i]);
            sum += candidates[i];
            used[i] = true;
            backtracking(candidates,target,used,i+1,sum);
            path.pop_back();
            sum -= candidates[i];
            used[i] = false;
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(),false);
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,used,0,0);
        return result;
    }
};

不使用used数组：

    class Solution {
    private:
        vector<int> path;
        vector<vector<int>> result;

    public:
        void backtracking(vector<int>& candidates,int target,int begin,int sum){
            if(sum == target){
                result.push_back(path);
                return;
            }else if(sum > target) return;

            for(int i = begin;i < candidates.size() && sum < target;i++){
                // 跳过同一树层使用过的元素
                if(i > begin && candidates[i - 1] == candidates[i]) continue;
                path.push_back(candidates[i]);
                sum += candidates[i];
                backtracking(candidates,target,i+1,sum);
                path.pop_back();
                sum -= candidates[i];
            }
        }

        vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
            vector<bool> used(candidates.size(),false);
            sort(candidates.begin(),candidates.end());
            backtracking(candidates,target,0,0);
            return result;
        }
    };

---

分割回文串

leetcode:131. 分割回文串

回溯法

思路

基础可以看作是不重复使用的组合问题。每次在子串中分割，分隔符就是begin这个下标。子串就是begin~i这个范围。

复杂度分析

时间复杂度：O(n * 2^n)。

空间复杂度：O(n^2)。

注意点

1. 回文判断别写错，if(s[i] != s[j]) return false;。

代码实现

class Solution {
private:
    vector<vector<string>> result;
    vector<string> path;
public:
    void backtracking(string& s,int begin){
        if(begin >= s.size()){
            result.push_back(path);
            return;
        }
        
        for(int i = begin;i < s.size();i++){
            if(isPalindrome(s,begin,i)){
                path.push_back(s.substr(begin,i - begin + 1));
                backtracking(s,i+1);
                path.pop_back();
            }
        }
    }

    // 左闭右闭
    bool isPalindrome(string& s,int begin,int end){
        for(int i = begin,j = end;i < j;i++,j--){
            if(s[i] != s[j]) return false;
        }
        return true;
    }

    vector<vector<string>> partition(string s) {
        backtracking(s,0);
        return result;
    }
};