深度学习基础认知小抄

前言

该内容为基于博主对深度学习的认知与实践经验的对李宏毅油管上课程的简要理解，有局限偏差之处，敬请谅解。后续随着学习的深入会进行一定修正。

本质概述

此处不会特意探讨机器学习与深度学习之间的差别，纵观这些领域，它们所构建的方法论为：寻找到一个模型（函数），人们期望输入为x，输出为y。

为了解决相对复杂的问题，通常模型（函数）是十分复杂的，其表现在具有多个未知的参数。在深度学习中，人们为构建这样一个模型，一般情况下，会使用已有的数据资料来对随机初始化的模型进行训练，训练结束后会获取到一个改变了参数的模型，该模型可以达成期望输入为x，输出为y的目的。

在训练过程中，对模型输入已有的输入数据x，模型输出数据y'，y'与已有的输出数据y在训练阶段会存在差异，它们之间的差异（误差）通过设定的损失函数（Loss）来衡量，对这样的误差进行梯度计算，反馈给模型进行内部参数的修改，这样的过程算法为梯度下降算法。

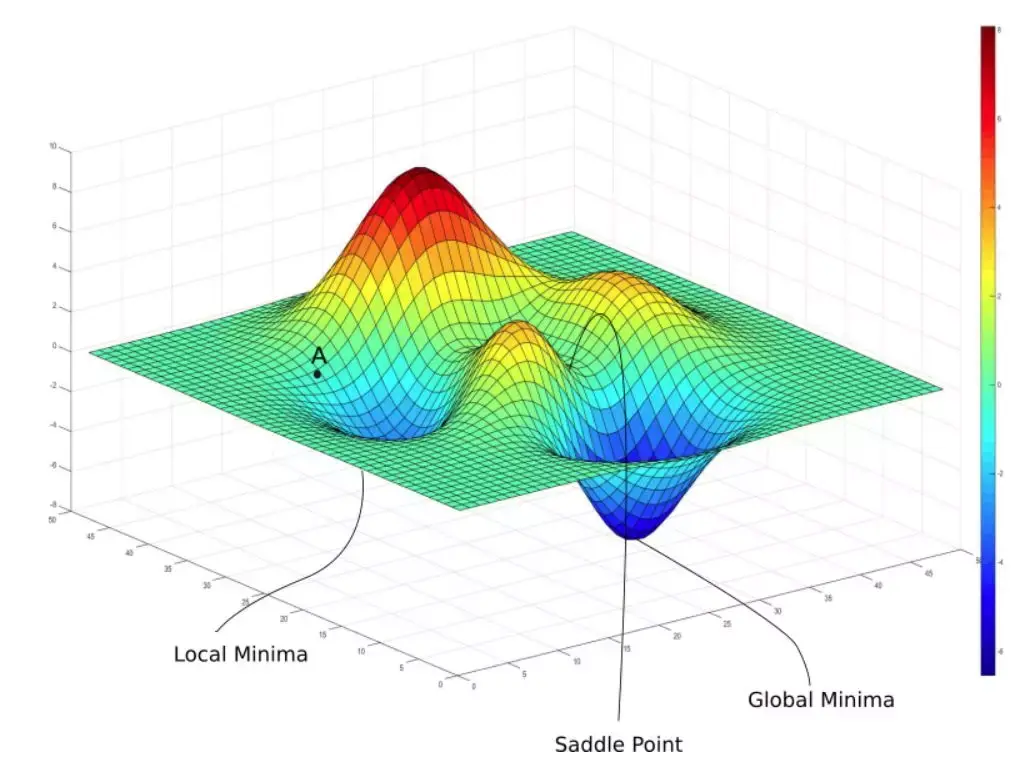
随着梯度下降算法的运行，模型会逐渐的拟合为人们期望的状态。这样拟合的过程为便于理解可以将其可视化为error surface。

形象的是，模型训练的正常运行代表着在图中模型生成的误差点会滚落到图中的低点直到loss趋于稳定不再下降。图中这些低点也称为cirtical point，在这些点上梯度为0，包含了局部最小点（Local Minima），全局最小点（Global Minima），鞍点（Saddle Point,周边梯度有正有负）。不考虑训练集与测试集的数据差异，模型训练应该掉落到全局最小点为佳。

模型构建——一个简单的例子

构建一个简单的模型y=wx+b,该模型函数为线性函数，为了让模型能拟合非线性函数，模型变化为y=A(wx+b)，其中A()为激活函数（Active Function）。目前提出了众多的激活函数如Sigmoid，ReLu等，工程上前沿论文多采用ReLu（博主猜测是一种经验论并且效果确实不错）。
在深度学习中，y=A(wx+b)的输出又可以作为输入再次套入新的函数中如y'=A(w'x+b')。因此通过这样的方式构建出具有众多参数的复杂模型，y=A(wx+b)可以作为模型中的一层（layer）。

模型训练的要点——观察loss的表现

在一般向的深度学习流程中，假设以全监督训练为前提，人们拥有一定数量的已知数据（包含输入与输出），通过将数据用于对设计模型的训练，获取得到一个目标模型。对该目标模型的期望为，输入未知输出的输入数据，模型输出的内容与目标相匹配。

因此在其中就产生了训练集与测试集，测试集往往是未知的。而模型输入数据得到输出的过程可以获取loss值，因而模型的训练根据loss的表现可以分成多种情况。

训练集loss很大-模型简单

如果模型过于简单，那么模型就无法对复杂的任务目标进行拟合，因此要考虑设计复杂的模型（多加几层...）。

训练集loss很大-优化不好

这种情况往往是训练过程中loss梯度下降跑到了局部最小点或者是鞍点，无法下降到更低，为此在训练中有各种办法尝试去解决这个问题。

---

关于局部最小与鞍点

很多时候模型训练很难达到最理想的情况，模型最终陷入局部最小点或鞍点。可以通过数学公式计算判断模型是陷入到局部最小或鞍点，详细计算与鞍点的解决办法看关于局部最下与鞍点的计算-关联到线代知识。但其实在pytorch的代码运行上博主暂时还没看到特意去解决这个问题的例子。

关于动量与学习率

动量和学习率直接关联到模型能否逃离局部最小或鞍点。动量类似物理学上的概念，当梯度趋于平缓时动量的累积可以让模型逃离。而学习率因为是和梯度相乘，直接关联到了梯度的改变，过大可能会造成在“山谷”区域的来回震荡，过小也不利于逃离。

在学习率上，相关工作提出了Adaptive Learning rate，AdaGrad对学习率除以以往梯度的二次平均开根号来让学习率自适应。如果以往梯度较大，学习率会变小，以往梯度较小，学习率会变大。

对AdaGrad进一步优化为RMSProp，对学习率除以上一次分母与该次梯度的二次开根号，上一次分母与该次梯度通过一个权重超参数进行影响因素的控制。这样子使得能对学习率进一步的控制。

在此基础上Adam结合了动量与RMSProp。目前Adam在训练上运用的最为广泛表现相对稳定。但在一些工程实践上，SGD也有较多的情况在测试集上表现更为优秀。

本身学习率自身也可以通过简单的step关联的计算进行改变（Learning Rate Decay），一种是随着训练学习率逐渐变小，另一种是warm up，及先变大后变小（比较经验论）。

关于Batch

基于GPU平行计算的前提下。合适数量的大Batch与小Batch在单Batch的计算时间上差不多，但是对于整个epoch的计算大Batch速度明显更快。
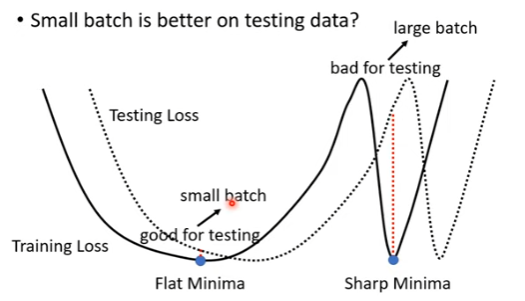
而就结果而言，小Batch可能有着更好的结果，一种解释在于大Batch的梯度下降可能更为激进。这导致了小batch容易陷入宽阔的局部最小点（flat local minima）,大batch容易陷入狭窄的局部最小点（sharp local minima）。在训练集与测试集一定会有偏差的前提下，测试集的可视化会整体偏移。而陷入平缓局部最小点的模型更能抵抗偏移带来的改变。

关于损失函数

损失函数的不同将会决定整个error surface的不同，合理的分布有助于梯度下降。

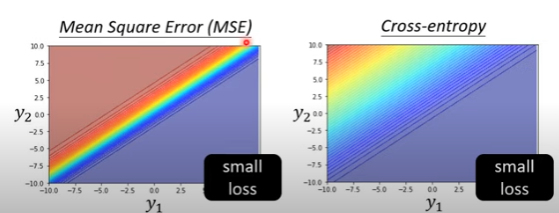
图中交叉熵损失函数和MSE作对比，MSE的分布就不是很合理，假如从左上角改变到右下角，MSE的梯度下降会更为困难。经验上的，采用交叉熵损失函数（cross-entroy）去训练模型居多。

关于Normalization

在各个层面进行normalization起到不同的作用。

• Feature Norm

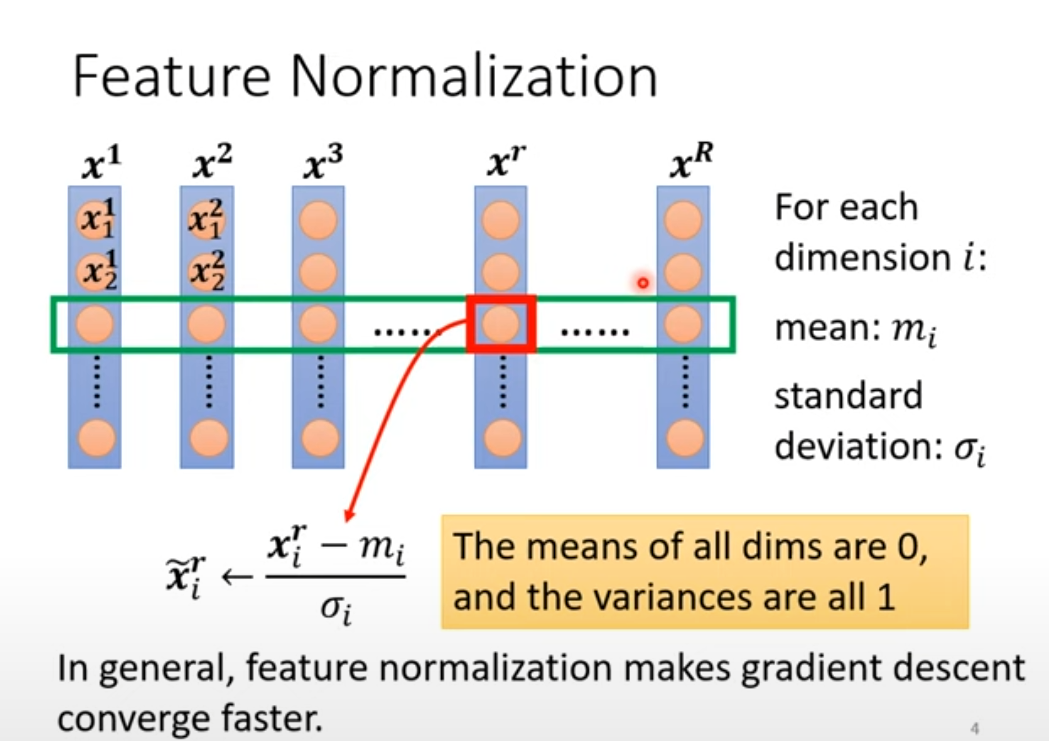
Feature Normalization用于改变error surface，使得每个数据维度对训练结果造成的影响不受到数据大小的影响，让训练更容易。

• Batch Norm

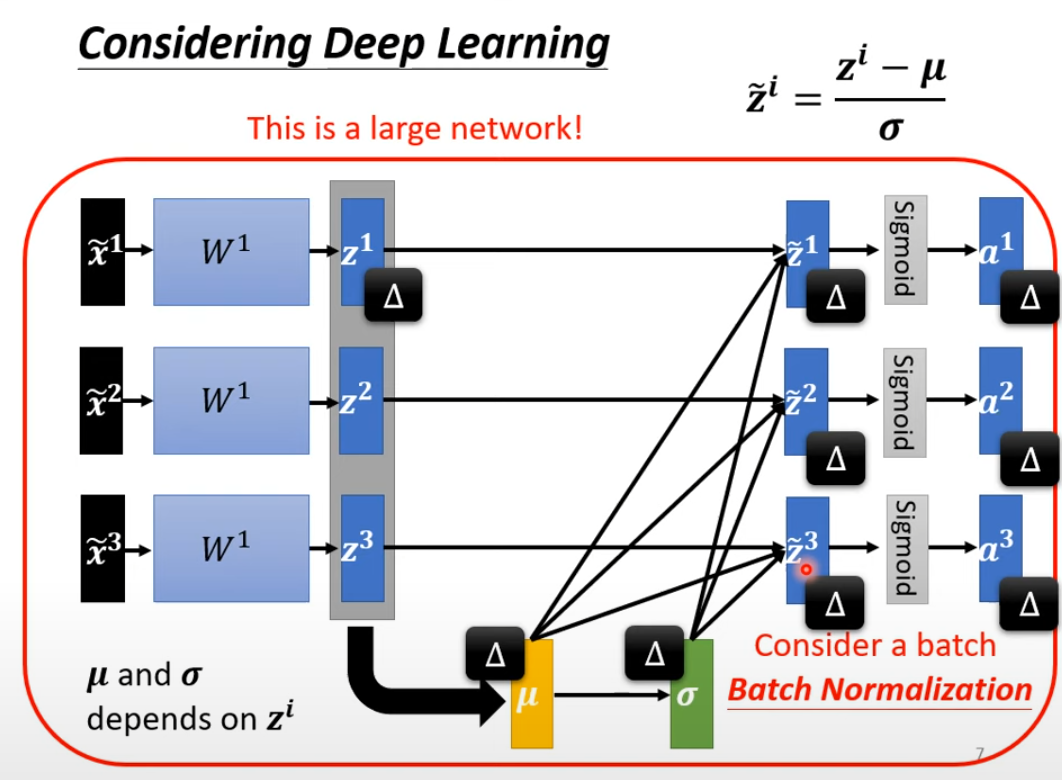
BN可以在激活函数前，也可以在激活函数后。

多加了两个超参数是觉得BN的特性（平均为0，方差为1）对网络造成了限制，可能会对训练结果带来负面影响，干脆让模型自己调整学习。

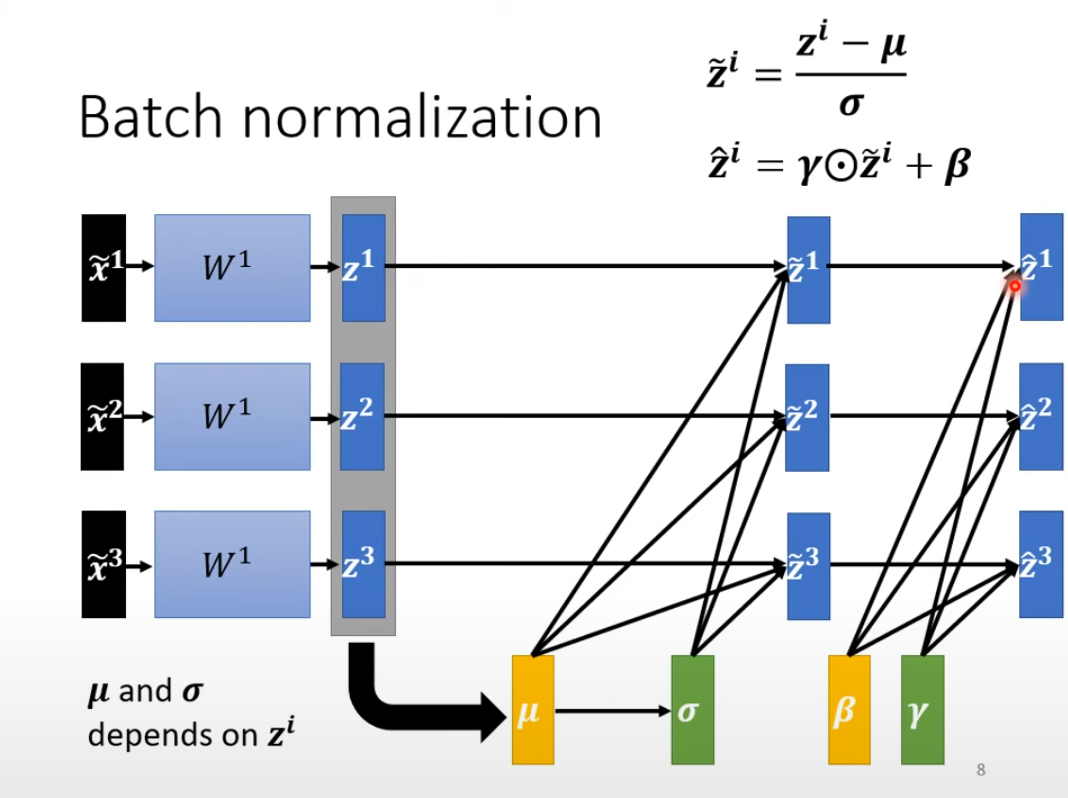
BN在训练过程中经过验证表现不错，但它的发现其实是随缘的，不是发明出来的比较玄学...

---

训练集loss很小，测试集loss很大-模型复杂或是数据集不匹配

过于复杂的模型很容易造成过拟合（overfitting），相当于模型只对训练集的内容拟合正确，但太过复杂也会导致测试集内容偏差过大。

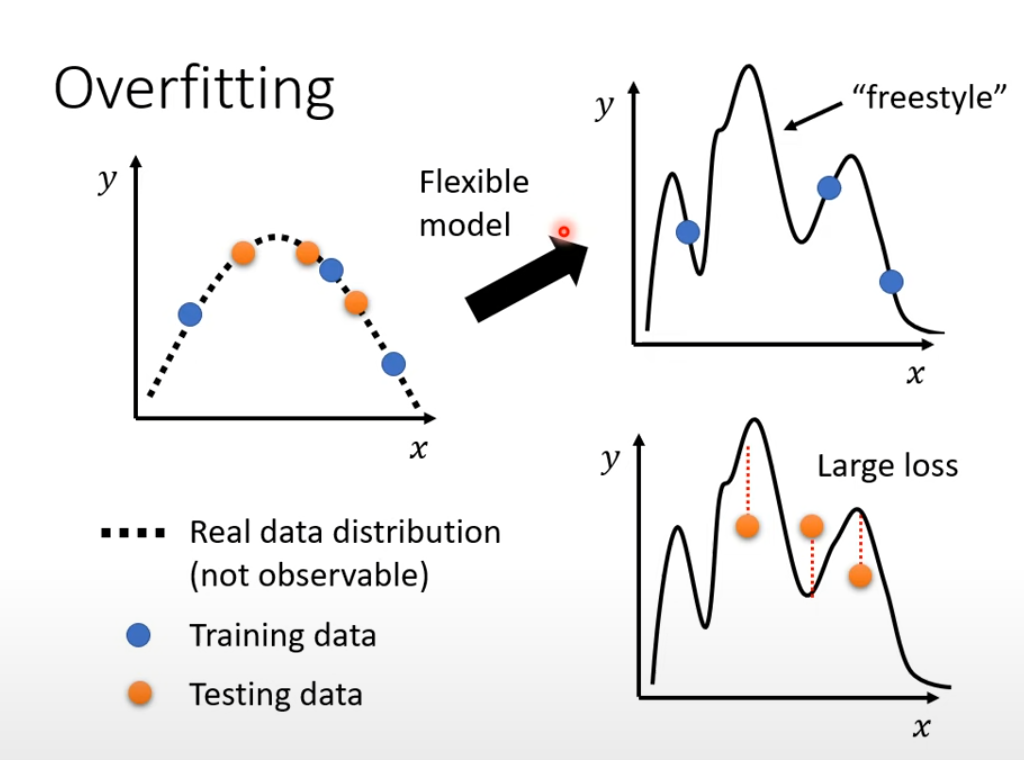
直观的做法是在实际实验过程中应该先去尝试一些简单模型，如果简单模型的训练效果好那么就可以判断之前训练的模型较为复杂了，可以尝试去简化模型。

另一种做法是对训练集做数据增强，通过合理的增加训练集数据数量使得拟合曲线尽可能的接近实际曲线。当然这涉及到了一个重要的考虑因素-训练集与测试集之间的差异。这个考虑因素也极有可能是造成了训练集loss很小，测试集loss很大的原因。

在其余条件理想的训练情况下，模型反应的是在训练集的数据分布上的规律。如果训练集与测试集之间差异过大的话，就可能会出现在训练集上表现良好，但在测试集上表现不佳的情况。由此在对训练集的处理上（数据清洗，数据增强等）需要去花心思避免训练集与测试集差异过大。

当然在正常情况下原始的训练集与测试集之间不会差异太大。为了在仅有训练集的情况下得到最优秀的模型，训练集中的一部分需要划分出来作为验证集，这样的做法可以缓解数据集不匹配的情况。划分方法可以是单一划分出一个固定的验证集，也可以是将数据集划分多份，每一份作为一次验证集（n-fold），模型也要训练多次取平均的指标用于衡量模型好坏。

参考

- [1] 李宏毅机器学习2021