线段树、Trie和并查集01：线段树

对于有一类问题，我们关心的是一个线段（区间），比如区间染色、区间查询

对于一个给定的区间，更新区间中一个元素的值或者查询区间中的最大最小值或者总和，使用线段树更快，又称区间树

线段树是一种平衡二叉树（最大深度和最小深度差值<=1，堆也是平衡二叉树），其节点存储的是一个区间的信息，比如该区间的总和，根节点存储整个区间的总和，依次往下区间一分为二，叶子节点存储的是只有一个元素的区间和，也就是单个元素本身

操作（不考虑增删）	数组实现	线段树实现
区间更新	O(n)	O(logn)
区间查询	O(n)	O(logn)

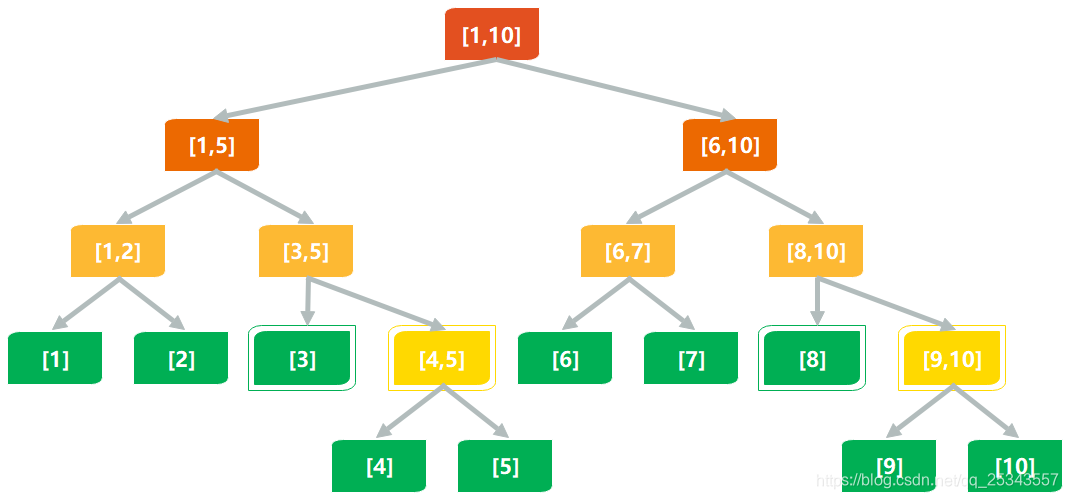
数组实现线段树

线段树不一定是满二叉树，但是可以将其看作是满二叉树，最后一层空的地方保留

因此，对于有n个元素的区间，如果n刚好为2的整数幂次方，那节点数为2n；如果不是，那最后一层肯定不满，而最后一层的节点数等于前面所有的节点数，因此需要开辟4n个节点的空间

综上，对于n个元素需要开辟大小为4n的数组来存储线段树

public class Algorithm {

    public static void main(String[] args) {

        Integer[] arr = {-2, 0, 3, -5, 2, -1};
        SegmentTree<Integer> segmentTree = new SegmentTree<>(arr, new Merger<Integer>() {

            @Override
            public Integer merge(Integer a, Integer b) {
                return a + b;
            }
        });

        System.out.println(segmentTree);
        System.out.println(segmentTree.query(0, 2));
        segmentTree.set(arr.length - 1, 0);
        System.out.println(segmentTree);

        /**
         * 在创建对象时使用匿名内部类和lambda表达式，需要满足以下条件：
         * 必须是一个接口
         * 接口只能有一个方法
         */
//        SegmentTree<Integer> segmentTree = new SegmentTree<>(arr, (a, b) -> a + b);
    }
}

/**
 * 静态数组实现线段树
 * 线段树只考虑改查，不考虑增删元素，故不需要使用动态数组
 */
class SegmentTree<E> {

    /**
     * 定义两个数组，一个存放原始数组，大小为n；一个存放转换后的线段树，大小为4n
     * 传入自定义的Merger操作
     */
    E[] data;
    E[] tree;
    Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger){

        data = (E[]) new Object[arr.length];
        tree = (E[]) new Object[arr.length * 4];
        this.merger = merger;

        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }

        /**
         * 在构造函数将数组转换为线段树
         */
        buildSegmentTree(0, 0, data.length - 1);
    }

    public int getSize(){

        return data.length;
    }

    public E get(int index){

        if (index < 0 || index >= data.length){
            throw new IllegalArgumentException("索引值非法");
        }

        return data[index];
    }

    public int leftChild(int index){

        return index * 2 + 1;
    }

    public int rightChild(int index){

        return index * 2 + 2;
    }

    /**
     * 创建线段树
     * 计算区间[left, right]的和，将值保存在节点索引为treeIndex的线段树中，初始为0，存放的是整个数组区间的和
     * 如果区间长度为1那就返回这一个值，否则将区间一分为二，分别进行递归，子树的和分别存放在左右孩子中，而根节点就是左右孩子相加
     */
    public void buildSegmentTree(int treeIndex, int left, int right){

        if (left == right){

            tree[treeIndex] = data[left];

            return;
        }

        int mid = left + (right - left) / 2;

        buildSegmentTree(leftChild(treeIndex), left, mid);
        buildSegmentTree(rightChild(treeIndex), mid + 1, right);

        /**
         * 可以自定义对区间进行的操作，定义一个新的接口Merger来实现不同的功能，比如区间求和，区间取最大值
         * 泛型是不能直接相加的，想要进行比较就要实现Camparable接口，想要进行其他操作就要定义一个接口去实现
         */
        tree[treeIndex] = merger.merge(tree[leftChild(treeIndex)], tree[rightChild(treeIndex)]);
    }

    /**
     * 修改节点
     * 先修改原数组的值，再修改线段树
     * 先找到要修改的节点，当区间长度为1时说明找到了，否则判断这个节点在左右哪棵子树，递归查找
     * 查找并修改该节点以后，将最新的结果返回给父节点，最终完成所有区间的更新
     */
    public void set(int index, E value){

        if (index < 0 || index >= data.length){
            throw new IllegalArgumentException("索引值非法");
        }

        data[index] = value;
        set(0, 0, data.length - 1, index, value);
    }

    private void set(int treeIndex, int left, int right, int index, E value){

        if (left == right){

            tree[treeIndex] = value;
            return;
        }

        int mid = left + (right - left) / 2;

        if (index >= mid + 1){
            set(rightChild(treeIndex), mid + 1, right, index, value);
        }
        else {
            set(leftChild(treeIndex), left, mid, index, value);
        }

        tree[treeIndex] = merger.merge(tree[leftChild(treeIndex)], tree[rightChild(treeIndex)]);
    }

    /**
     * 查询[queryLeft, queryRight]区间范围的和
     */
    public E query(int queryLeft, int queryRight){

        if (queryLeft < 0 || queryRight < 0 || queryLeft >= data.length || queryRight >= data.length || queryLeft > queryRight){
            throw new IllegalArgumentException("索引值非法");
        }

        return query(0, 0, data.length - 1, queryLeft, queryRight);
    }

    /**
     * 在根节点为treeIndex的线段树的[left, right]区间中，寻找[queryLeft， queryRight]区间范围的和
     * 如果这个区间完全在某一颗子树，那就不用考虑另外一颗子树；否则要将区间拆分开来，分别计算和再相加
     */
    private E query(int treeIndex, int left, int right, int queryLeft, int queryRight){

        if (queryLeft == left && queryRight == right){

            return tree[treeIndex];
        }

        int mid = left + (right - left) / 2;

        if (queryLeft >= mid + 1){

            return query(rightChild(treeIndex), mid + 1, right, queryLeft, queryRight);
        }
        else if (queryRight <= mid){

            return query(leftChild(treeIndex), left, mid, queryLeft, queryRight);
        }
        else {

            /**
             * 此时要查找的区间边界发生了改变
             */
            E resLeft = query(leftChild(treeIndex), left, mid, queryLeft, mid);
            E resRight = query(rightChild(treeIndex), mid + 1, right, mid + 1, queryRight);

            return merger.merge(resLeft, resRight);
        }
    }

    @Override
    public String toString(){

        StringBuilder str = new StringBuilder();

        str.append("[");

        for (int i = 0; i < tree.length; i++) {

            str.append(tree[i]);

            if (i != tree.length - 1){
                str.append(", ");
            }
        }

        str.append("]");

        return str.toString();
    }
}

/**
 * 创建一个接口Merger，用来定义对两个泛型元素进行的操作
 */
interface Merger<E>{

    E merge(E a , E b);
}

复杂度分析

线段树的set()和query()方法的时间复杂度为O(logn)