二分搜索树01:实现二分搜索树
常用树结构
- 二分搜索树
- 平衡二分搜索树(AVL)、红黑树
- 堆;并查集
- 线段树;Trie(字典树、前缀树)
二叉树基础
和链表一样,二叉树是一种动态数据结构,数据存储在“节点”(Node)中,left指针指向左孩子,right指针指向右孩子
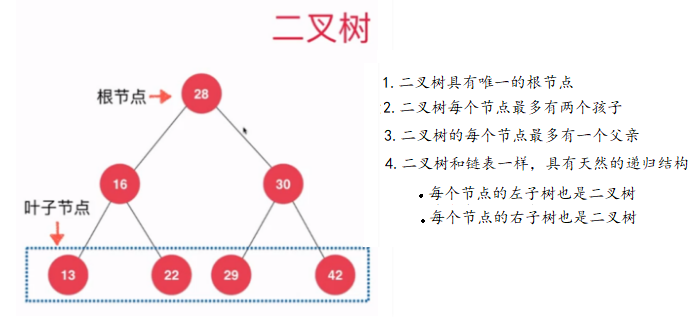
二叉树具有唯一根节点,每个节点最多有两个孩子,没有孩子的节点称为叶子节点
二叉树具有天然的递归结构,每个节点的左右子树也是二叉树
二分搜索树基础
二分搜索树是二叉树,其每个子树也是二分搜索树
二分搜索树的节点值满足以下条件:大于左子树的任意节点值,小于右子树的任意节点值,不能重复
也就是根节点相当于二分查找法中的mid,只需比较target和根节点的大小,就可以快速的判断出其在左子树还是右子树,然后用递归的方式直到查找到目标

递归实现二分搜索树
增、删、改、查,前序、中序、后序遍历
public class Algorithm {
public static void main(String[] args) {
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
int[] nums = {5,3,6,8,4,2};
for (int i : nums) {
bst.add(i);
}
bst.preOrder();
System.out.println();
bst.inOrder();
System.out.println();
bst.postOrder();
System.out.println();
System.out.println(bst.removeMin());
System.out.println();
System.out.println(bst.removeMax());
System.out.println();
bst.remove(5);
System.out.println();
bst.preOrder();
}
}
class BinarySearchTree<E extends Comparable<E>> {
/**
* 通过节点类Node实现二分搜索树
*/
private class Node{
public E e;
public Node leftNext;
public Node rightNext;
private Node(E e){
this.e = e;
leftNext = null;
rightNext = null;
}
}
private Node root;
private int size;
public BinarySearchTree(){
root = null;
size = 0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
/**
* 增
* 从根节点挨个进行递归比较,值相同则抛弃,不同则判断往左还是往右,当某个节点左右孩子为空时则添加
* 最后一定要返回新树的根节点,否则不能链接到新的树
*/
public void add(E e) {
root = add(root, e);
}
private Node add(Node root, E e){
if (root == null){
size++;
return new Node(e);
}
if (root.e.compareTo(e) < 0){
root.rightNext = add(root.rightNext, e);
}
else if (root.e.compareTo(e) > 0) {
root.leftNext = add(root.leftNext, e);
}
return root;
}
/**
* 删(Hubbard Deletion)
* 先找到待删除节点,如果该节点有左右孩子,那就让右子树的最小节点或者左子树的最大节点顶替该节点的位置
* 先获取右子树的最小节点,其就是新的根节点,让其指向待删除节点的左右孩子,注意右孩子是删除最小节点后新的右孩子,最后安全删除节点,返回新的根节点
* 注意不能把最大/小节点值直接赋值给该节点,因为其可能也有左右子树
*/
public void remove(E e){
root = remove(root, e);
}
private Node remove(Node root, E e){
if (root == null){
return null;
}
if (root.e.compareTo(e) < 0){
root.rightNext = remove(root.rightNext, e);
return root;
}
else if (root.e.compareTo(e) > 0){
root.leftNext = remove(root.leftNext, e);
return root;
}
else {
if (root.leftNext == null) {
Node newRoot = root.rightNext;
root.rightNext = null;
size--;
return newRoot;
} else if (root.rightNext == null) {
Node newRoot = root.leftNext;
root.leftNext = null;
size--;
return newRoot;
} else {
/**
* removeMin()方法中已经进行过size--
*/
Node newRoot = Min(root.rightNext);
newRoot.rightNext = removeMin(root.rightNext);
newRoot.leftNext = root.leftNext;
root.leftNext = null;
root.rightNext = null;
return newRoot;
}
}
}
/**
* 删除最小的节点
* Min()方法在树为空时已经做出判断了,故无需再次判断
* 传入根节点进行递归查找,如果左孩子为空,说明该节点就是最小节点
* 删除最小节点以后新的根节点就是右孩子,最后返回新的根节点
*/
public E removeMin(){
E value = Min();
root = removeMin(root);
return value;
}
private Node removeMin(Node root){
if (root.leftNext == null){
Node newRoot = root.rightNext;
root.rightNext = null;
size--;
return newRoot;
}
root.leftNext = removeMin(root.leftNext);
return root;
}
/**
* 删除最大的节点
*/
public E removeMax(){
E value = Max();
root = removeMax(root);
return value;
}
private Node removeMax(Node root){
if (root.rightNext == null){
Node newRoot = root.leftNext;
root.leftNext = null;
size--;
return newRoot;
}
root.rightNext = removeMax(root.rightNext);
return root;
}
/**
* 改
* 前序遍历,先访问根节点,再递归访问左子树和右子树
*/
public void preOrder(){
preOrder(root);
}
private void preOrder(Node root){
if (root == null) {
return;
}
System.out.println(root.e);
preOrder(root.leftNext);
preOrder(root.rightNext);
}
/**
* 中序遍历,先递归访问左子树,再访问根节点,最后递归访问右子树
* 该结果就是所有节点的升序排列
*/
public void inOrder(){
inOrder(root);
}
private void inOrder(Node root){
if (root == null){
return;
}
inOrder(root.leftNext);
System.out.println(root.e);
inOrder(root.rightNext);
}
/**
* 后序遍历,先递归访问左子树,再递归访问右子树,最后访问根节点
*/
public void postOrder(){
postOrder(root);
}
private void postOrder(Node root){
if (root == null){
return;
}
postOrder(root.leftNext);
postOrder(root.rightNext);
System.out.println(root.e);
}
/**
* 查
*/
public boolean contains(E e){
return contains(root, e);
}
private boolean contains(Node root, E e){
if (root == null) {
return false;
}
if (root.e.compareTo(e) == 0){
return true;
}
else if (root.e.compareTo(e) > 0){
return contains(root.leftNext, e);
}
else {
return contains(root.rightNext, e);
}
}
/**
* 查找最小的节点
* 如果左孩子为空,则当前节点就是最小节点
*/
public E Min(){
return Min(root).e;
}
private Node Min(Node root){
if (root == null){
return null;
}
if (root.leftNext == null){
return root;
}
return Min(root.leftNext);
}
/**
* 查找最大的节点
*/
public E Max(){
return Max(root).e;
}
private Node Max(Node root){
if (root == null){
return null;
}
if (root.rightNext == null){
return root;
}
return Max(root.rightNext);
}
@Override
public String toString(){
StringBuilder str = new StringBuilder();
generateString(root, 0, str);
return str.toString();
}
public void generateString(Node root, int depth, StringBuilder str){
if (root == null) {
str.append(generateDepth(depth) + "null\n");
return;
}
str.append(generateDepth(depth) + root.e + "\n");
generateString(root.leftNext, depth + 1, str);
generateString(root.rightNext, depth + 1, str);
}
public String generateDepth(int depth){
StringBuilder str = new StringBuilder();
for (int i = 0; i < depth; i++) {
str.append("--");
}
return str.toString();
}
}
深入理解前中后序遍历(深度优先遍历DFS)
前中后指的是访问根节点的顺序,前序遍历第一次遇到该节点就打印,中序遍历第二次遇见该节点才打印,后序遍历则是第三次遇见该节点才打印
栈其实就是递归的一种实现结构,因此前中后序遍历都可以借助栈使用非递归的方式来实现
中序遍历的应用:中序遍历相当于排序,可以打印出按顺序排列的所有节点
后序遍历的应用:为二分搜索树释放内存,只有先释放了子树,才能释放根节点
拓展:使用栈实现前序遍历的非递归写法
public void preOrder(){
preOrder(root);
}
public void preOrder(Node root) {
/**
* 前序遍历,在每次弹出节点后,先后压入自己的右孩子和左孩子
* 然后对栈顶节点,也就是左孩子执行相同的操作,直到所有的左子树都遍历完了,再遍历右子树
* 栈空了说明所有节点都遍历并且弹出了
*/
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null) {
stack.push(cur.right);
}
if (cur.left != null) {
stack.push(cur.left);
}
}
}
中序遍历和后序遍历的非递归实现更复杂,实际应用也不广
层序遍历(广度优先遍历BFS)
根节点为第0层
因为需要先进先出才能一层一层的来遍历二叉树,因此广度优先遍历可以借助队列使用非递归方式来实现
public void levelOrder(){
levelOrder(root);
}
public void levelOrder(Node root) {
/**
* 层序遍历,每次节点出队后,先后将自己的左右孩子入队
* 然后对队首节点,也就是左孩子执行相同的操作,再让左孩子的左右孩子入队
* 每次循环记录下当前层的元素个数,全部出队以后剩下的都是下一层的
* 队列空了说明所有节点都遍历并且出队了
*/
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
int sameLevelNum = queue.size();
for (int i = 0; i < sameLevelNum; i++) {
TreeNode node = queue.poll();
System.out.println(node.e);
if (node.left != null){
queue.add(node.left);
}
if (node.right != null){
queue.add(node.right);
}
}
}
}
常用于算法设计中——最短路径




 浙公网安备 33010602011771号
浙公网安备 33010602011771号