动态数据结构基础02:链表和递归
递归的思路
public class Algorithm {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8};
System.out.println(sum(arr));
}
public static int sum(int[] arr){
return sum(arr, 0);
}
/**
* 递归的宏观语意
* 计算arr[start, arr.length - 1]的和
*/
public static int sum(int[] arr, int start){
/**
* 1、求解最基本的问题
*/
if (start == arr.length){
return 0;
}
/**
* 2、把原问题转换为更小的问题
*/
return arr[start] + sum(arr, start + 1);
}
}
递归调用是有代价的:方法调用+系统栈空间
链表天然的递归性
近乎和链表相关的所有操作,增、删、改、查都可以用递归实现
public class Algorithm {
public static void main(String[] args) {
LinkedList<Integer> linkedList = new LinkedList<>();
for (int i = 0; i < 5; i++) {
linkedList.addFirst(i);
System.out.println(linkedList);
}
linkedList.add(666, 3);
linkedList.remove(1);
System.out.println(linkedList);
System.out.println(linkedList.contains(0));
System.out.println(linkedList.contains(4));
linkedList.set(888, 4);
System.out.println(linkedList);
System.out.println(linkedList.get(4));
}
}
class LinkedList<E>{
private class Node{
public E e;
public Node next;
public Node(E e, Node next){
this.e = e;
this.next = next;
}
public Node(){
this.next = null;
}
}
private Node dummyHead;
private int size;
public LinkedList(){
dummyHead = new Node(null, null);
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
public Node getPrevNode(int index){
/**
* 除了add()方法,其他方法都不可以取到size,因此在那些方法里需要单独判断index == size
*/
if (index < 0 || index > size){
throw new IllegalArgumentException("索引值非法");
}
/**
* 递归终止条件
*/
if (index == 0){
return dummyHead;
}
/**
* 查找index的前一个节点,可以先查找index - 1的前一个节点prev,然后这个节点的下一个节点就是目标节点
*/
Node prev = getPrevNode(index - 1);
return prev.next;
}
public void add(E e, int index) {
Node prev = getPrevNode(index);
prev.next = new Node(e, prev.next);
size++;
}
public void addFirst(E e){
add(e, 0);
}
public void addLast(E e){
add(e, size);
}
public E remove(int index){
/**
* 单独判断index == size
*/
if (index == size){
throw new IllegalArgumentException("索引值非法");
}
Node prev = getPrevNode(index);
Node tem = prev.next;
prev.next = tem.next;
tem.next = null;
size--;
return tem.e;
}
public E removeFirst(){
return remove(0);
}
public E removeLast(){
return remove(size - 1);
}
public void set(E e, int index){
if (index == size){
throw new IllegalArgumentException("索引值非法");
}
Node prev = getPrevNode(index);
prev.next.e = e;
}
public E get(int index){
if (index == size){
throw new IllegalArgumentException("索引值非法");
}
Node prev = getPrevNode(index);
return prev.next.e;
}
public E getFirst(){
return get(0);
}
public E getLast(){
return get(size - 1);
}
public boolean contains(E e){
for (Node prev = dummyHead; prev.next != null; prev = prev.next){
if (prev.next.e.equals(e)){
return true;
}
}
return false;
}
@Override
public String toString(){
StringBuilder str = new StringBuilder();
Node prev = dummyHead;
System.out.println("链表元素个数为:" + getSize());
while (prev.next != null){
str.append(prev.next.e + "——>");
prev = prev.next;
}
str.append("null");
return str.toString();
}
}
作业:利用辅助方法打印递归的详细过程
public class Algorithm {
public static void main(String[] args) {
int[] arr = {1, 2, 6, 3, 4, 5, 6};
ListNode head = new ListNode(arr);
System.out.println(head);
System.out.println(new Solution().removeElements(head, 6, 1));
}
}
class Solution {
public ListNode removeElements(ListNode head, int val, int depth) {
/**
* 每次执行removeElements()方法之前打印当前的深度,还有当前链表的头节点
*/
String depthScale = depth(depth);
System.out.print(depthScale);
System.out.println("Call:Remove " + val + " in " + head);
/**
* 递归终止条件
*/
if (head == null){
System.out.print(depthScale);
System.out.println("Return:" + head);
return head;
}
/**
* 递归子问题,返回在[1, n]子链表删除元素后的新头节点
*/
ListNode tem = removeElements(head.next, val, depth + 1);
System.out.print(depthScale);
System.out.println("After remove " + val + ":" + tem);
ListNode res;
/**
* 如果头节点就是要删除的节点,那就要返回第二个节点
* 如果不是,那head一定要和tem链接上
*/
if (head.val == val){
res = tem;
}
else{
head.next = tem;
res = head;
}
System.out.print(depthScale);
System.out.println("Return:" + res);
return res;
}
/**
* 定义一个打印横线的方法,递归的层次越深,横线越多
*/
public String depth(int depth){
StringBuilder str = new StringBuilder();
for (int i = 0; i < depth; i++) {
str.append("--");
}
return str.toString();
}
}
class ListNode {
public int val;
public ListNode next;
public ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
public ListNode(int val) {
this.val = val;
}
public ListNode(){}
/**
* 将一个数组转换为链表
* 返回值是链表的头节点
*/
public ListNode(int[] arr){
if (arr == null || arr.length == 0){
throw new IllegalArgumentException("数组是空的");
}
this.val = arr[0];
ListNode prev = this;
for (int i = 1; i < arr.length; i++) {
prev.next = new ListNode(arr[i]);
prev = prev.next;
}
}
@Override
public String toString(){
StringBuilder str = new StringBuilder();
ListNode curr = this;
while (curr != null){
str.append(curr.val + "——>");
curr = curr.next;
}
str.append("null");
return str.toString();
}
}
注意:removeElements()方法的返回值类型如果改成void,是不能创建链表的,因为递归函数的结果需要和前面的链表连接起来
递归算法的复杂度分析
不是有递归的函数复杂度就一定是O(nlogn)
只进行一次递归
假设递归深度为depth,只进行一次递归时,depth一般情况下都是logn,再加上其他的操作T,总的时间复杂度为O(T * logn)
/**
* 计算x的n次幂,x大于等于0
* 时间复杂度为O(logn)
*/
public class Algorithm {
public static void main(String[] args) {
System.out.println(pow(2, 3));
}
public static double pow(double x, int n){
if (n == 0){
return 1.0;
}
/**
* 先计算x的n / 2次幂,然后求平方
* 注意n / 2向下取整可能会损失一位,所以要判断一下
*/
double t = pow(x, n / 2);
if (n % 2 != 0){
return x * t * t;
}
return t * t;
}
}
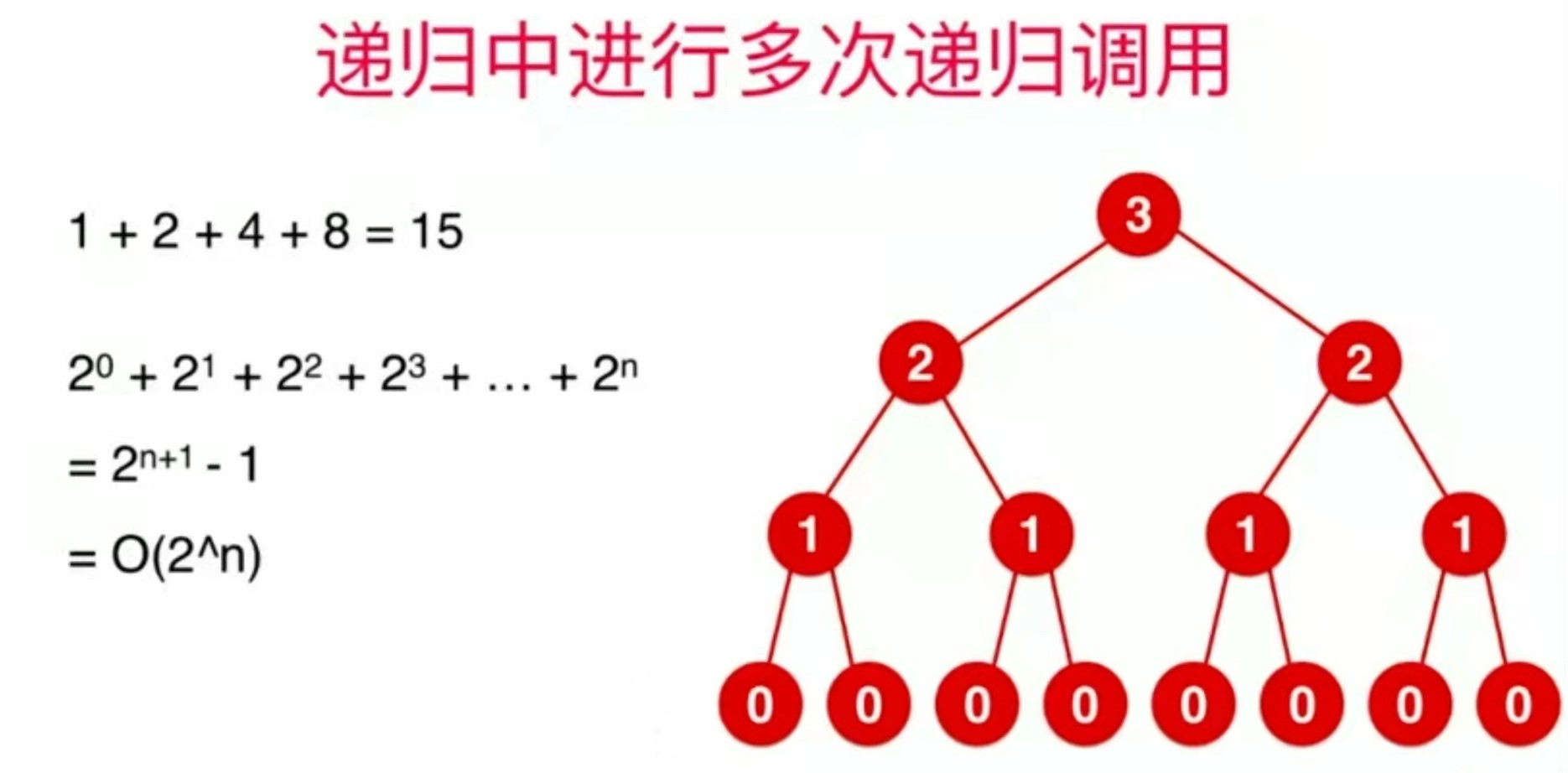
多次调用递归
递归运行主要的时间消耗是递归调用的次数而不是深度,上述只调用一次递归的情况中,调用的次数等于递归深度,而当多次调用递归时,要关注其真正调用了多少次
在这种情况中,虽然递归深度只有4,但是每次进行递归调用的次数都翻倍,其时间复杂度为O(2^n)
而归并排序法每层进行的操作都是n,递归深度为logn,时间复杂度为O(nlogn)






 浙公网安备 33010602011771号
浙公网安备 33010602011771号