[Problem15]欧拉

自己没想出。google的结果是：用数学上的组合方面的知识可轻松搞定。

这里，关键是通过这一题复习排列组合相关的数学知识（也许你的项目中很少用到数学知识来解决编程问题，但是数学还是非常有益的）：
1. 排列组合的公式

 

 

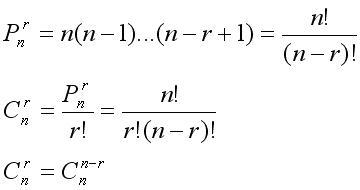
2. 排列组合的最本质两个法则：乘法法则——分步，和加法法则——分类。

(1)加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N＝m1＋m2＋m3＋…＋mn种不同方法． 　　(2)乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有N＝m1×m2×m3×…×mn种不同的方法． 　　这里要注意区分两个原理，要做一件事，完成它若是有n类办法，是分类问题，第一类中的方法都是独立的，因此用加法原理；做一件事，需要分n个步骤，步与步之间是连续的，只有将分成的若干个互相联系的步骤，依次相继完成，这件事才算完成，因此用乘法原理． 

 

关于本题： 

1. 本质上就是一个从m+n步里选出m步往一个方向的组合问题。

小虫路线计数(I)：现在有个虫子在(0,0)，每步只能往x,y的正方向走，要求走到(m,n)，问有多少种路径（有一步不同的路径就视作不同的路径）。

这 玩意高中肯定都做过，因为每步只能走正方向，所以小虫不管怎么走，一共都是走m+n步到(m,n)，而这m+n步里，必然是m步向右，n步向上，所以说只 要从m+n步里选出其中的某m步，规定其向右走就行了。当然，你从中选出n步，规定其向上，得到的答案也是一样的。答数是 C(m+n,m)=C(m+n,n)。

在百度百科复习：排列组合和数学归纳法

2. 算法就是计算40! / (20!) * (20!)。写个f(n)来计算n!。仍然有值得注意的事项：

1） n!的值超出了unsigned long long的范围。对于c#和Jave来说，他们有bigInteger；但是对于c++，数据类型的选择就需要考虑清楚了。这里，计算n!，只能用double了。double能表示的数字的最大值远远远远大于unsigned long long，虽然大家都是占8bytes。double的内存表示是科学计数法，其取值范围是-1.7*10(-308)～1.7*10(308)；unsigned long long是0~1844674407370955161(10(18)左右)。

2）因为是用double数据类型来表示需要的整数的乘积，因此在计算乘积过程中，必然会出现一定的误差，不像整数相乘那么精准。见下面代码中的comment。

#include <iostream>
using namespace std;

// n! 从n到1乘到乘积上，算出的结果是正确的整数带了0.000006 (137846528820.00006)，应该是double数值的精度表示导致的（比如1999999 = 1.999998*e6）。
double f(int n)
{
    double result = 1;
    int i=n;
    while(i>=1)
    {
        result *= i;
        i--;
    }
    return result;
}

// n! 从1到n乘到乘积上，算出的结果是正确的整数(137846528820)。
double JieChen(int n)
{
    if(n == 1)
    return 1;
    else
    return n * JieChen(n - 1);
}

int _tmain(int argc, _TCHAR* argv[])
{
    double result1 = JieChen(20);    
    double result2 = JieChen(40);
    result2 /= result1;
    result2 /= result1;
    cout << result2 << endl;
    return 0;
}