吴恩达机器学习笔记——拟合（一）

监督学习

1. 说明：
     监督学习分为是指有一批确定标签的数据下训练神经网络，然后来对新数据进行预测。常见要解决的问题有两类，一是回归问题，二是分类问题。
     无监督学习主要处理聚类问题，暂不讲。

回归问题

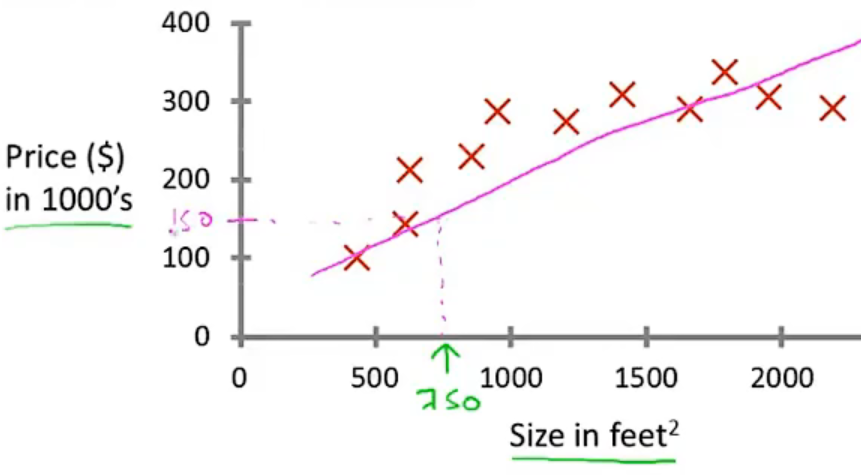
1. 比如根据房子的面积估计房价。我得有一批直到房子面积和对应价格的数据，然后拟合曲线，然后根据曲线来预测新值。
   

分类问题

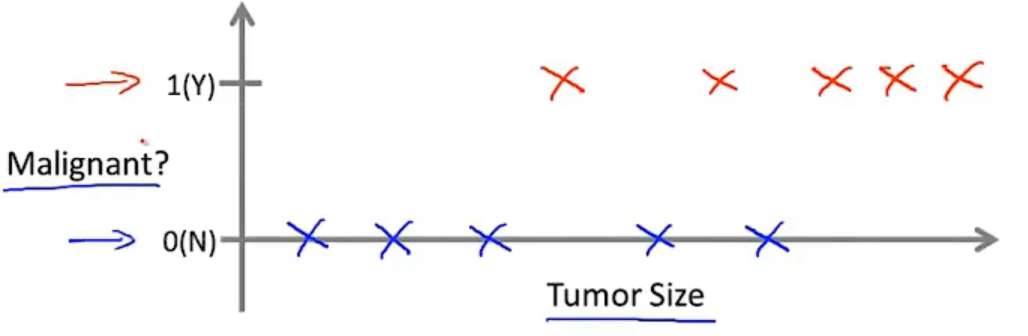
1. 分类问题可以是简单的是或者不是，即0/1问题（一个特征）
   
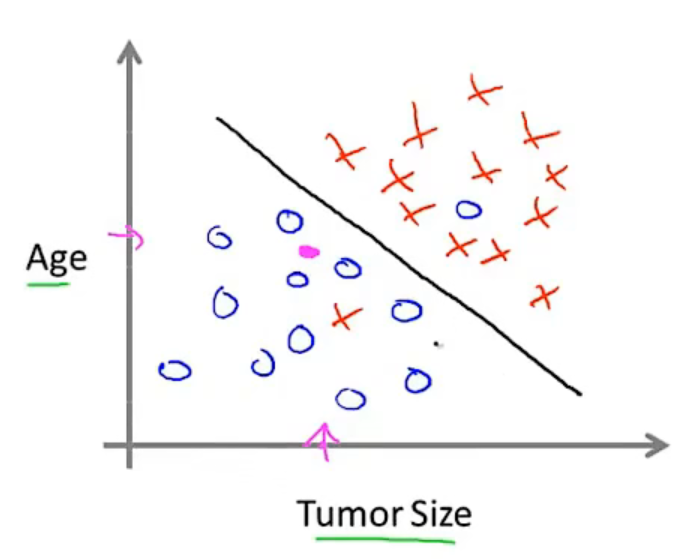
2. 也可以是两个特征，就需要一个线来划分。如果是三个特征就是平面来划分
   

代价函数（损失函数）

1. 说明
     下面的例子是针对回归问题的，还是以面积和房价模型来进行说明。
   
     所谓代价函数即是衡量假设函数拟合度的函数，值越小，拟合度越高。

假设函数（预测函数）

1. 说明：
     要让这条曲线最符合所有已知数据也即是对房价拟合用的假设的一个函数：这里是一个一元一次函数
   \[h_{\theta} \left ( x \right )= \theta _{1}x+\theta _{0} \]

最小二乘法（均方差）代价函数

1. 说明：
     要让这条曲线最贴合所有已知数据，那一个很基本的方法是最小二乘法，也即是下面求函数的最小值。\(m\)表示数据个数，\(i\)表示第几个，\(y^{i}\)表示某个已知数据的\(y\)值（房价），\(h_{\theta} \left ( x^{i} \right )\)表示拟合函数的在该处预测值，\(\frac{1}{m}\)表示平均值。

   \[J\left(\theta _{0},\theta _{1} \right ) = \frac{1}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )^{2} \]

     将\(h_{\theta} \left ( x \right )= \theta _{1}x\)函数带入：这里我们先假设函数过原点，没有参数\(\theta _{0}\)

   \[J\left(\theta _{1} \right ) = \frac{1}{m}\sum_{i=1}^{m} \left ( \theta _{1}x-y^{i} \right )^{2} \]

     将函数完全平方展开，把求和符号移进去，我们可以得到一个关于\(\theta _{1}\)的一元二次方程，所以其代价函数是一个二维平面上的曲线。(下图的\(w\)就是\(\theta _{1}\))
   

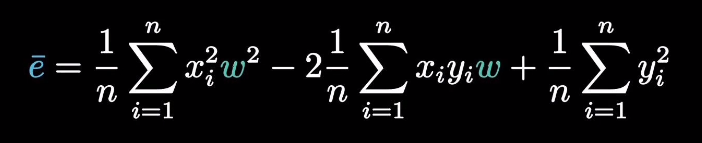
2. 将不同斜率值的\(\theta _{1}\)带入函数，我们可以得到一个关于 \(\theta _{1}\)和\(J\left(\theta_{1} \right )\)的凸函数代价函数，存在一个\(\theta _{1}\)的值使得\(J\left(\theta_{1} \right )\)可以取到最小值。
   

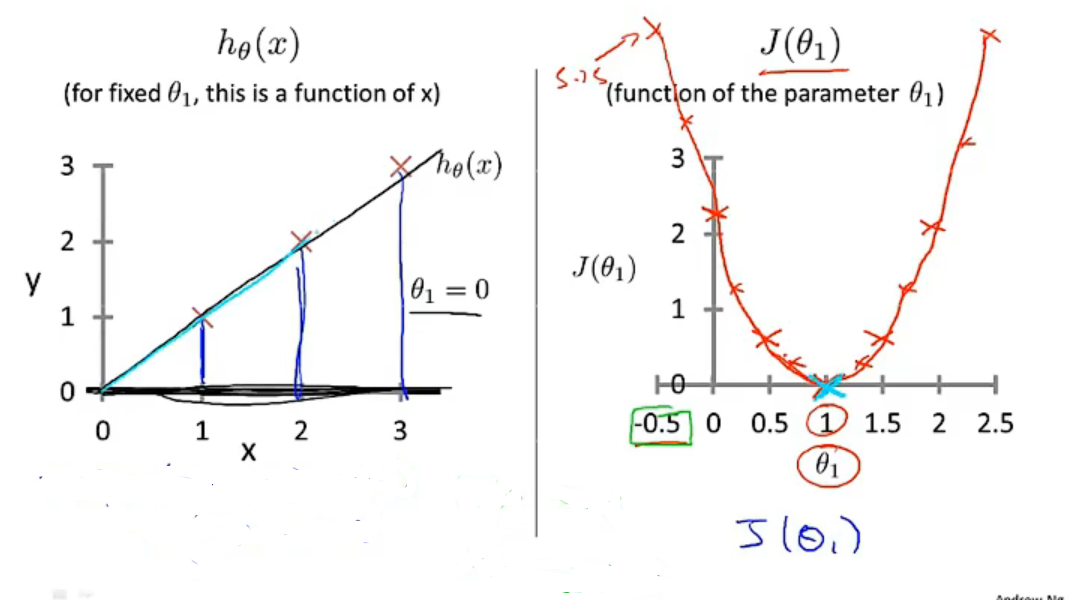
3. 函数如果不过原点，还存在一个截距\(\theta _{0}\)， 此时的代价函数是一个曲面：
   
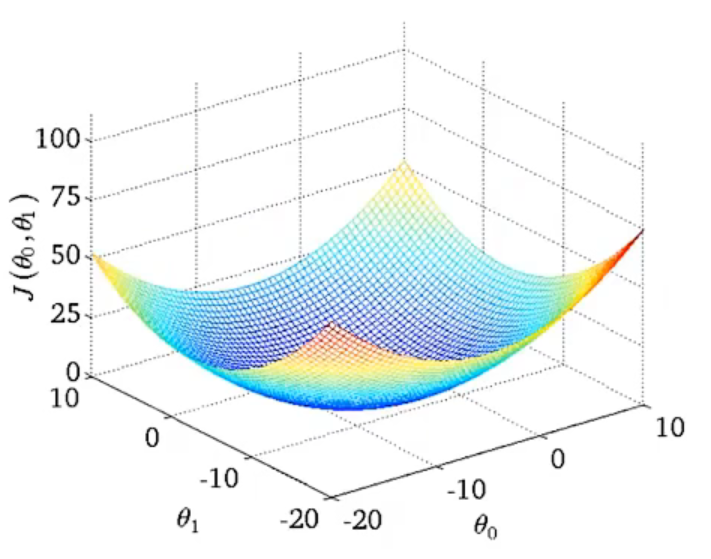
     从上往下看，我们可以用等高线来表示相同\(J\left(\theta _{0},\theta _{1} \right )\)值的\(\theta _{0}\)和\(\theta _{1}\)点集：
   
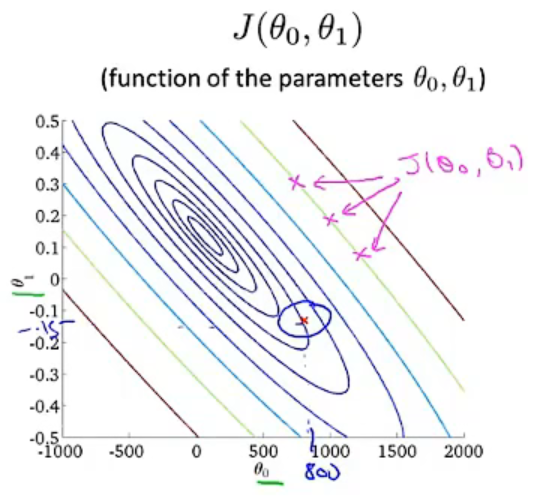
     当我们的点越接近圆心，也就是\(J\left(\theta _{0},\theta _{1} \right )\)值越小时，带有\(\theta _{0}\)和\(\theta _{1}\)两个参数的假设函数\(h_{\theta} \left ( x^{i} \right )\)，其拟合度越好。
   

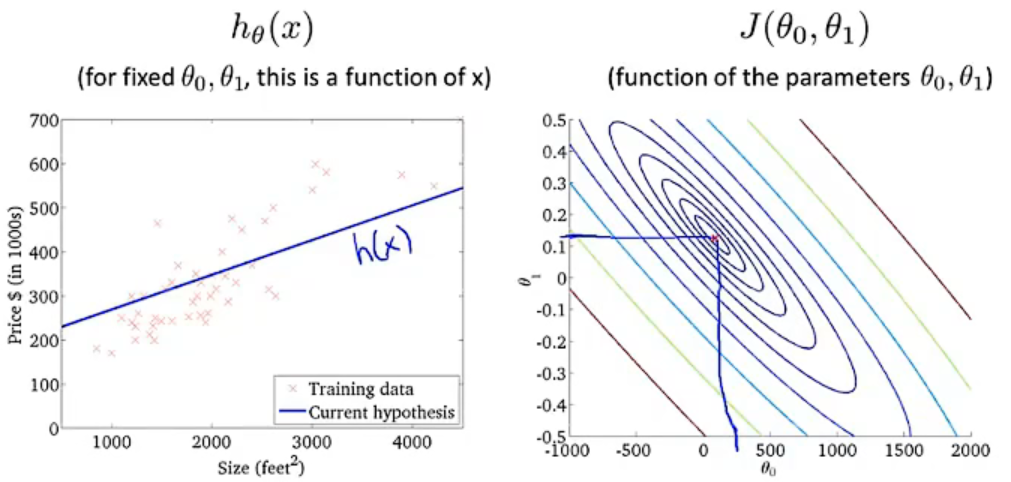
4. 补充：
     实际上一个假设函数，还可以不止两个维度，多个维度也是可以的。

梯度下降

1. 说明：
     代价函数我们找到了，但实际上上面讲的凸函数，我们实际上是不知道他的最小值在哪里的，而梯度下降算法就是为了帮助我们找到这个最小值。

梯度算法的定义：预测函数只有一个参数\(\theta _{1}\)时，参数的更新

1. 说明：
     这个时候我们知道代价函数是一个凸函数，我们理想的一种逻辑是，在某个点上开始后（初始化），每一次迭代，点都朝着最低点靠近一些，也就是说，函数需要知道自己到底在最低点的哪一边，这个时候，一个很自然的判断是凸函数的斜率，斜率在最低点的两边是相反的。
   
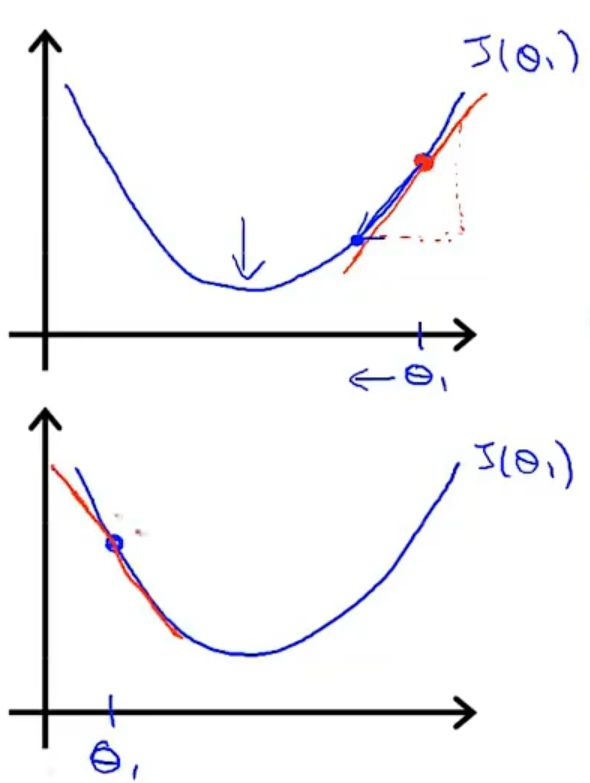
     于是，每次迭代更新\(\theta _{1}\)的公式我们就可以定义成：\(:=\)是定义符号，不是等于，这里和代码里面的赋值一个意思，也就是新的\(\theta _{1}\)等于旧的\(\theta _{1}\)减去后面那一坨。\(\alpha\)表示学习率，也就是每次迭代移动倍率。\(\frac{\partial }{\partial \theta _{1}}J\left ( \theta _{1} \right )\)表示斜率，是一个求导公式。
   \[\theta _{1}:= \theta _{1}-\alpha \frac{\partial }{\partial \theta _{1}}J\left ( \theta _{1} \right ) \]
     上面这个公式的意思就是，每次迭代，新的\(\theta _{1}\)等于旧的\(\theta _{1}\)减去对饮斜率乘以一个移动倍率，在最低点右边斜率是一个正数，新的\(\theta _{1}\)变小，点往左移，且斜率越大，移动越快。
     \(\alpha\)如果过小，会导致移动过慢，而值过大，则有可能点在最低点两边反复横跳。

梯度算法推导：预测函数只有两个参数\(\theta _{0}\)和\(\theta _{1}\)时，参数的更新

1. 说明：
     上面已经给我们说明基本的梯度下降算法对单个参数的处理，这里我们把第二个参数也带入进来。此外，上面的式子没有把导数值解开，这里我们将解导数。

   \[\theta _{0}:= \theta _{0}-\alpha \frac{\partial }{\partial \theta _{0}}J\left ( \theta _{0},\theta _{1} \right ) \]
   \[\theta _{1}:= \theta _{1}-\alpha \frac{\partial }{\partial \theta _{1}}J\left ( \theta _{0},\theta _{1} \right ) \]

2. 解导数：上面式子主要是\(\frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right )\)需要求解
     我们知道损失函数:

   \[J\left(\theta _{0},\theta _{1} \right ) = \frac{1}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )^{2} \]

     所以：

   \[\frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right )=\frac{\partial }{\partial \theta _{j}} \left ( \frac{1}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )^{2}\right ) \]

     因为被导函数是一个连加的函数，根据导数的加法定律(分别求导再相加)，可以写成：

   \[\frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{m}\sum_{i=1}^{m} \frac{\partial }{\partial \theta _{j}} \left ( \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )^{2}\right ) \]

     此时的被导函数是一个复合函数（\(h_{\theta} \left ( x^{i} \right )-y^{i}\)和一个指数复合），根据复合函数求导法则（先对指数求导，再对\(h_{\theta} \left ( x^{i} \right )-y^{i}\)求导），可得：

   \[\frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{m}\sum_{i=1}^{m} 2\left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right ) \frac{\partial }{\partial \theta _{j}} \left ( \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )^{2}\right ) \]

     而预测函数是

   \[h_{\theta} \left ( x \right )= \theta _{1}x+\theta _{0} \]

     所以：只需要替换需要求导部分的

   \[\frac{\partial }{\partial \theta _{j}}J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{m}\sum_{i=1}^{m} 2\left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right ) \frac{\partial }{\partial \theta _{j}} \left ( \theta _{1}x+\theta _{0} -y^{i} \right ) \]

     于是，对\(\theta _{0}\)和\(\theta _{1}\)求导就有：对\(\theta _{0}\)求导，其他参数皆视作常数；对\(\theta _{1}\)求导，其他参数皆视作常数

   \[\frac{\partial }{\partial \theta _{0}}J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{m}\sum_{i=1}^{m} 2\left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )\times 1 \]
   \[\frac{\partial }{\partial \theta _{1}}J\left ( \theta _{0},\theta _{1} \right )=\frac{1}{m}\sum_{i=1}^{m} 2\left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )\times x^{i} \]

     整理一下：

   \[\frac{\partial }{\partial \theta _{0}}J\left ( \theta _{0},\theta _{1} \right )=\frac{2}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right ) \]
   \[\frac{\partial }{\partial \theta _{1}}J\left ( \theta _{0},\theta _{1} \right )=\frac{2}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )x^{i} \]

     至于吴恩达计算里面为什么一开始有个\(\frac{1}{2}\)，主要是为了消掉求导产生的2，实际不影响结果。
     最后将求导结果放回梯度算法：

   \[\theta _{0}:= \theta _{0}-\alpha \frac{2}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right ) \]
   \[\theta _{1}:= \theta _{1}-\alpha \frac{2}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )x^{i} \]

3. 补充：
     上面说的梯度下降算法由于每次下降都要求所有点计算之和，所以计算量比较大，这种算法叫做“批量梯度下降法”

梯度算法推广：多特征(参数)梯度算法

1. 说明：
     回到房子面积和价格的关系例子，上面的算法只涉及一个权重\(\theta_{1}\)（也就是最开始房子面积的权重）和一个截距\(\theta_{0}\)，但现实还有很多因素要考虑，比如在几环、房子的房间数、距离地铁的距离等等，把这些因素考虑进去，那我们要拟合的就不再是一条线，而是更高纬度的数据。
     其预测函数可以写成：吴恩达加了个\(x_{0}\)，且\(x_{0}=1\)，我直接省了，因为我这里不写成矩阵形式
   \[h_{\theta} \left ( x \right )=\theta _{0}+\theta _{1}x_{1}+\cdots +\theta _{n}x_{n} \]
     损失函数则是：
   \[J\left ( \theta _{0},\cdots \theta _{n} \right )=\frac{1}{m}\sum_{i=1}^{m}\left ( h_{\theta} \left ( x^{i} \right )-y^{i}\right )^{2} \]
     写成下面这个好看点：
   \[J\left ( \theta \right )=\frac{1}{m}\sum_{i=1}^{m}\left ( h_{\theta} \left ( x^{i} \right )-y^{i}\right )^{2} \]
     同样，梯度算法则是：
   \[\theta _{j}:= \theta _{j}-\alpha \frac{\partial }{\partial \theta _{j}}J\left ( \theta\right ) \]
     解开导数：截距那个\(x^{i}_{j}=1\)
   \[\theta _{j}:= \theta _{j}-\alpha \frac{2}{m}\sum_{i=1}^{m} \left ( h_{\theta} \left ( x^{i} \right )-y^{i} \right )x^{i}_{j} \]

特征缩放(数据归一化)

1. 不同特征(\(x_{j}\))由于取值范围不一样，比如房子面积和房间数，会导致其\(\theta_{j}\)取值范围也有较大差异，进行梯度下降的时候会延长迭代周期，所以要新进归一化，把不同的特征的数值（训练数据）都局限在差不多的取值范围内：
   
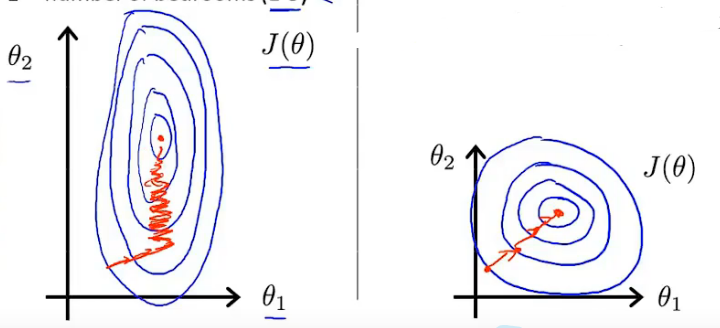
2. 归一化：所有参训数据都要进行下面的计算
   \[x_{j}:=\frac{x_{j}-avg\left ( x_{j} \right )}{max\left ( x_{j} \right )} \]
     什么意思呢？我们可以把最大值看成一个总长度，那么某个具体的\(x_{j}\)除以最大的\(x_{j}\)相当于其占总长度的比值，在\(\left [ 0,1 \right ]\)内，但是这个具体的\(x_{j}\)减去平均值再除以最大值，相当于把刚才的占比往后推了0.5，所以这个比值变成了在\(\left [ -0.5,0.5 \right ]\)，一般来说取值范围要有正有负才好，所以要往这么做。

非线性函数拟合（特征和多项式回归）

1. 说明：
     上面说的拟合回归问题，我们的拟合曲线都用的是多（一）元一次的预测函数，但有时候一条直线是不能很好的拟合我们的数据，这个时候我们就需要进行非线性的拟合了：
   
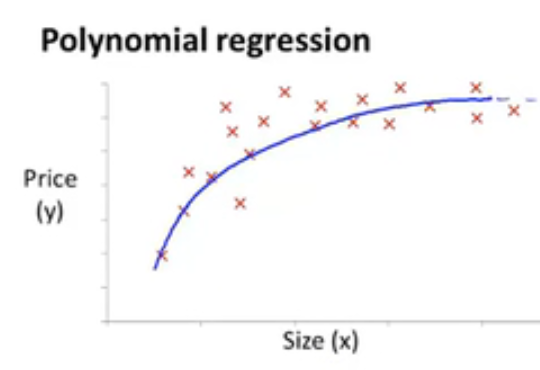
     这种形状的数据我们可以根据大致走向确定用什么函数作为预测函数，上图的结构和幂函数比较像，那我们就可以用幂函数作为预测函数：下面是式子只是个例子，可以是其他幂函数
   \[h_{\theta }\left ( x \right )=\theta _{0}+\theta _{1}x+\theta _{2}\sqrt{x} \]

2. 注意：
     要注意的是归一化的不是单个数据，而是\(\theta _{j}\)后面的整个特征参数，比如上面的\(\sqrt{x}\)整个进行归一化，而不是单独的\(x\)。
3. 备注：
   • 这里会觉得特征参数好难选，可以搞很多，又有很多形式，指数、幂等等，后面会将如何处理。

矢量

1. 说明：
   其实就是假设函数（预测函数）和梯度可以写成矩阵形式，这个在我随笔《卷积神经网络》的感知机那部分有写，可参考。