道长的算法笔记:动态规划经典模型
(一)背包模型
背包问题的各种变形可以搜一下背包九讲,事实上我们只需要掌握三种零一背包、多重背包、完全背包三种基础问题即可,其它复杂的问题往往都可以转为这三种基础的背包问题。更多细节可参考这篇笔记,下面给出提纲。
- 零一背包 & 完全背包
- 为什么二者的状态转移方程如此相似?
- 零一背包逆序遍历优化
- 完全背包状态重叠优化
- 为什么二者的状态转移方程如此相似?
- 多重背包 & 混合背包
- 由于无限拾取的物件,数量不超过体背包容量除以其体积,因而混合背包能被转为多重背包
- 多重背包如何优化
- 按类分组的二进制拆分优化
- 按余分组的单调队列优化
- 基于费用的背包变种问题
- 要求拾取费用小于等于容量,背包价值优化问题
- 要求拾取费用恰好等于容量,背包方案数量问题
- 要求拾取费用大于等于容量,背包价值优化问题
- 背包最优路径数量问题(类似问题也在最短路模型中出现,例如要求计算最短路条数)
- 利用互斥关系把具有树形关系的背包转为分组背包
- 大容积背包问题
(1.1) 背包问题蕴含的组合数学
其基础母题,网上已有很多详细的教学,本篇主要解决讨论背包方案数的几个难点,例如LeetCode上面的 LC0377、LC1155,大容积背包问题如何解决,以及零一背包的奇怪变种问题,例如洛谷 P1156 等等。下面先从两道LeetCode问题讲起,
// LC0377
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<int> dp(target + nums.size(), 0);
dp[0] = 1;
for(int j = 0; j <= target; j++){
for(int i = 0; i < nums.size(); i++){
if(j >= nums[i]){
dp[j] += dp[j - nums[i]];
}
}
}
return dp[target];
}
};
本题主要的难点在于,元素之间不同的排列也被认为是不同的方案。其实只要更换一下循环的内外层关系即可。也就是说,先循环物品,再循环背包容积,更新出来的方案数是组合,如果先循环背包容积,再循环物品,更新出来的方案是排列。
一般背包问题中,我们循环均以枚举物品,再枚举背包容积的方式更新。如果是分组背包问题则会先枚举一个组,再枚举容积,再枚举组内问题,这个过程相当于把一个组当做一个物品,只不过这个物品存在多种不同的取值,我们仅能从中取一种值,下面一道 LC1155 便是这么一个思想。下面我们图解 LC0377 这道题,这道题是一个多重背包的变种。
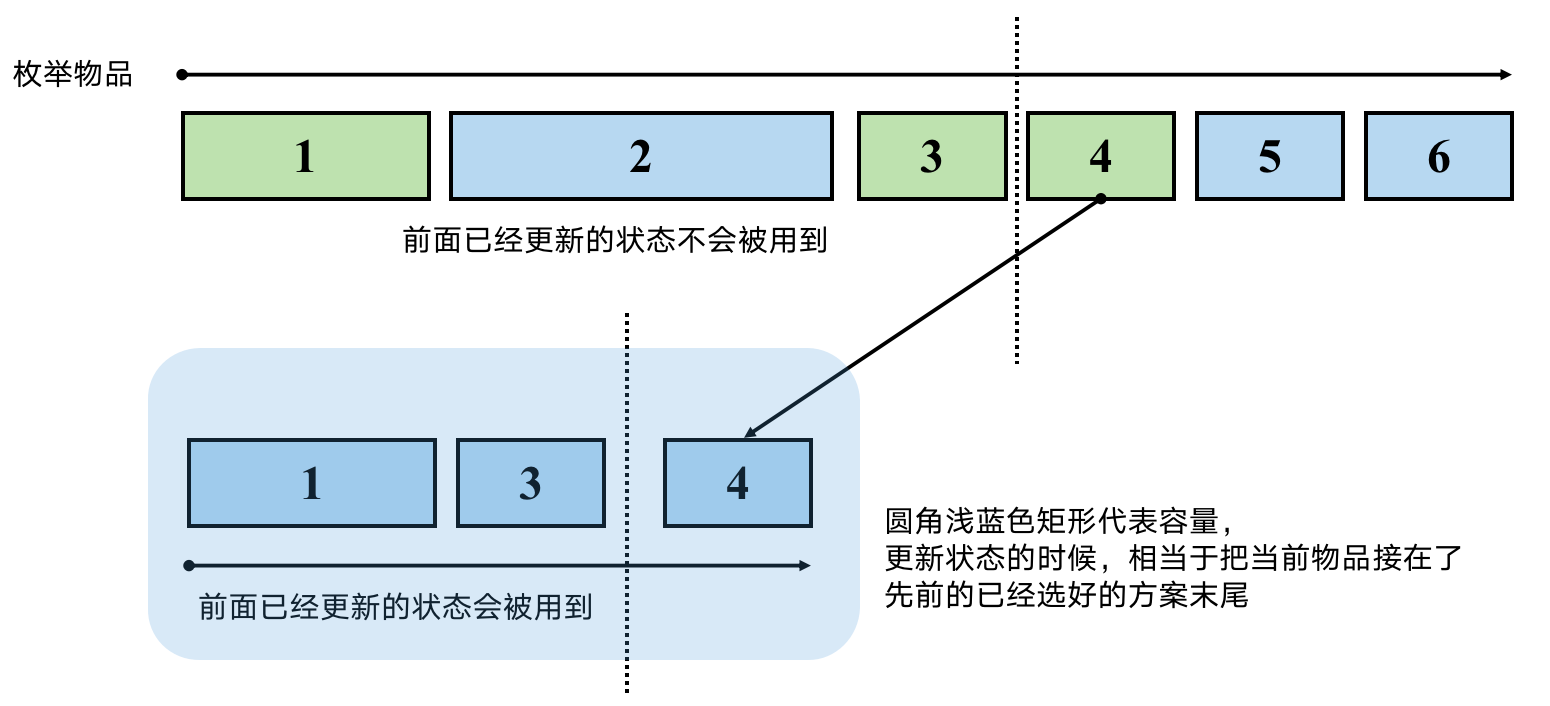
此时循环的含义是使用当前物品去更新不同的体积状态,物品是从前往后遍历,且只被使用一次的用于更新体积,更新体积的时候,我们使用的也是前面已被更新的状态。然而,外层枚举体积,内层枚举物品的时候,当前体积的状态可能会被多个物品更新一遍,且更新使用的也是前面已经被更新的状态,我们感性层面,会发现后者考虑的方案数明显变多了。
我们每个物品取得的容积抽象为长度,为了作图方便,不妨假设价值和容积数值是一样,那么先枚举背包容积再枚举物品,则如下图所示,通过对比会发现,先枚举物品再枚举体积,只考虑了其中某种顺序的方案,其含义相当于组合,而若先枚举背包容积再枚举物品则会考虑不同顺序的状态。
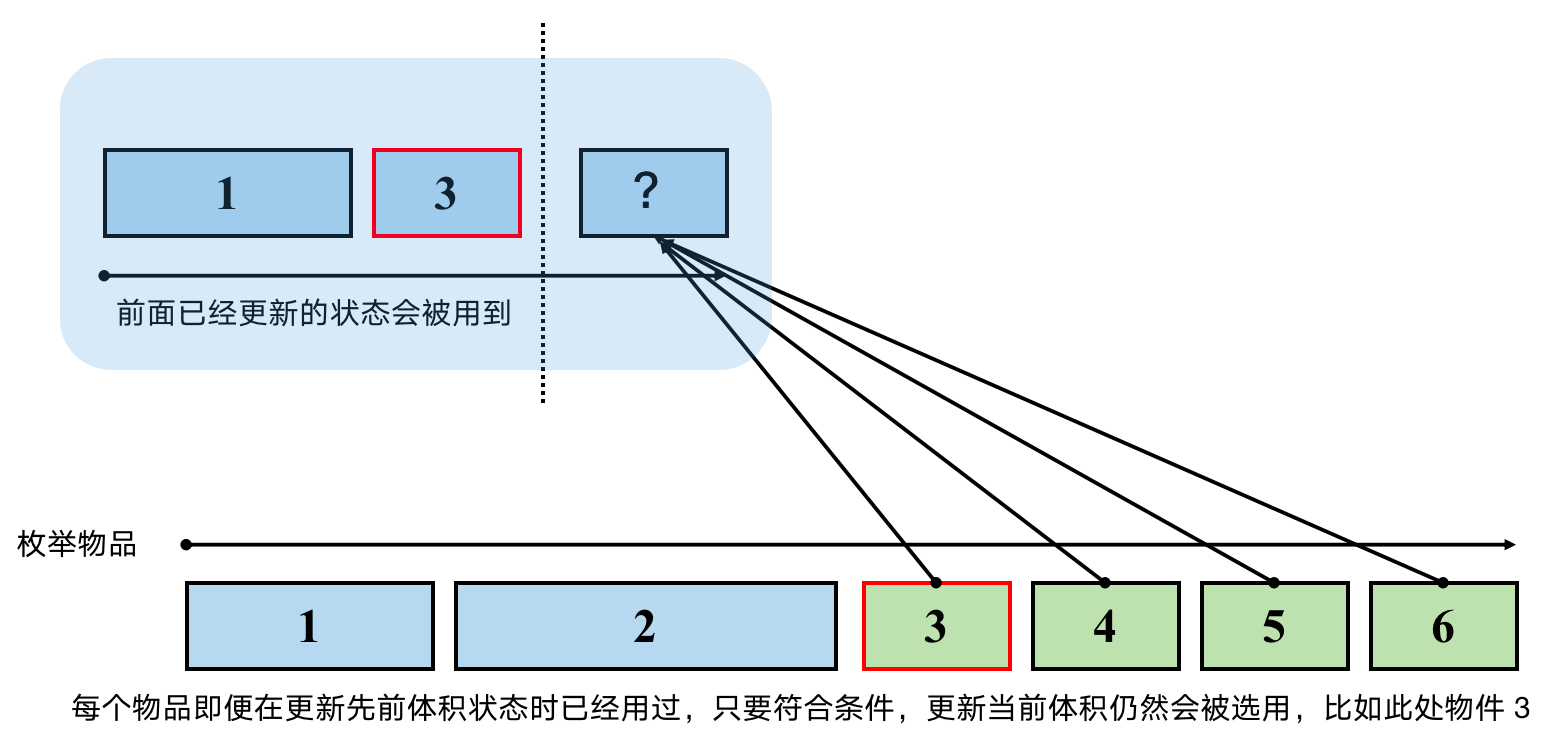
在做背包问题的时候,朴素的状态转移通常会定义两个维度 \(\text{dp[i][j]}\),代表第 \(i\) 个物品时刻,背包容积 \(j\) 能够取得的最大价值,我们更新状态之前经常会无脑来一句,\(\text{dp[i][j] = dp[i - 1][j]}\),对于大多问题来说,这种做法是正确,但在一些问题中添加这句赋值语句反而会出错。
这种困惑是因为没有理解 \(dp\) 数组状态所定义的含义,如果当状态允许从先前的状态中转移而来,那么这句赋值要添加,如果当前状态不允许从先前的状态中转移而来,那么这句赋值语句不可以添加。比如投掷骰子这道题,是恰好等于给定骰子能够投出点数合计等于 \(\text{target}\) 所有方案数,而不是小于等于给定骰子能够投出点数合计等于 \(\text{target}\) 所有方案数,所以不应该添加这句赋值。
// LC1155
int numRollsToTarget(int n, int k, int target) {
int MOD = 1e9 + 7;
vector<vector<int>> dp(n + 1, vector<int>(target + 1, 0));
dp[0][0] = 1;
for(int i = 1; i <= n; i++){
for(int j = 0; j <= target; j++){
// dp[i][j] = dp[i - 1][j]; // 这一步极其关键, 本次的状态不可以从上一次状态转移而来,所以不允许添这句赋值!
for(int u = 1; u <= k; u++){
if(j - u >= 0){
dp[i][j] = (0LL + dp[i][j] + dp[i - 1][j - u]) % MOD;
}
}
}
}
return dp[n][target] % MOD;
}
// 优化空间之后,每次更新 j 之前需要清零 dp[j] 以免计入上一次状态计算的结果
int numRollsToTarget(int n, int k, int target) {
int MOD = 1e9 + 7;
vector<int> dp(target + 1, 0);
dp[0] = 1;
for(int i = 1; i <= n; i++){
for(int j = target; j >= 0; j--){
dp[j] = 0;
for(int u = 1; u <= k; u++){
if(j - u >= 0){
dp[j] = (0LL + dp[j] + dp[j - u]) % MOD;
}
}
}
}
return dp[target] % MOD;
}
(1.2) 背包问题大容积处理
如果背包容积非常巨大,远超我们能够接受的空间复杂度范围,此时一种转化思路便是把所有物品的价值加总在一起,枚举不同价值状态之下所需要的最小体积,然后搜索体积小于等于给定约束时候的最优方案。
void big_vol_knap(int v[MAXN], int w[MAXN], int dp[MAXN]){
int wsum = 0;
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%d %d", &v[i], &w[i]);
wsum += w[i];
}
memset(dp, 0x3f, sizeof(dp));
dp[0] = 0;
for(int i = 1; i <= n; i++){
for(int j = wsum; j >= w[i]; j--){
dp[j] = min(dp[j], dp[j - w[i]] + v[i]);
}
}
int ans = 0;
for(int i = 0; i <= wsum; i++){
if(dp[i] <= m){
ans = max(ans, i);
}
}
printf("%d\n", ans);
}
(1.3) 背包问题场景应用
假设你在玩一个游戏,你的游戏角色有两种属性值 \(E\) 和 \(H\),游戏中会出现共\(n\)个道具,第 \(i\) 个道具会在 \(t_i\) 时刻出现,道具出现之后仅能使用一次,使用道具是在一瞬间完成的,不耗时间,对于每个道具可以选择增加 \(e_i\) 属性值 \(E\),或者增加 \(h_i\) 属性值 \(H\)。如果 \(H\) 达到阈值 \(h\) 则会通关。不妨把属性 \(H\) 称为闯关值,属性 \(E\) 称为生命值。游戏开始时刻,生命值\(E=s\),生命值会每过一个单位时间,会减少\(1\),闯关值 \(H=0\),我们需要计算通过游戏需要多少时间,如果无法通过,则要算出最多需要多长时间。
本题状态量极多,并且 \(1 \leq n \leq 5000,1 \leq h\leq 10^4\),\(s,t_i,e_i,h_i\) 最大可达 \(10^8\) 数据范围较大。本题来自于清华大学暑期训练营,其实这题是对洛谷 P1156 这题的加强版,之所以说是加强版是因为本题数据范围更大,并且会物品可能会在相同时刻出现。初看之下,本题状态多得会让人有一点无所适从,但是生命值、出现时刻这些变量实际是能够整合在一起的,我们知道生命值是按单位时间减少的,物品也是在某个单位时刻出现的,我们只需要考虑当前生命值能不能坚持到某个物品出现就好。
如果能通过则输出最少用时,如果无法通过则输出最长存活时间,给人感觉似乎需要维护两个 \(dp\) 数组,一个最大兼一个最小。实则不然,采用贪心的做法便能解决最短的通过时间。我们按照物品出现时刻从小到大,闯关值、苟命值从大到小排序。因为我们的核心目标是通关,其次无法通过的时候才考虑能苟命多久,因而如果物品在相同时刻出现,我们优先考虑能帮助我们提高更多闯关值的,如果二者闯关值也一样,再考虑谁更能帮我们苟命。排序之后,对物品做扫描,如果我们当前闯关值状态已经达到 \(j\),当前状态能够苟到某物品 \(i\) 出现,并且这个物品提供的闯关值满足 \(j + h_i > h\),那么这个物品出现的时刻也即最短通过时间。
分析至此,会发现我们能否通过,取决于能在苟到某个能帮我们冲破阈值的物品出现,因而我们需要维护的信息便是,闯关值 \(j\) 状态之下能苟多久。也就是说,我们需要最大化苟命的时间。我们先按贪心思想排序,再对已排序的数组进行动态规划,下面给出基于洛谷 [P1156] 修改得到的 AC 代码。
#include <bits/stdc++.h>
#include <limits>
using namespace std;
typedef long long llong;
typedef unsigned long long ull;
typedef pair<int, int> ii;
typedef tuple<int, int, int> iii;
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
#define MAXN 500005
typedef struct _Trash{
int t, f, h;
bool operator<(const struct _Trash& other) const{
if (t != other.t) {
return t < other.t;
}else if(h != other.h){
return h > other.h;
}else{
return f > other.f;
}
}
} Trash;
llong dp[MAXN];
Trash ts[MAXN];
void debug_print_input(int n){
for (int i = 1; i <= n; i++){
printf("%d %d %d\n", ts[i].t, ts[i].f, ts[i].h);
}
printf("\n");
}
int main(){
int d, g, t, f, h, s;
scanf("%d %d", &d, &g);
scanf("%d", &s);
for (int i = 1; i <= g; i++) {
scanf("%d %d %d", &t, &f, &h);
ts[i] = {t, f, h};
}
sort(ts + 1, ts + 1 + g);
// debug_print_input(g);
memset(dp, 0xcf, sizeof(dp));
dp[0] = s;
for (int i = 1; i <= g; i++) {
for (int j = d; j >= 0; j--){
if(dp[j] < ts[i].t)
continue;
if(j + ts[i].h >= d){
printf("%d\n", ts[i].t);
return 0;
}
dp[j + ts[i].h] = max(dp[j + ts[i].h], dp[j]);
dp[j] += ts[i].f;
}
}
printf("-1\n");
printf("%lld\n", dp[0]);
return 0;
}
回顾上面的代码会发现,本题实际是一个零一背包的变型问题,背包的容量就是需要达到的阈值,如果大于等于这个阈值,我们也就通关了。常见的零一背包是拾取物品或舍弃物品,但在本题的应用中变成了,使用物品闯关或者苟命。\(\text{dp[j]}\) 代表闯关值达到 \(j\) 时刻当前生命值能够持续多久。显然,初始状态 \(dp[0] = s\),我们要对两种情况进行特判,首先如果 \(dp[j]\) 小于物品的出现时刻,说明玩家苟不到当前物品到达,跳过当前状态,如果当前闯关值加上物品提供的闯关值高于阈值则通过,接下来是状态转移,由于使用物品是一瞬间完成的,不消耗任何时间,如果选择闯关,\(\text{dp[j + ts[i].h] = max(dp[j + ts[i].h], dp[j])}\),那么闯关值提高,然后再看当前 \(\text{dp[j]}\) 生命值和先前已经更新的 \(\text{dp[j + ts[i].h]}\) 哪一个苟得更久,保留苟命更久的方案。如果选择苟命,\(\text{dp[j] += ts[i].f}\),闯关值不变,生命值增加。
如果遍历所有物品之后,仍然没有找出一个能够帮助我们通过的方案,说明我们无法通过游戏,此时最长的苟命方案就是每个物品都用来续命,也就是说,我们闯关值始终没有长进,简单物品全部用来续命,最大存活时间即为 \(\text{dp[0]}\),也即闯关值为零的时候,能够苟命的最长时间。
(二)数字三角形模型
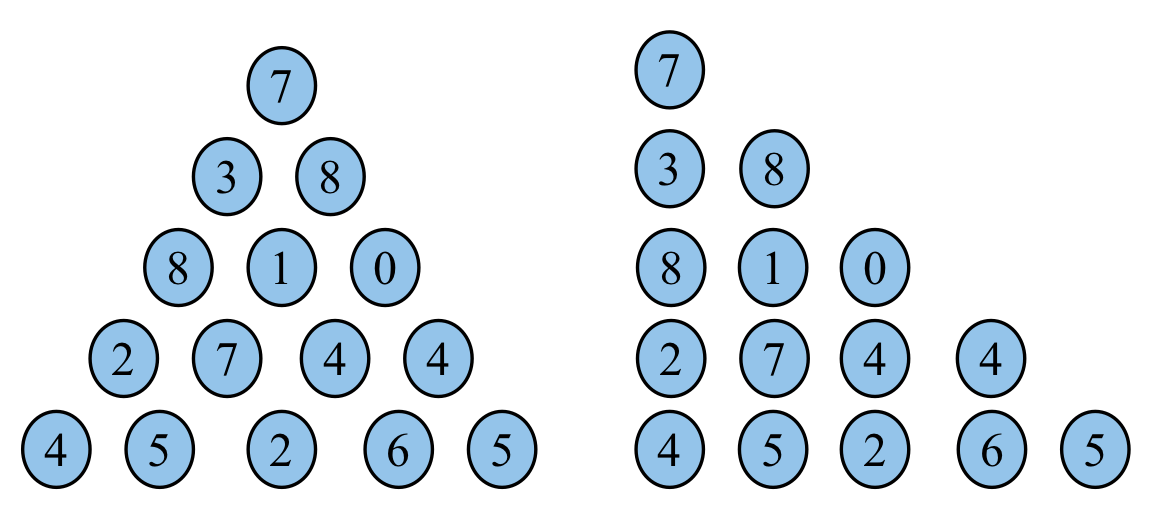
数字三角模型其实也是线性规划问题,但是基于此题的变形很多,我们单独拎出来一个小节进行分析。数字三角的一个简单例子就是杨辉三角。此处给出更一般的版本,给定一个三角形的数堆,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。三角堆看起来并不好处理,所以我们稍微整理一下,使其变成一个下三角形的数堆。
假设所有元素均以存入\(v\),我们不难找出转移方程,本题既可以自顶向下,\(\text{dp[i] = max(dp[i-1][j],dp[i-1][j+1]) + v[i][j]}\) 亦可自底向上\(\text{dp[i] = max(dp[i+1][j],dp[i+1][j+1]) + v[i][j]}\) 求解,参考代码如下所示。
// 自底向上的解法,需要考虑的边界条件更少
void solve_from_bottom2top(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
scanf("%d", &g[i][j]);
}
}
for(int i = 1; i <= n; i++)
dp[n][i] = g[n][i];
for(int i = n - 1; i >= 1; i--){
for(int j = 1; j <= n; j++){
dp[i][j] = g[i][j] + max(dp[i + 1][j], dp[i + 1][j + 1]);
}
}
printf("%d\n", dp[1][1]);
}
// 自顶向下的解法,需要考虑的边界条件更多
void solve_from_top2bottom() {
scanf("%d", &n);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
scanf("%d", &g[i][j]);
}
}
memset(dp, 128, sizeof(dp));// 相当于初始化为一个很小数字
dp[0][0] = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
dp[i][j] = g[i][j] + max(dp[i - 1][j], dp[i - 1][j - 1]);
}
}
int ans = INT_MIN;
for(int i = 1; i <= n; i++){
ans = max(ans, dp[n][i]);
}
printf("%d\n", ans);
}
其实,本题稍作推广能从下三角变为上三角或者矩阵中,通常其变型题目的问法是说,只允许向右或者向下,或者只允许向东或向南,而不可向西或向北走。每个格子代表某种损耗、收益,问你如何最小化损耗或最大化收益。例如 AcWing1015摘花生、AcWing1018最低通行费、AcWing0275传纸条 与 AcWing1027方格取数。尤其需要注意 传纸条、方格取数 两道题的背景略有不同,但其意思都是允许我们在网格中走两次,从左上到右下一共走了两次,试找出两条这样的路径,使得取得的数字之和最大。面对此题第一反应很有可能会用贪心做法,先走一次 dp,再把走过路径置零,再来一次dp,合计两次最大值。
然而,这种做法是不对的,因为第一次 dp 里面可能存在多个最优路径,但应把哪一条路径置零,我们无从得知,因而第二次 dp 结果的好坏就依赖于第一次 dp 选择的最优路径是否正确了,此时不满足后无效性,无法使用动态规划。
正确的做法是我们假设两条路径同时行走,因而我们需要记录四个状态,也即两条行程的当前坐标 \((i_1, j_1)\) 与 \((i_2, j_2)\),但是这样空间复杂度很高,我们注意到同时行走会满足 \(i_1 + j_1 = i_2 + j_2 = k\),借助这个关系,我们能够利用 \(k\) 优化去掉一个维度。具体代码如下所示。
#include <bits/stdc++.h>
#include <limits.h>
using namespace std;
#define MAXN 50
int n, r, c, v;
int w[MAXN][MAXN];
int dp[MAXN][MAXN][MAXN];
int main(){
scanf("%d", &n);
while(scanf("%d %d %d", &r, &c, &v), r||c||v) w[r][c] = v;
for(int k = 2; k <= 2 * n; k++){
for(int i1 = 1; i1 <= n; i1++){
for(int i2 = 1; i2 <= n; i2++){
int j1 = k - i1, j2 = k - i2;
if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){
int &y = dp[k][i1][i2]; // 这是一个减少编码量的 trick
int t = w[i1][j1] + (i1 != i2 ? w[i2][j2] : 0);
y = max(y, dp[k - 1][i1 - 1][i2 - 1] + t);
y = max(y, dp[k - 1][i1 - 1][i2] + t);
y = max(y, dp[k - 1][i1][i2 - 1] + t);
y = max(y, dp[k - 1][i1][i2] + t);
}
}
}
}
cout << dp[n + n][n][n] << endl;
return 0;
}
(三)线性规划模型
线性规划模型的两个母题,各是 最长上升子序列(LIS),以及 最长公共子序列(LCS),如果条件允许最好再多记一个 最长公共上升子序列(LCIS),因为 LCIS 确实不太容易临场想出来。
(3.1) 最长上升子序列
最长上升子序列的朴素解法非常符合直觉,代码如下,但是复杂度\(O(N^2)\),通过二分、线段树等方法把复杂度降低,否则数据量较大的时候是无法通过的。
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1005
char a[MAXN], b[MAXN];
int n, m, dp[MAXN][MAXN];
int main(){
scanf("%d %d", &n, &m);
scanf("%s", a + 1);
scanf("%s", b + 1);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(a[i] != b[j]){
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}else{
dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
}
printf("%d\n", dp[n][m]);
return 0;
}
维护单调递增序列 \(g\),并以二分优化的做法是不太符合直觉的,通过这种方法最终栈中剩余的元素个数等于最长上升子序列的长度,但是栈中的字符串并非最长上升子序列。
这种做法其实是一种贪心思想,试想一下,给定一个常量数字 \(N\),以及随机数字 \(x\),显然 \(N\) 越小,满足 \(N < x\) 概率则越大。假设序列 \(s\) 用于存储给定的数组元素,序列 \(g\) 用于存储代表长为 \(i\) 上升子序列的最小结尾字符,也即 \(g[i]\) 代表长度\(i\)上升子序列的末尾元素。我们扫描输入的序列,如果当前元素大于序列末尾元素,则将其插入序列,否则使用当前元素替换第一个小于等于的元素。只要保证长为 \(i\) 上升子序列的结尾字符最小,那么随后能在其尾部接上的字符也就越多。
然而,这种做法丢失了最长上升子序列的具体信息,如果我们想要知道最长上升子序列是哪一条,我们需要另外开设一个数组 \(pos\) 维护信息,\(pos[i]\) 代表第i个元素接在某个上升子序列末尾之后,构成的新上升子序列长度是多少。
#include <bits/stdc++.h>
#include <limits.h>
using namespace std;
void print_LIS_path(vector<int> &s , vector<int> &g, vector<int> &pos){
vector<int> path;
int len = g.size();
for(int i = s.size() - 1; i >= 0 && len; i--){
if(pos[i] == len){
path.push_back(s[i]);
len--;
}
}
// 反过来打印其实就是一条上升子序列了
for(int i = 0; i < path.size(); i++){
printf("%d ", path[i]);
}
printf("\n");
}
int n;
int main(){
scanf("%d", &n);
vector<int> s(n), pos(n), g;
for(int i = 0; i < n; i++){
scanf("%d", &s[i]);
}
// pos 数组存储的是一个长度,代表 第i个 元素能够接在LIS末尾之后构成的上升子序列长度 pos[i]
g.push_back(s[0]);
pos[0] = 1;
for(int i = 1; i < n; i++){
if(s[i] > g.back()){
g.push_back(s[i]);
pos[i] = g.size();
}else{
int t = lower_bound(g.begin(), g.end(), s[i]) - g.begin();
g[t] = s[i];
pos[i] = t + 1;
}
}
printf("%d\n", g.size());
print_LIS_path(s, g, pos); // 打印一条合法的 LIS
return 0;
}
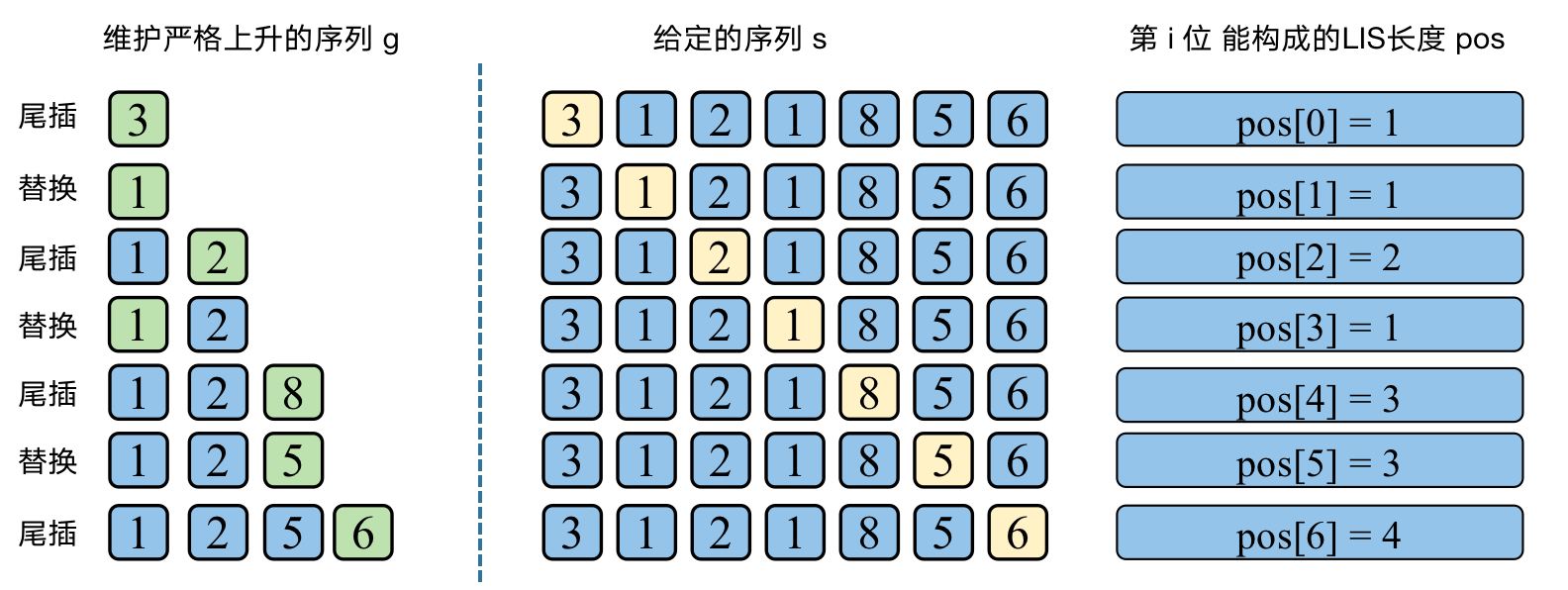
例如,给定样例,\([3,1,2,1,8,5,6]\),每次尾插或替换的时候则更新一下 \(pos\),详细参考下列图例,然后利用 \(pos\) 信息,倒序扫描一趟 \(s\) 即可获取一条合法的 \(\text{LIS}\)。只要保证扫到的 \(pos\) 是单调递减的,则其构成 \(\text{LIS}\) 必然是合法的,因为 \(pos\) 位置是第 \(i\) 个位置可以构成的最长 \(\text{LIS}\) 长度。
(3.2) 最长公共子序列
最长公共子序列也是一个经典的线性规划问题,定义 \(\text{dp[i][j]}\) 代表\(a[1..i]\), \(b[1..m]\) 两个字符串的最长公共子序列,如果我们要对\(a[i]\)、\(b[j]\) 进行分类讨论,如果二者相等,\(\text{dp[i][j] = dp[i-1][j-1]+1}\),如果二者不相等,则分别退一位,取二者中较长的一个,方程 即为 \(\text{dp[i][j] = max\{dp[i-1][j],dp[i][j-1]\}}\),由于两者都退一位的情况已经包含在其中,故不必重复计算。
#include <bits/stdc++.h>
using namespace std;
#define MAXN 1005
char a[MAXN], b[MAXN];
int n, m, dp[MAXN][MAXN];
int main(){
scanf("%d %d", &n, &m);
scanf("%s", a + 1);
scanf("%s", b + 1);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(a[i] != b[j]){
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}else{
dp[i][j] = dp[i - 1][j - 1] + 1;
}
}
}
printf("%d\n", dp[n][m]);
return 0;
}
最长公共子序列的一个变体问题就是编辑距离,例如 AcWing902 最短编辑距离、AcWing899 编辑距离两道题,我们同样要对\(a[i]\)、\(b[j]\)是否相等进行分类讨论,且二者的状态转移方程,形式是类似的。
其状态转移方程 \(\text{dp[i][j]}\) 代表 \(a[1,i]\) 变为 \(b[1,j]\) 所需的最小操作数,我们要对\(a[i]\),\(b[j]\)进行分类讨论,如果二者相等,则有\(\text{dp[i][j]=dp[i-1][j-1]}\),如果二者不相等,那么每一次操作会有增,删,改三种操作,如果需要增加一个字符,说明已经知道如何调整 \(a[1,i]\) 使其变成 \([b,j-1]\),也即知道 \(\text{dp[i][j-1]}\),此时再在 \(a\) 末尾插入一个字符 \(b[j]\)即可。如果需要删除一个字符,说明已经知道如何调整 \(a[1,i-1]\) 使其变成 \(b[1,j]\),也即已经知道\(\text{dp[i][j-1]}\),此时只要删掉\(a[i]\)即可,如果需要修改一个字符,说明已经知道如何调整 \(a[1,i-1]\) 使其等于 \(b[1,j]\),此时只要\(a[i]\) 变为 \(b[j]\) 即可,具体代码如下所示。
int edit_distence(char a[], char b[]){
int n = strlen(a + 1), m = strlen(b + 1);
for(int i = 1; i <= n; i++) dp[i][0] = i;
for(int j = 1; j <= m; j++) dp[0][j] = j;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(a[i] == b[j]){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
}
}
return dp[n][m];
}
(3.3) 最长公共上升子序列
Waiting...
(四)区间规划模型
Waiting...
(五)状态压缩动规模型
Waiting...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号