#matplotilib#3D绘图

mport numpy as np
import matplotlib.pyplot as plt
from  mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
#创建3d绘图区域
ax = plt.axes(projection='3d')

plt.show()

 

 

 

 

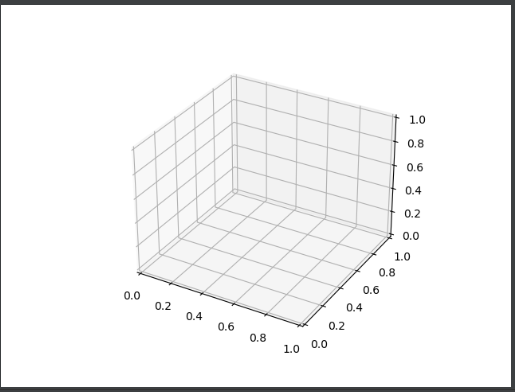
(1)mpl_toolkits.mplot3d，通过调用该程序包一些接口可以绘制 3D散点图、3D曲面图、3D线框图等。

首先创建一个三维绘图区域， plt.axes() 函数提供了一个参数projection，将其参数值设置为 "3d"。如上图所示。

(2)

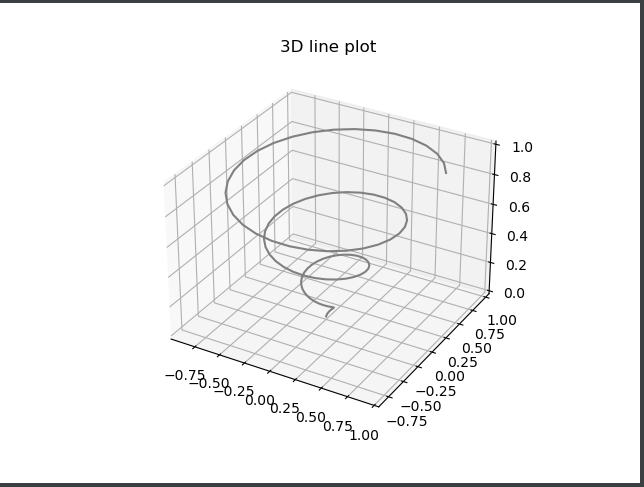
import numpy as np
import matplotlib.pyplot as plt
from  mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = plt.axes(projection='3d')
#从三个维度构建
z = np.linspace(0, 1, 100)
x = z * np.sin(20 * z)
y = z * np.cos(20 * z)

#调用 ax.plot3D创建三维线图
ax.plot3D(x, y, z, 'gray')
ax.set_title('3D line plot')

plt.show()

 

 

 

 

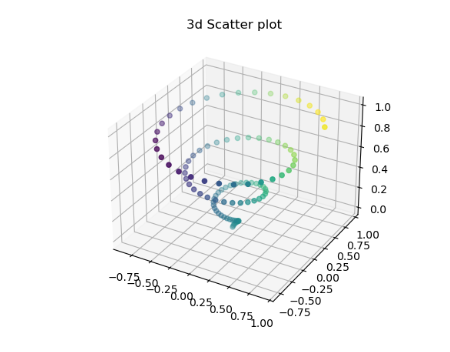
3D散点图

from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
#创建绘图区域
ax = plt.axes(projection='3d')
#构建xyz
z = np.linspace(0, 1, 100)
x = z * np.sin(20 * z)
y = z * np.cos(20 * z)
c = x + y
ax.scatter3D(x, y, z, c=c)
ax.set_title('3d Scatter plot')
plt.show()

 

 

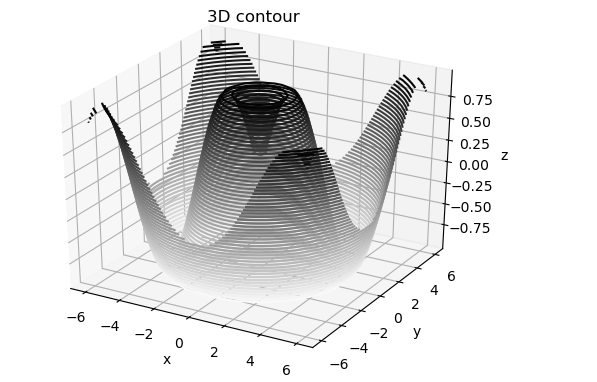
3D等高线图

from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
   return np.sin(np.sqrt(x ** 2 + y ** 2))
#构建x、y数据
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
#将数据网格化处理
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
#50表示在z轴方向等高线的高度层级，binary颜色从白色变成黑色
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('3D contour')
plt.show()

 

 

3D曲面图

from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
#求向量积(outer()方法又称外积)
x = np.outer(np.linspace(-2, 2, 30), np.ones(30))
#矩阵转置
y = x.copy().T 
#数据z
z = np.cos(x ** 2 + y ** 2)
#绘制曲面图
fig = plt.figure()
ax = plt.axes(projection='3d')
调用plot_surface()函数
ax.plot_surface(x, y, z,cmap='viridis', edgecolor='none')
ax.set_title('Surface plot')
plt.show()

曲面图表示一个指定的因变量y与两个自变量x和z之间的函数关系。

3D 曲面图是一个三维图形，它非常类似于线框图。不同之处在于，线框图的每个面都由多边形填充而成。Matplotlib 提供的 plot_surface() 函数可以绘制 3D 曲面图，该函数需要接受三个参数值 x，y 和 z 。