#指数加权平均#

公式：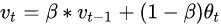

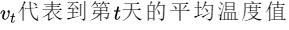
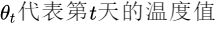
公式意思就是前一日的V值乘β倍加上当日温度的(1-β)倍,如果用红线表示这个计算数值的话就可以得到每日温度的指数加权平均值.

(一年中开头和结尾气温较低，中间气温较高，整体趋势是这样的，但是噪声很大。下图蓝点表示离散的每天温度)

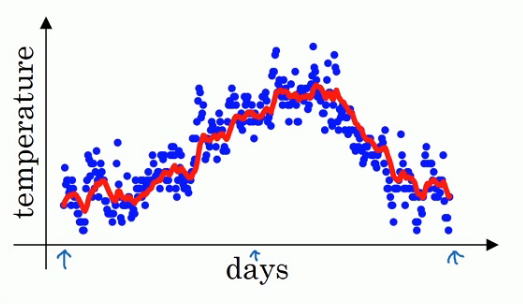
你可以将其认为该数值表示的是1/(1-β)天的平均值,例如如果这里取β是取0.9,那么这个V值表示的是十天以来的温度的加权平均值.如果我们设置β值是0.98那么我们就是在计算50天内的指数加权平均,这时我们用图中的绿线表示指数加权平均值.黄色的β值是0.5。

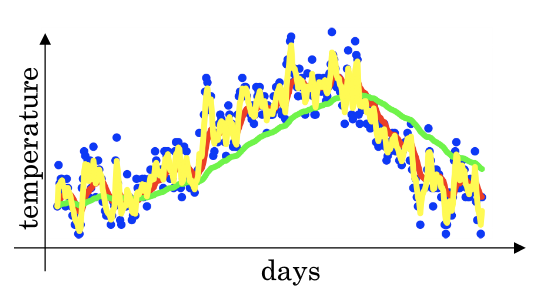
可以看到绿线会更加平缓，波动更小。绿线的意义是0.98权值给了之前的值，0.02给了今天的.

$v$

将 ③ 式代入 ② 式，再将 ② 式代入 ① 式可以得到

从这个式子中可以发现，运用指数加权平均后，第 100 天的温度受到了前面所有天温度的影响，随着向前的天数减小，影响也减小，总之，这就使得处理后的数据更加平滑，噪声更少。

但是为什么说 β = 0.9 时，这里的 v ₁₀₀是对前 10 天气温平均值的粗略计算呢？

(这里的含义就是假如我们计算第100天且β等于0.9，在我们计算时，由于seita前面的0.9的幂次，如果到10次则约等于0.34。我们遵循的规律是，只要β接近1，就会有个数1-β等于0，使得系数为β ^1/1-β的值约等于0.37，0.37以及更小的系数可以忽略不记，所以系数为 β^1/1-β以及之后系数代表的可以忽略，所以我们计算的就是seita100、99...91这十天的平均温度。)

posted @ 2021-09-24 18:07 tanyayangyang 阅读(148) 评论(0) 收藏举报

刷新页面返回顶部

tanyayangyang

#指数加权平均#

公告