做题笔记（2025.11至）

11.4

CF436E

\(n\) 个关卡，每个关卡可以打 \(1\) 颗星或 \(2\) 颗星，消耗的时间分别是 \(a_i\) 和 \(b_i(a_i<b_i)\)。至少要集齐 \(w\) 颗星，求最小的时间。

反悔贪心。一共有 \(4\) 种情况。

• 选一个没打过的关卡，打一颗星，花费 \(a_i\)。
• 选一个打了一颗星的关卡，再打一颗心，花费 \(b_i-a_i\)。
• 选一个打了一颗星的关卡 \(i\) 和一个没有打的关卡 \(j\)，不选 \(i\)，\(j\) 两个都选，花费 \(b_j-a_i\)。
• 选一个打了两颗星的关卡 \(i\) 和一个没有打的关卡 \(j\)，不选 \(i\) 的第二颗，\(j\) 两个都选，花费 \(a_i+b_j-b_i\)。

综上，\(5\) 个小根堆分别维护 \(a_i\)，\(b_i-a_i\)，\(a_i-b_i\)，\(b_i\)，\(-a_i\)。
然后乱搞。

11.7

P2237

题面

首先有一个转化：每一个 \(CE(a,b)\) 视为 \(b\) 向 \(a\) 连一条边权为 \(i\) 的边。每个点只能走边权最小的出边。走的边权只能递增。若每个节点都能到 \(1\)，且随机删掉一条边之后所有节点依旧能到 \(1\)，则可行。
明确一点：加的边只会是 \((1,i)\) 的形式。
好把题目过于神秘，不会了。

11.10

P3193

有多少种长度为 \(n\) 的数字串满足给定的长度为 \(m\) 的字符串不是它的字串。\(n\leq 10^9,m\leq 20\)。

定义 \(f_{i,j}\) 表示长串匹配到第 \(i\) 位，短串匹配到第 \(j\) 位的方案数。答案为 \(\sum_{i=0}^{m-1}f_{n,i}\)。
转移 \(f_{i,j}=\sum_{k=0}^9 f_{i-1,p}\)（ \(k\) 是将要加入的数字）。
\(p\) 的值并不确定，有如下三种可能：

• 匹配了，\(p=j-1\)。
• 完全失配，\(p=0\)。
• 匹配了短串的某一个前缀。

让我们考虑另一种转移方式：

\[f_{i,j}=\sum_{k=0}^{m-1} f_{i-1,k}\times g_{k,j} \]

其中 \(g_{k,j}\) 表示将匹配 \(k\) 个变成匹配 \(j\) 个的方案数。
由于短串已知，所以 \(g\) 可以预处理。此时复杂度已经来到了 \(O(m^2n)\)。

这个东西可以矩阵。

11.15

P3607

一个序列，可以反转一个子序列，求反转后的最长不下降子序列长度。\(n\leq 50,a_i\in[1,50]\)。

反转的子序列长度一定是一个偶数，并且一定单调不增。
考虑区间dp（别问怎么想到的），应该有两类转移：

• 不改变反转的子序列。
• 在当前选定的要反转的子序列的头和尾各加一个数，满足依旧单调不增。

为了在加数后保证单调性，我们需要记录区间的值域。
令 \(f_{l,r,L,R}\) 表示 \([l,r]\) 的区间，值域为 \([L,R]\) ，最大不降子序列的长度。
在不反转的情况下，有如下三种转移方程：

• 继承：\(f_{l,r,L,R}=\max(f_{l,r,L+1,R},f_{l,r,L,R-1})\)
• 从 \([l+1,r]\) 转移：\(f_{l,r,L,R}=\max(f_{l,r,L,R},f_{l+1,r,L,R}+[a_l=L])\)
• 从 \([l,r-1]\) 转移：\(f_{l,r,L,R}=\max(f_{l,r,L,R},f_{l,r-1,L,R}+[a_r=R])\)

修改反转区间：

• \(f_{l,r,L,R}=\max(f_{l,r,L,R},f_{l+1,r-1,L,R}+[a_l=R]+[a_r=L])\)

答案 \(f_{1,n,1,50}\)。

P2292

给定 \(n\) 个模式串 \(s\) 和 \(m\) 个主串 \(t\)，对于每一个 \(t\)，请求出其最长的前缀，满足该前缀是由若干模式串（可以多次使用）首尾拼接而成的。\(1\leq n\leq20，1\leq m\leq50，1\leq |s|\leq10，1\leq |t|\leq10^6\)

令主串 \(t\) 匹配到第 \(i\) 位，当前在 AC 自动机上 \(u\) 号点。对于 fail 树上 \(u\) 的一个祖先 \(v\)，若他是终止结点，则主串 \(t\) 长度为 \(i\) 的前缀有一个长度为 \(dep_v\) 的后缀。
定义 \(f_i\) 表示长度为 \(i\) 的前缀是否可以拼成。

\[f_i=or_{v是u的祖先且v是终止结点}\{f_{i-dep_v+1}\} \]

复杂度 \(O(m|s||t|)\)。
注意到 \(dep_v\leq 20\)。令状压数组 \(g_u\) 的第 \(i\) 位表示 \(u\) 的祖先中有一个深度为 \(i\) 的终止结点。

\[g_u=g_{fa_u}+(2^{dep_u}+[u是终止结点]) \]

在匹配 \(t\) 串的同时，定义 \(x\) 的第 \(j(j\leq 20)\) 位 \(=f_{i-j}\)。若 \(x \operatorname{or} g_u\) 不为 \(0\)，\(f_i=1\)。

11.18

P9196

给定 \(n\) 个模式串 \(S\)，\(m\) 个询问，每组查询包含两个字符串 \(P\)，\(Q\)，试求：有多少个模式串同时存在前缀 \(P\) 和后缀 \(Q\)。\(|\sum| =4,n,m\leq 10^5,\sum|S|,\sum |P|,\sum |Q|\leq 2\times 10^6\)。

把 \(S\) 变成 \(S+\) '#' \(+S\)，只需判断 \(Q+\) '#' \(+P\) 是否是 \(S\) 的字串即可。
AC自动机。

11.20

P6155

有一个长度为 \(n\) 的数组 \(a\)，每次选中其中的一个元素 \(a_i\) 使其 \(+1\)，花费为 \(b_i\)。可以自由排列 \(b\) 的元素，求最小花费。\(n\leq 10^6,a_i,b_i\leq 10^9\)。

考虑用一个队列模拟以上操作：枚举 \(x\) 表示值域，将所有 \(a_i=x\) 的 \(a_i\) 加入队列。然后取出队头 \(head\) 表示将 \(x\) 这个值分配给 \(head\)，\(head\) 的修改次数即为 \(x-a_{head}\)。按修改次数排序后与 \(b\) 匹配求出答案。

这个算法并不正确。假设队列中存在两个元素 \(s,t(s<t)\)，以上算法的答案是 \((x-s)\times b_2+(x+1-t)\times b_1=x(b_1+b_2)+b_1-s\times b_2-t \times b_1\) （假设 \(b_1<b_2\)）。如果我们选择将 \(x\) 分配给 \(t\)，答案为 \((x-t)\times b_2+(x+1-s)\times b_1=x(b_1+b_2)+b_1-t\times b_2-s\times b_1\)。因为 \(t\times b_2+s\times b_1 \geq s\times b_2+t\times b_1\)，所以将 \(x\) 分配给队内最大值最优。把队列改成栈。此时复杂度 \(O(n \log n + max\{ a_i\})\)。

加入一个小优化：若不存在 \(i\) 使得 \(a_i=x\)，将 \(x\) 跳到大于 \(x\) 的最小的 \(a_i\) 的值。

11.24

P14363

终于想起来补 CSP-S T3了。

最不长脑子的做法：令 \(s_1=ABC,s_2=ADC\)，把他们变成 \(A+\#+BD+\#+C\) 的形式插入AC自动机。\(t\) 串也是一样的操作。理论上，本题询问时需要在 \(fail\) 树上做奇异操作。但是暴力统计能过。

11.25

P6088

一棵树，边权是一个长度不大于 \(10\) 的字符串，每次询问给定两个节点 \(u,v\) 和一个字符串 \(S\)，统计 \(u\) 到 \(v\) 的路径上有多少个字符串以 \(S\) 为前缀。

根据以往的经验，令 \(num_u\) 表示 \(1\) 到 \(u\) 的路径的答案，则 \(ans=num_u+num_v-2\times num_{LCA(u,v)}\)。计算 \(num_u\) 可以可持久化trie。

12.1

P3215

体面很长

一个简单的转换:令 (\(=-1\)，)\(=1\)，然后 \(ans\) 就等于 \(\left\lceil\dfrac{premax}{2}\right\rceil+\left\lceil\dfrac{|sufmin|}{2}\right\rceil\)。
分析一下有哪些要点：
1、节点需要维护哪些信息？
\(prmax,prmin,sfmax,sfmin\)，还有平衡树必备的几个信息。
2、需要维护那些标记？
题目中给出的三个 \(tag\)。
3、如何维护信息？
先确定三个 \(tag\) 的优先级：\(invert>cover>swap\)
取反时，\(key,sum,cover\) 直接取反，\(prmax,prmin\) 交换后取反，后缀同理。
覆盖时，若覆盖的值是正数，\(prmin,sfmin\) 为 \(0\)。若是负数，\(prmax,sfmax\) 为 \(0\)。
交换时，直接交换 \(prmax,sfmax\) 和 \(prmin,sfmin\)。
4、如何修改？
直接拆出来打标记。
5、如何合并？

tr[p].prmin=min(tr[tr[p].l].prmin,tr[tr[p].l].sum+tr[p].key+tr[tr[p].r].prmin);
tr[p].prmax=max(tr[tr[p].l].prmax,tr[tr[p].l].sum+tr[p].key+tr[tr[p].r].prmax);
tr[p].sfmin=min(tr[tr[p].r].sfmin,tr[tr[p].r].sum+tr[p].key+tr[tr[p].l].sfmin);
tr[p].sfmax=max(tr[tr[p].r].sfmax,tr[tr[p].r].sum+tr[p].key+tr[tr[p].l].sfmax);

冲锋即可。

12.5

SP11470

区间加、历史区间和。\(1\leq n,m\leq 2\times 10^5\)。

考虑如何在可持久化线段树上打lazy tag。
遍历树并找到需要打标记的点并不难，难点是如何在有限的空间内处理询问。
方案1：只有当pushdown到了这个点时才把点建出来。
方案2：标记永久化。我们始终不下传lazy tag，当我们统计完了子节点的答案后加上lazy tag的影响。

P3402

可持久化并查集。

把 \(fa_u\) 和 \(sz_u\) 变成可持久化数组。

P3168

给定 \(m\) 个区间，每个区间有一个权值，\(n\) 个询问，每次给出一个点 \(x\) 和 一个 \(k\)，求所有覆盖了点 \(x\) 的区间中，权值前 \(k\) 小的权值和。\(n,m\leq 2\times 10^5\)。

差分。对，对主席树差分。对，英改师，就这样，就没了？

12.6

CF935F

题面

分三种情况讨论 \(a_i\) 的贡献：

• \(a_{i-1},a_{i+1}\leq a_i\)
  
  贡献显然是 \(2x\)。

• \(a_{i-1}\leq a_i\leq a_{i+1}\) 或 \(a_{i+1}\leq a_i\leq a_{i-1}\)
  
  贡献为 \(x+a_i+x-a_{i-1}-(a_{i-1}-a_i)=2x-2(a_{i-1}-a_i)\)。

• \(a_{i-1},a_{i+1}\geq a_i\)
  
  贡献为 \(2x-2(a_{i-1}-a_i)-2(a_{i+1}-a_i)\)。

以上三种情况合并起来，可以写出表达式 \(2x-2(max(a_{i-1}-a_i,0)+max(a_{i+1}-a_i,0))\)，我们只需要维护区间 \([l,r]\) 中 \(max(a_{i-1}-a_i,0)+max(a_{i+1}-a_i,0)\) 的最小值。
令 \(b_i=a_{i+1}-a_i\)。维护 \(min\{max(-b_{i-1},0)+max(b_i,0)\}\)，区间修改可以差分。
\(l=r\) 要特判。\(l=1,r=n\) 也要特判。

12.15

补前一周没写的笔记。

CF1858E2

一个数组，支持以下操作：
+x 将整数 \(x\) 添加到数组 \(a\) 的末尾。
-k 从数组 \(a\) 中删除最后的 \(k\) 个数字。
! 撤销上次更改。只有前两种类型的查询（+ 和 -）才被视为更改。
? 求数组 \(a\) 中不同数字的个数。

定义 \(a\) 表示 \(i\) 位置最后一次修改时的值，\(l\) 表示当前数组长。

对于添加操作，维护值域个 set 表示每个值出现的位置。类似 HH的项链，每个数出现的第一个位置在树状数组上为 \(1\)。
注意 \(x\) 之前出现的最小位置可能在 \(l\) 之后，要先修改树状数组上该位置的值。
对于删除操作，\(l \leftarrow l-k\)。

维护一个栈保存这两个操作，注意添加操作保留 \(a_l\) 原本的值。

对于查询，直接输出前缀和。

对于撤销，暴力地还原。

CF266E

-区间覆盖
-求 \(\sum_{i=l}^r a_i\times (i-l+1)^k\)，\(0\leq k\leq 5\)。

拆式子。根据二项式定理，

\[\begin{aligned} &\sum_{i=l}^r a_i\times (i-l+1)^k \\=&\sum_{i=l}^r a_i\times \sum_{j=0}^k i^j(1-l)^{k-j}\binom{k}{j} \\=&\sum_{j=0}^k(\sum_{i=l}^r a_i\times i^j)\times (1-l)^{k-j}\binom{k}{j} \end{aligned}\]

开 \(6\) 棵线段树维护 \(\sum_{i=l}^r a_i\times i^j\)，后边的可以预处理。
区间推平操作可以预处理 \(\sum_{i=1}^n i^j\)，在 \(O(1)\) 时间内知道修改后的值。

12.16

CF702F

题面

对询问建立平衡树，对体恤衫排序。对于每个体恤衫，把树分成三份：

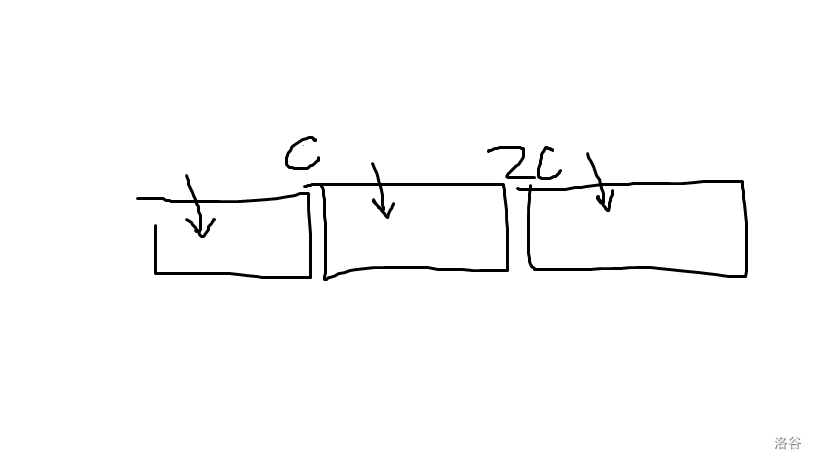
\(< c\) 的，不会买这个T恤。
\([c,2c)\) 的，打一个群体减 \(c\) 的 \(tag\)，拆散暴力加入第一颗。
\(\geq 2c\) 的，打一个群体减 \(c\) 的 \(tag\)，树中元素相对位置不会改变。
再把三棵树拼起来。

12.18

CF1326E

阅读理解挑战

简化题意：每次激活一个炸弹，然后按顺序将每一个炸弹加入一个集合，若该炸弹已被激活，弹出集合中的最大元素。求最后集合中的最大元素。

观察样例，发现答案单调不增。证明显然。
考虑答案 \(x\) 在什么情况下不减：存在一个后缀，令 \(q\) 表示后缀中 \(\geq x\) 的数的个数，\(p\) 表示后缀中激活的炸弹数，只要满足 \(q>p\)，\(x\) 就不减。

线段树维护每一个以 \(i\) 开头的后缀的 \(q-p\)。激活一个炸弹时，对于个前缀做区间减。若不存在满足条件的后缀，令 \(x\leftarrow x-1\)，对一个前缀做区间加。

12.19

ABC255H

一个长为 \(n\) 的序列 \(a\)，每天 \(a_i\) 会变成 \(a_i+i\)。询问第 \(d_i\) 天，求区间 \([l,r]\) 的和，然后将 \([l,r]\) 赋值为 \(0\)。
\(n\leq 10^{18}，0<d_1<d_2\dots<d_n\leq 10^{18}，1\leq l\leq r\leq n\)。

动态开点，标记当前节点经历了 \(tag\) 天和是否被赋值 \(tag2\)。单纯的难写。

12.22

P12747

题面

定义每个点点权为度数 \(-2\)，答案为树上点权最大的一条路径的点权和 \(-2\)。
类比树的直径。定义 \(f_u\) 表示 \(u\) 的答案，\(d_u\) 表示 \(u\) 为起点的向下的单链的最大点权。
递归时先处理 \(f\)，再处理 \(d\)。

12.27

CF1638E

题面

首先，对于所有某颜色的元素的 \(add\) 操作可以对每种颜色统计总偏移量。然后，不难发现线段树上颜色相同的一段可以一起改，不需要往下递归。并且区间覆盖的操作使得每次修改最多只会增加 \(2\) 个颜色段，所以复杂度正确。

P4344

题面

操作 \(0\) 和 \(2\) 都很好实现，操作 \(1\) 套一个二分就行了。

12.30

CF809D

题面

先想暴力 DP。令 \(f_i\) 表示长度为 \(i\) 的最长上升子序列的最后一位。有三种转移：

• \(f_i<l\)，\(f_i=min\{f_i,l\}\)
• \(l\leq f_{i-1}<r\)，\(f_i=min(f_{i-1}+1,f_i)\)
• \(f_{i-1}\geq r\)，\(f_i=f_i\)

建立一颗平衡树表示数组 \(f\)。平衡树有序。对于第一种转移，插入一个 \(l\) 代表更新了 \(f_i\)。对于第二种转移，将键值为 \([l,r)\) 的子树集体后移一位并 \(+1\)。由于插入了一个 \(l\)，后移可以不做。对于第三种转移，删除第一个 \(\geq r\) 的节点。答案即为平衡树大小。

1.2

P5236

题面

点双令人不适的地方在于一个点可能属于多个点双，导致不能向强连通分量一样缩点。但我们很多时候希望将无向图变成树的形态，所以有了圆方树。
由于一个点可能属于多个点双，我们考虑将点双视作一个方点，每个点与其所属的方点建边的方式建立关系。如图：

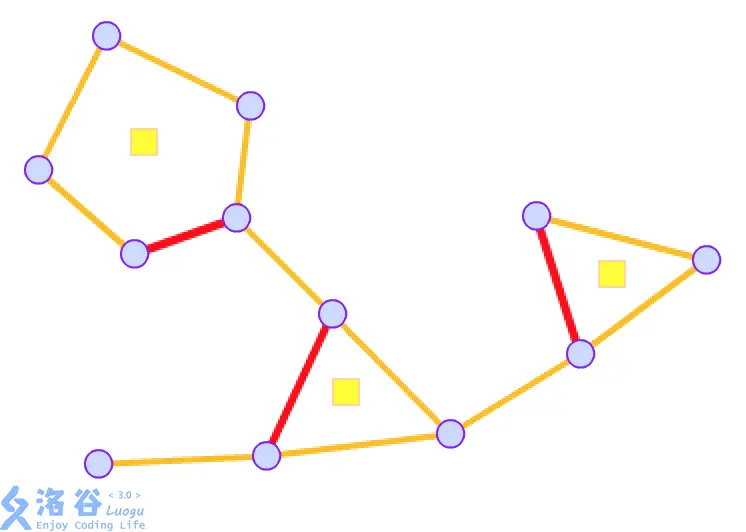
方点代表点双。

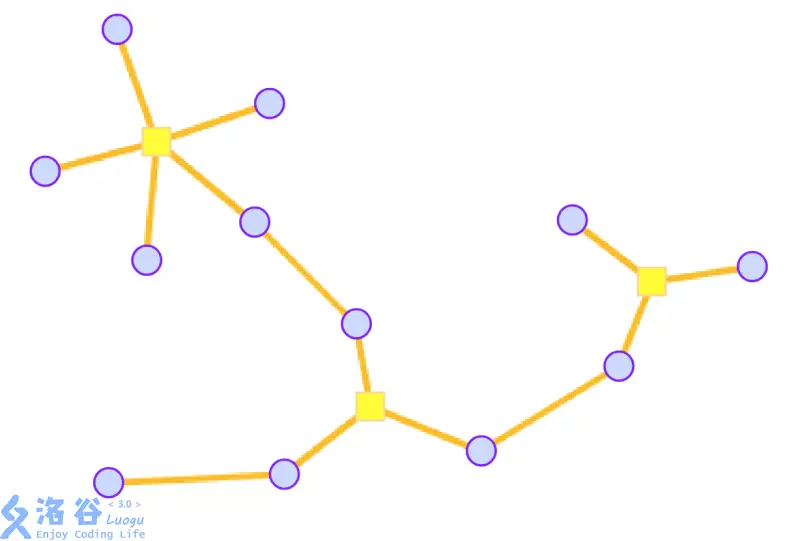
然后就可以做树上操作了。
具体实现时，开一个栈维护 \(dfs\) 的路径上的点，遇到一条返祖边就 \(pop\) 掉环中的所有点，并与代表该点双的方点建边。注意不能 \(pop\) 割点。

对于本题，在 \(pop\) 时维护到割点的两条路径的长度，取较小的为到方点的边权。方点到父亲无边权。若 \(LCA\) 是方点，就取两个儿子，计算到割点的距离差。

CF487E

题面

套一个树剖即可。

P9320

题面

在 CF1638E 的基础上加一个 LCA。

1.3

P4630

给定一张简单无向图，问有多少对三元组 \(<s,c,f>\) （互不相同）使得存在一条简单路径从 \(s\) 出发，经过 \(c\) 到达 \(f\) 。

若 \(s,f\) 已确定，则 \(c\) 的数量是 \(s\) 到 \(f\) 所有简单路径的并 \(-2\)。
引理：\(s\) 到 \(f\) 所有简单路径的并是 \(s\) 到 \(f\) 所有点双的并。

证明：
首先，\(s\) 到 \(f\) 所经过的点双是确定的，且对于每个点双，一定是从一个固定点入，另一个固定点出。
只需要证一个点双中任意三点 \(a,b,c\) 必然有路径 \(a\to b\to c\)。
考虑单环的情况。\(a,c\) 将环分成了两部分。此时，\(b\) 无论在哪边，都存在简单路径满足情况。其他构型的点双连通性只会更强。
实现：一条路径上点双的并的大小等于点双的大小和减去割点数量。将方点的点权定为点双的大小，圆点的点权为 \(-1\)，等价于求树上任意两点路径的点权和。

1.5

P5906

询问区间 \([l,r]\) 内两个相同的值的最远距离。

线段树没法做，分块不想打，考虑莫队。
加入很简单，但删除没法搞，考虑回滚莫队。
考察左端点在同一块的询问的性质：
左端点的单次移动一定不超过 \(O(\sqrt{n})\),右端点总移动次数为 \(O(n)\)，且只会加入。
考虑以这个块的右端点为界限分成两块。右边的答案可以在上一次的基础上加若干元素。左边的开一个临时数组统计答案，算完之后直接清除。如果 \([l,r]\) 在同一块，直接暴力。
不难发现是 \(O(n\sqrt{n})\) 的。

对于本题，数组 \(st_i\) 表示 \(i\) 首次出现的位置，\(ed_i\) 表示 \(i\) 在 \([当前块右端点,r]\) 最后一次出现位置。\(ed2_i\) 表示 \(i\) 在 \([l,当前块右端点]\) 最后一次出现位置。左端点移动时更新 \(ed2\)，并且与 \(ed\) 取 \(max\)。

1.10

P4074

题面

在序列上可以莫队做。考虑把树上操作变成序列操做。
\(dfs\) 是一个想法，但会多算路径上节点的其他子树的贡献。考虑这样的 \(dfs\) 序：进入和离开一个点时，将其加入序列。这样，路径 \(u\to v\) 上的点（除 \(lca\)）只会出现一次，其他不在路径上的点会出现 \(0\) 或 \(2\) 次。于是在莫队时记录每个节点的经过次数，以此决定时增加还是删除。注意要补上 \(lca\) 的贡献。

P4887

题面

莫队二次离线。注意到莫队有时候无法快速的转移 \(l\) 和 \(r\) 指针，本质上是无法快速获得 \(l\) 或 \(r\) 变动后的偏移量。
记指针移动一次的偏移量与指针的函数关系为 \(f(x,l,r)\)，表示新加入下标 \(x\) 的元素，对区间 \([l,r]\) 的贡献。令 \(f(x,l,r)=f(x,1,r)-f(x,1,l-1)\)，其中 \(f(x,1,r)\) 可以预处理，把 \(f(x,1,l-1)\) 开一个 vector 存下来，之后扫描线求答案。
这样时空复杂度都是是 \(O(n\sqrt{m})\)，考虑优化。
注意到每次移动指针都会存一个询问，考虑把指针的一连串移动存在一起。令 \(r\) 表示指针当前位置，\(r'\) 表示指针目标位置。则在 \(l-1\) 的 vector 中存下 \([r,r']\) 这个询问区间。
对于本题，把 \([0,2^{14}]\) 内所有 \(popcount\) 为 \(k\) 的数存下来，开一个桶 \(cnt_i\) 表示 \(popcount(i\oplus x)=k\) 的 \(x\) 个数。加入 \(a_i\) 时，遍历所有\(popcount\) 为 \(k\) 的数 \(x\)，令 \(cnt_{a_i \oplus x}++\)。\(f(r+1,1,r)=cnt_{a_{r+1}}\)。

1.16

P5501

题面

每加入一个整数 \(a_{r+1}=x\)，会对答案产生三部分的贡献：[l,r]内所有小于 \(x\) 的数的个数 \(\times x\)+大于 \(x\) 的数的和 \(+x\) 自身。令前两种贡献的答案为函数 \(f(r+1,l,r)=f(r+1,1,r)-f(r+1,1,l-1)\)，其中 \(f(r+1,1,r)\) 可以用值域分块预处理，\(f(r+1,1,l-1)\) 离线下来。
分块这样写：对于每个值和整块，维护它的排名 \(cnt\) 与比它大的数的和 \(sum\)。当加入一个 \(x\) 时，编号 \([blo[x+1]+1，tot]\) 的块 \(cnt+1\)，编号 \([1,blo[x-1]-1]\) 的块 \(sum+x\)，散块暴力处理。
注意不要忘记 \(r+1\) 自身的贡献。