位姿，地图，路径曲线和计算几何知识

位姿变换；

地图操作；

路径，曲线和速度规划速度平滑；

计算几何；cgal,gems;

 

polygon_test 测试多边形功能

多边形offset Inward/outward 向内外偏移，路径向内外偏移（todo：QtCode测试）

E:\[OPENSOURCE_CODE]\grid_map-master\grid_map_core\src\Polygon.cpp

bool Polygon::offsetInward(const double margin)
{
// Create a list of indices of the neighbours of each vertex.
// TODO: Assuming counter-clockwise ordered convex polygon.
std::vector<Eigen::Array2i> neighbourIndices;
const unsigned int n = nVertices();
neighbourIndices.resize(n);
for (unsigned int i = 0; i < n; ++i) {
neighbourIndices[i] << (i > 0 ? (i-1)%n : n-1), (i + 1) % n;
}

std::vector<Position> copy(vertices_);
for (unsigned int i = 0; i < neighbourIndices.size(); ++i) {
Eigen::Vector2d v1 = vertices_[neighbourIndices[i](0)] - vertices_[i];
Eigen::Vector2d v2 = vertices_[neighbourIndices[i](1)] - vertices_[i];
v1.normalize();
v2.normalize();
const double angle = acos(v1.dot(v2));
copy[i] += margin / sin(angle) * (v1 + v2);
}
vertices_ = copy;
return true;
}

　　

多边形相关code Qt测试

参考开源项目E:\[OPENSOURCE_CODE]\grid_map-master\grid_map_core\src\Polygon.cpp

E:\QtCode\cleanPackTest\main\polygon_test

 

 

 

 

 

 

 

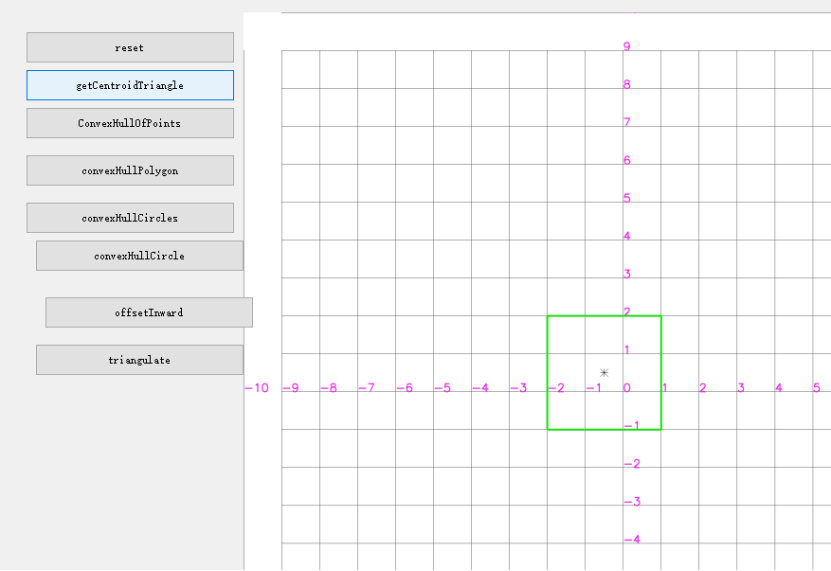
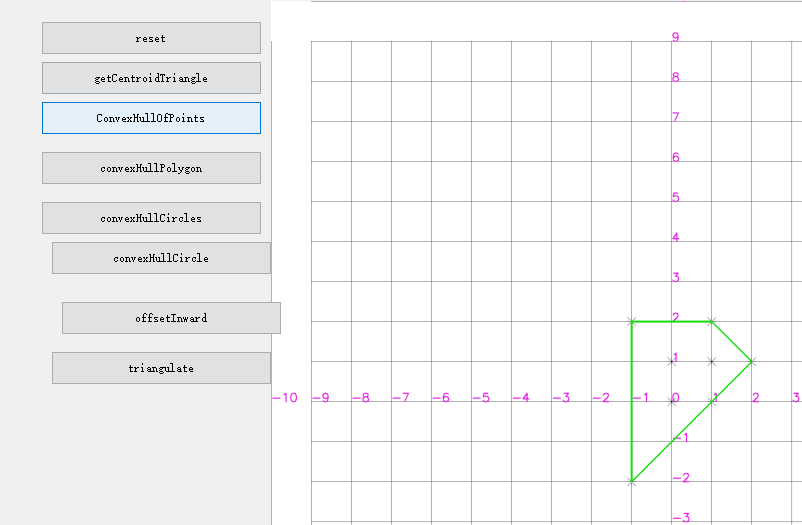
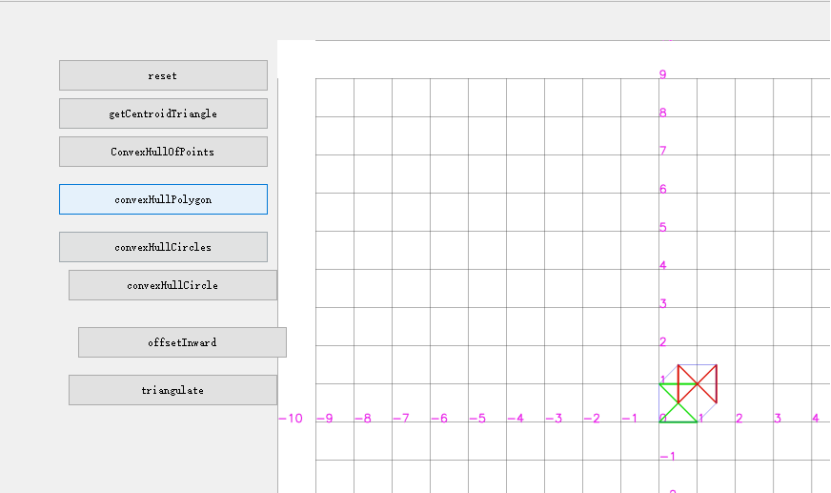
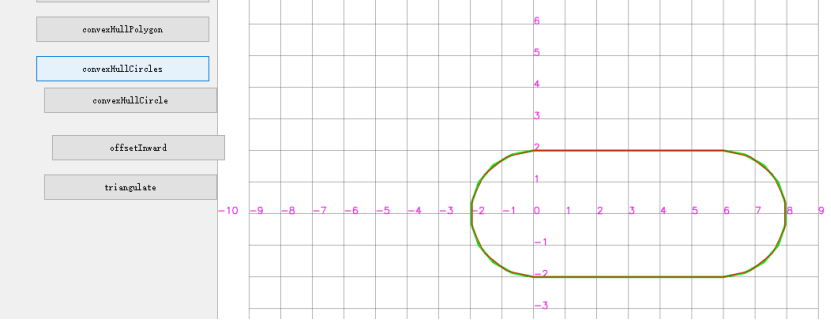
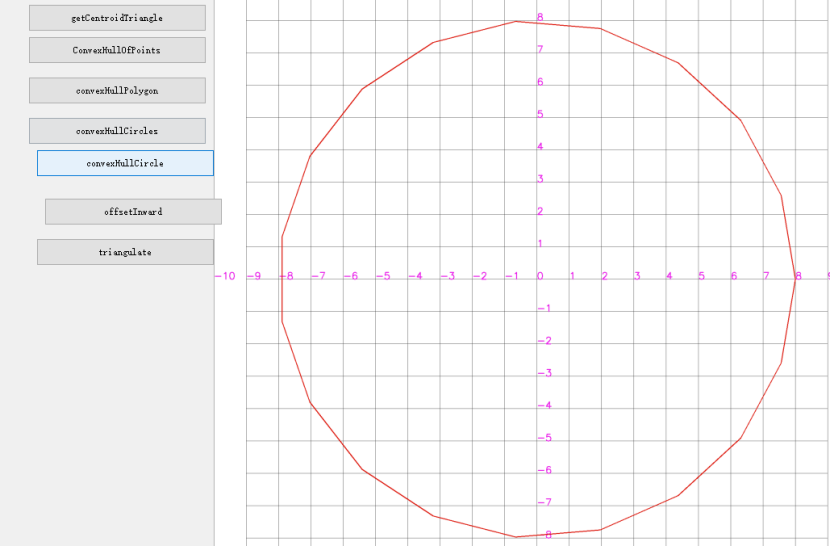
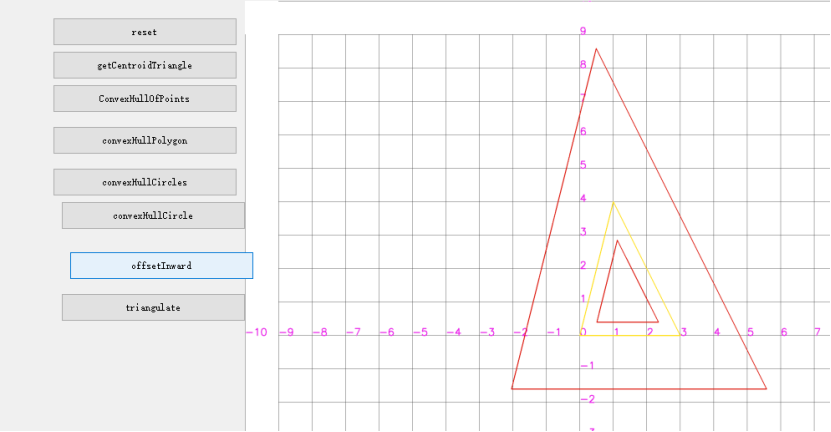
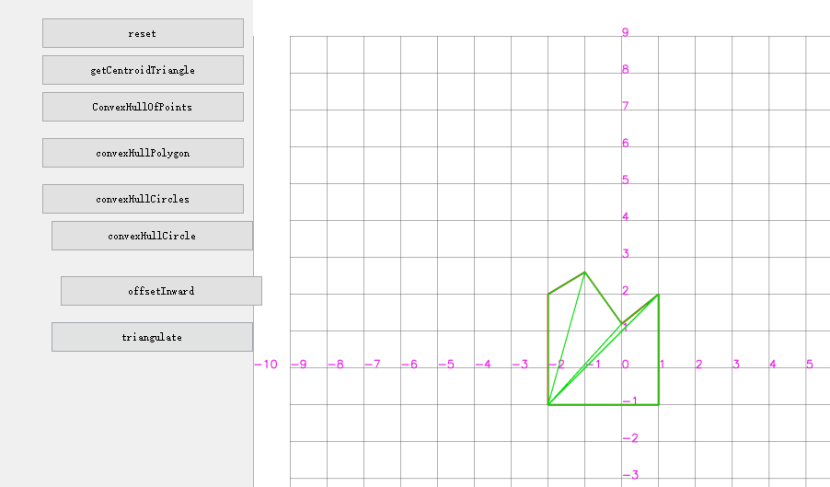
测试bresenham画圆，连接原点到圆形点可以覆盖所有格点；

见笔记记录6

E:\QtCode\cleanPackTest\main\polygon_test\mainwindow.cpp

 

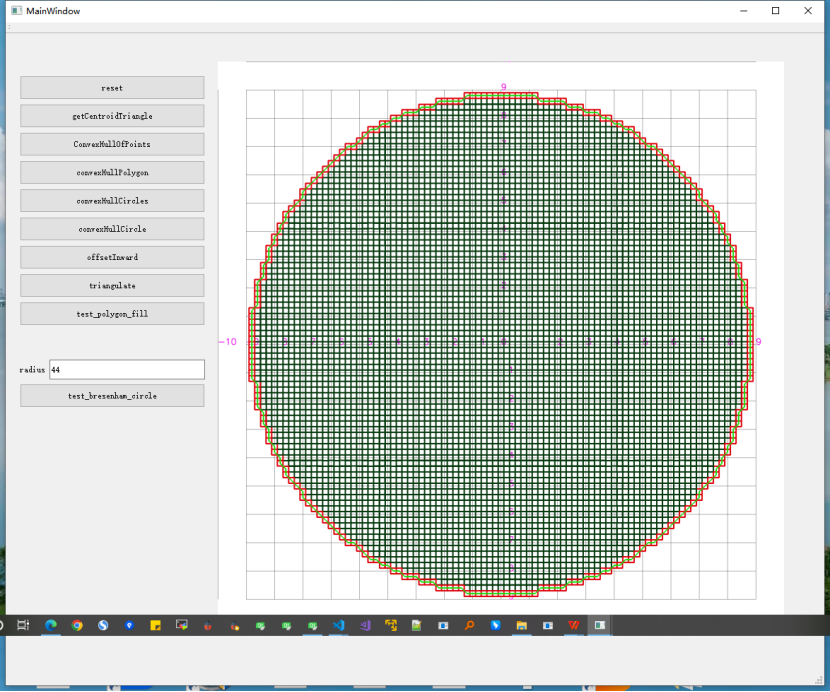
test_polyon_utils

circle points num:2831

line_points_max:501

linePointsMaxPoint:(0,0)

像素半径为500时候，圆周上的点个数为2831，射线上的点个数最大为500；

 

计算机器外轮廓的近似多边形，用于碰撞检测

 

 

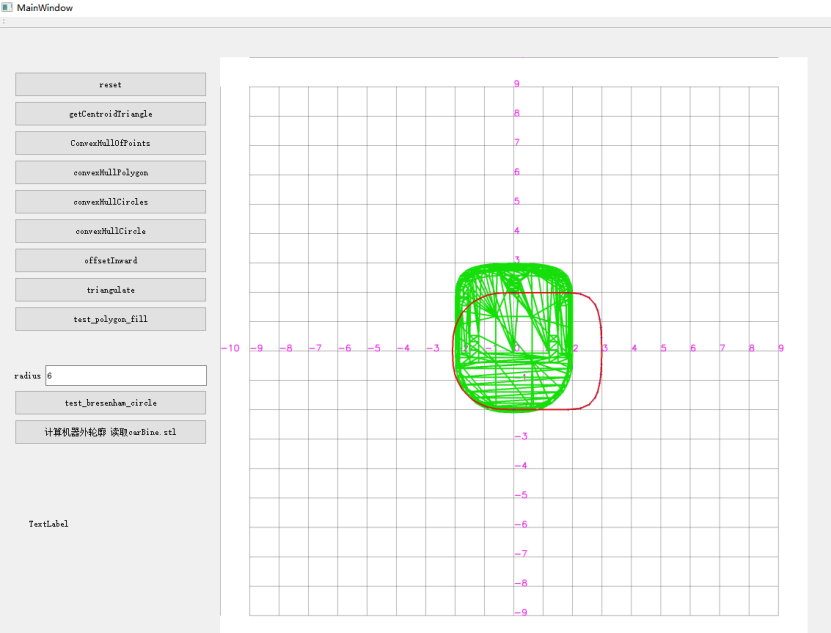
E:\QtCode\cleanPackTest\main\polygon_test\mainwindow.cpp

0 , 2
1.846 , 1.99616
2.26201 , 1.95555
2.56436 , 1.82419
2.76865 , 1.59086
2.8541 , 1.39529
2.92767 , 1.0924
2.96419 , 0.809724
2.98696 , 0.454554
2.995 , -1.07544e-12
2.98697 , -0.454241
2.96423 , -0.809225
2.92778 , -1.09182
2.85429 , -1.39473
2.76893 , -1.59036
2.56493 , -1.82378
2.26318 , -1.95528
1.846 , -1.99616
0 , -2

 

dubins 曲线测试（用于hybridAstar路径规划）

E:\QtCode\cleanPackTest\main\hybrid_astar_annotation

注意更改最小转弯半径，这个半径在生成路径的时候直接就是这个半径，不存在什么最大最小半径；

 

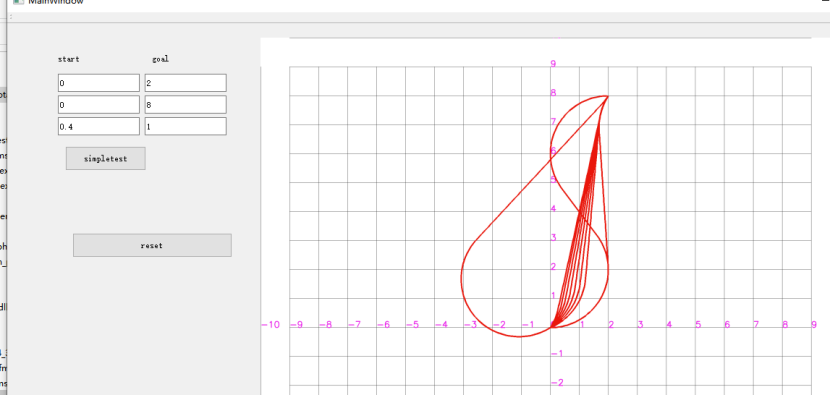
运行CppRobotics测试贝塞尔曲线功能；

E:\QtCode\cppRoboticsTest\tests

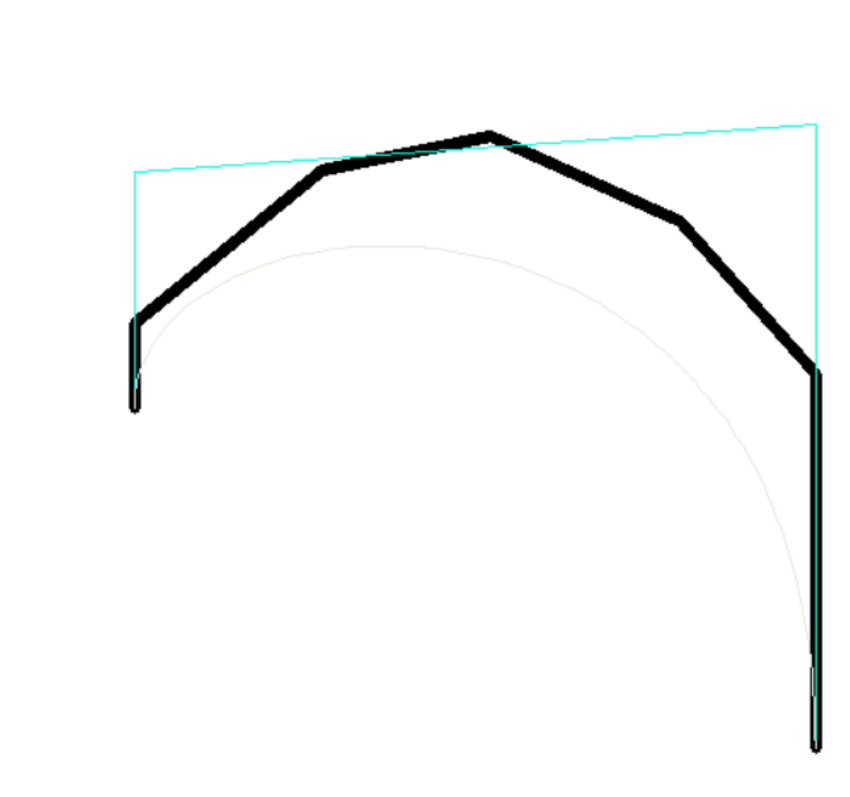
真实环境中可以每两段进行拟合，去掉轨迹上的尖角；

 

运行CppRobotics测试Bspline曲线功能(参数可以修改)

 

 

样条曲线

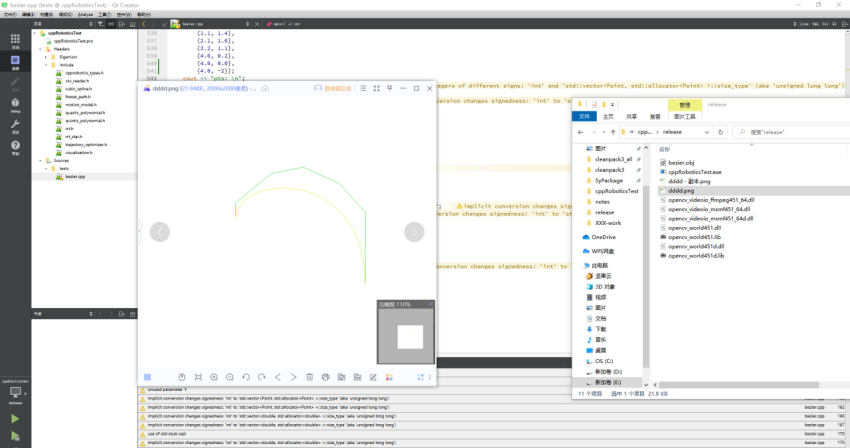
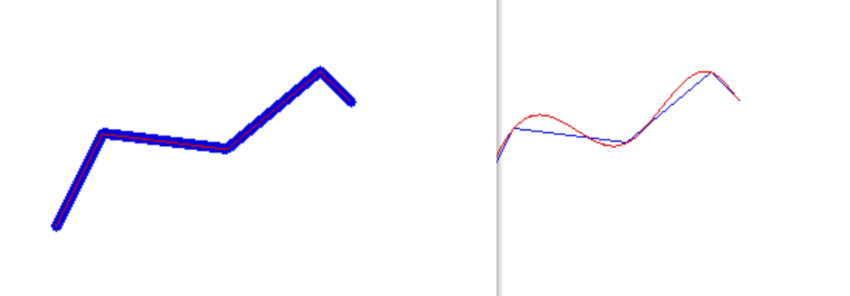
测试usage

tests\cubic_spline_lib_test.cpp

 

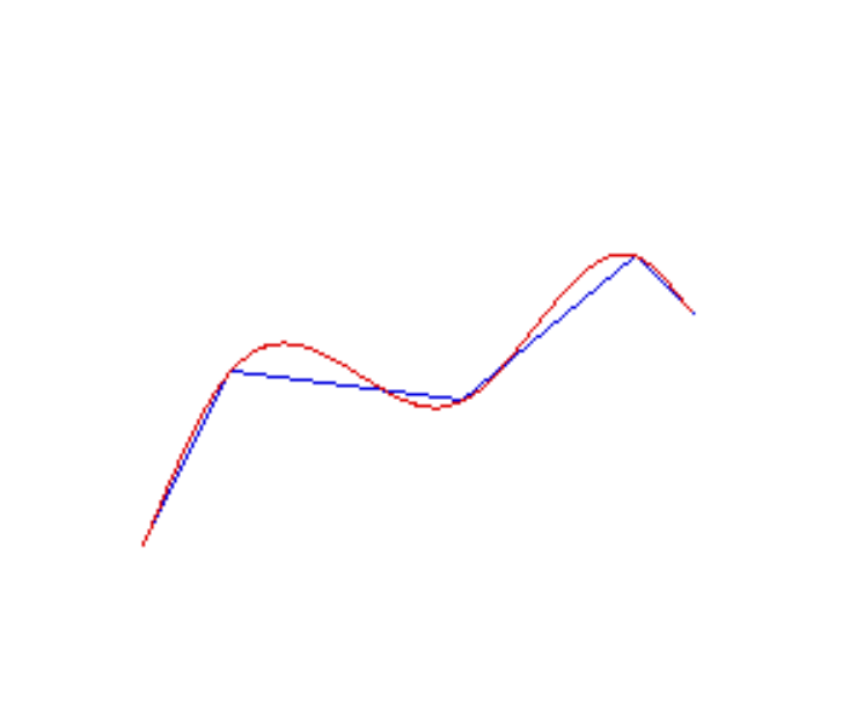
线性插值/C1连续、C2连续

 

 

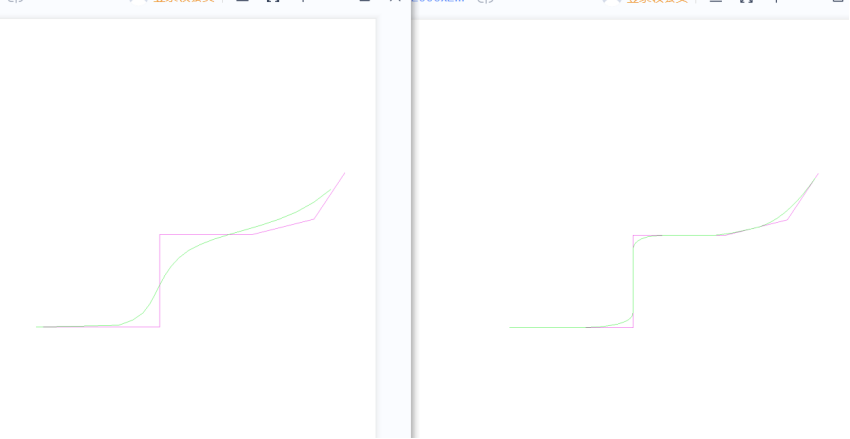
单调性保持

 

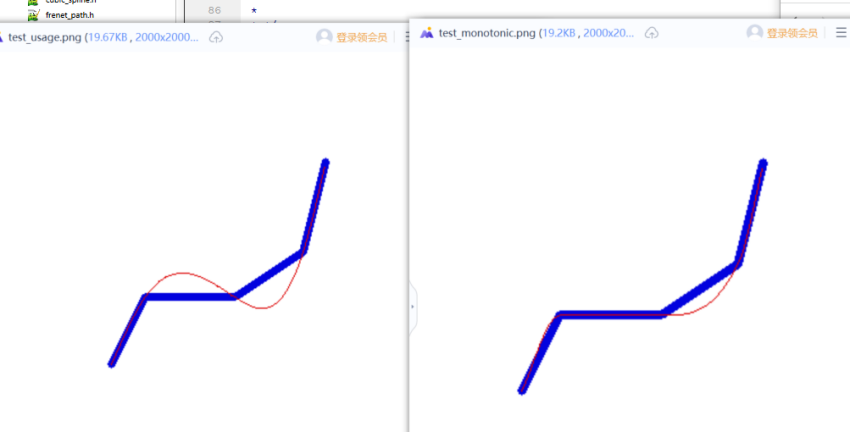
上图中，原始数据是单调的，拟合的曲线也保持单调性;

右边这个图的方法可以保证钝角转弯的地方圆弧过渡；

 

设置边界条件，左右的一阶导和二阶导数（曲率）

 

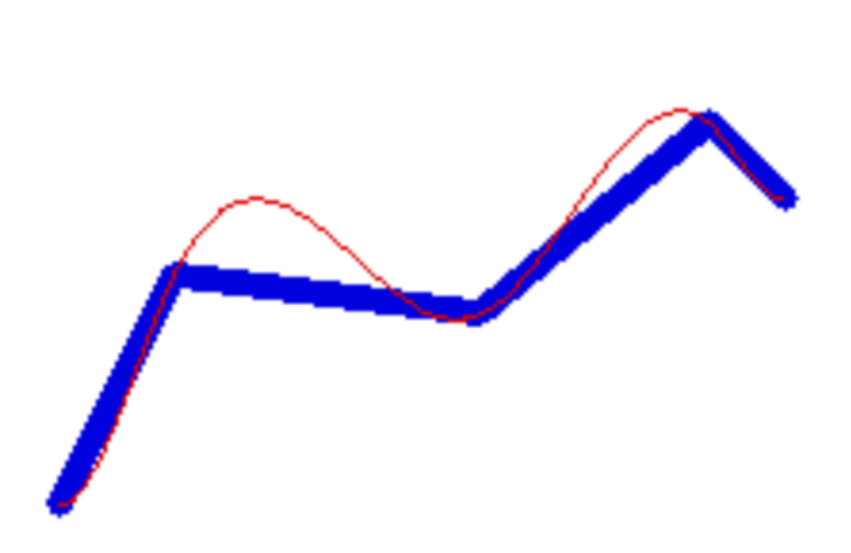
上面这个是设置一阶导为零，也就是起点和终点是平的；

上面这个图的效果可以保证起点和终点的方向在出发和到终点的时候连续调节，去掉原地转向功能；

 

 

 

 

上面这个是设置一阶导数为1.0；

 

平均值保持

曲线的积分和直方图积分一致，对直方图累计拟合曲线，曲线微分就是图中的曲线；

 

 

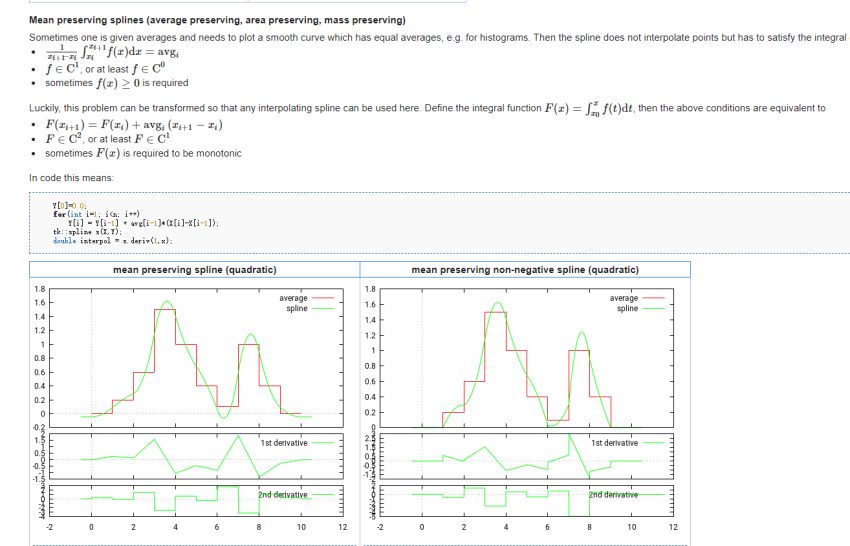
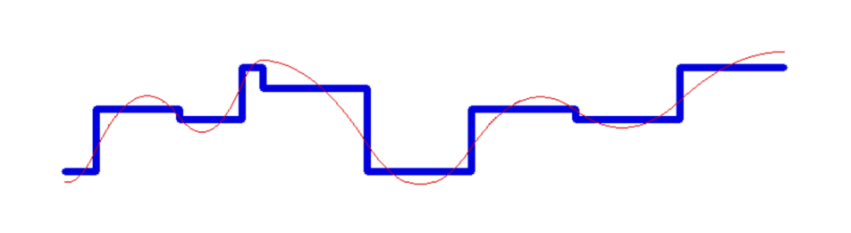
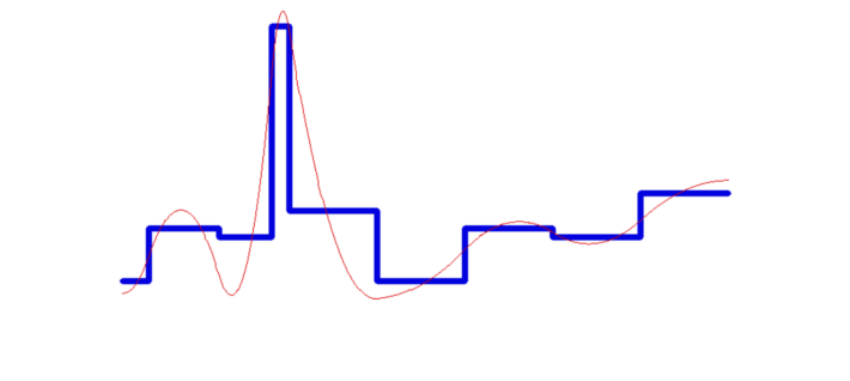
上图对于这种孤峰比较高的情况会导致峰两侧降低的很厉害，补偿作用

 

 

 

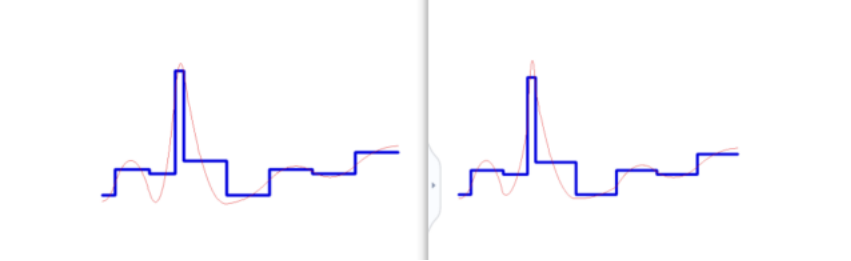
上图spline 改成单调保持，可以避免负值的出现；一阶导数始终为正数；

tk::spline s(X,sum,tk::spline::cspline,true);

 

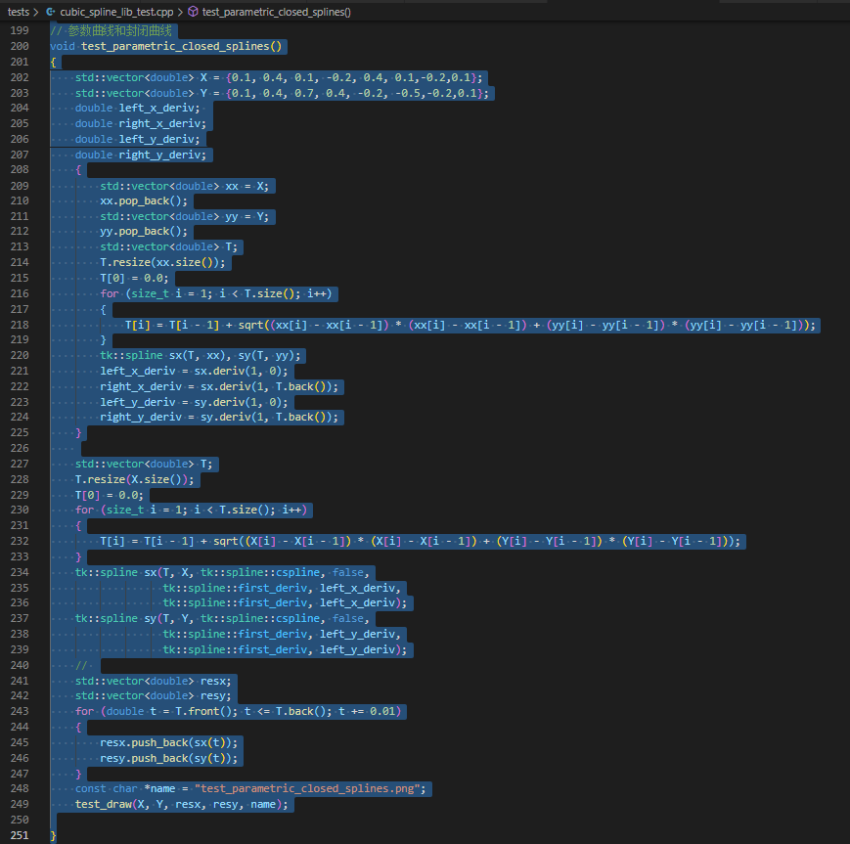
参数化样条曲线

 

 

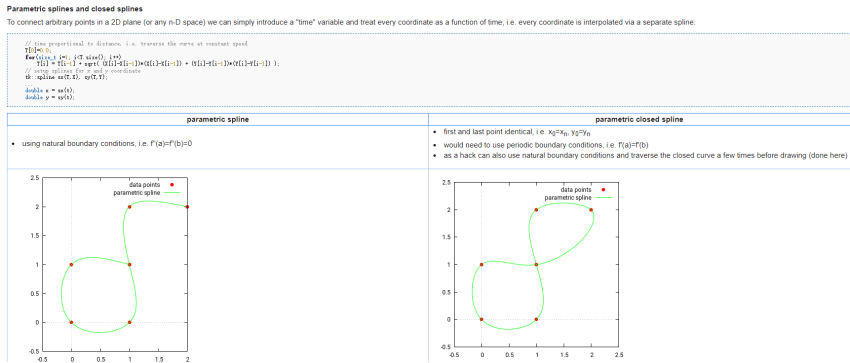
上图是参数化样条

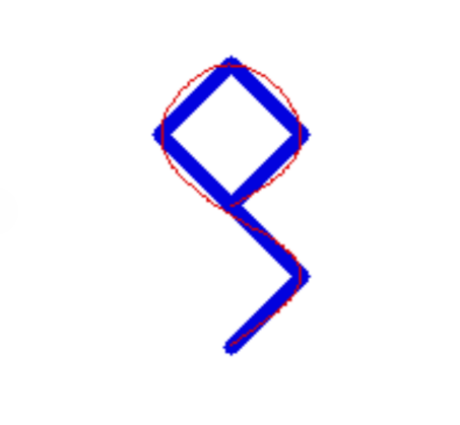
参数化样条封闭曲线

增加终点坐标设置为起点坐标，先计算设置前起点的一阶导数，然后将其作为起点和终点的一阶导边界条件；

 

 

 

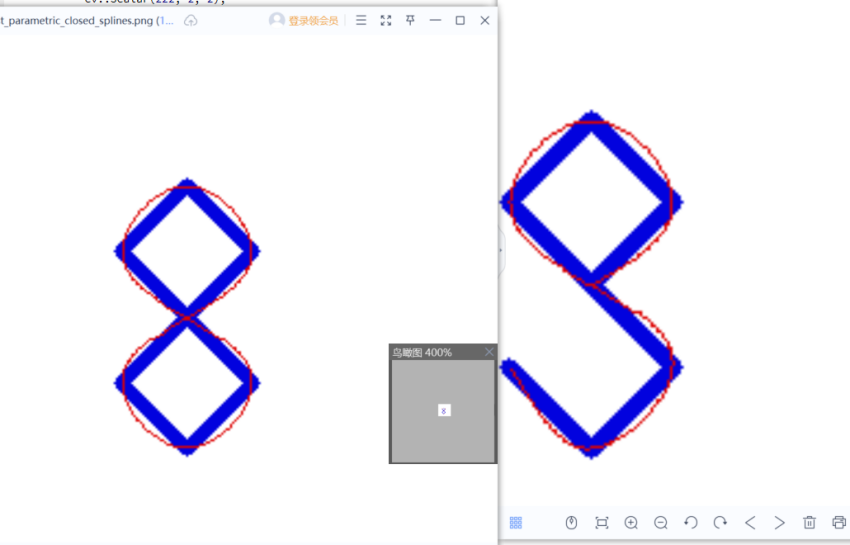
上图是封闭曲线的实现

上图的曲线跟踪可以有效验证轮子速度跟随的有效性；

 

 

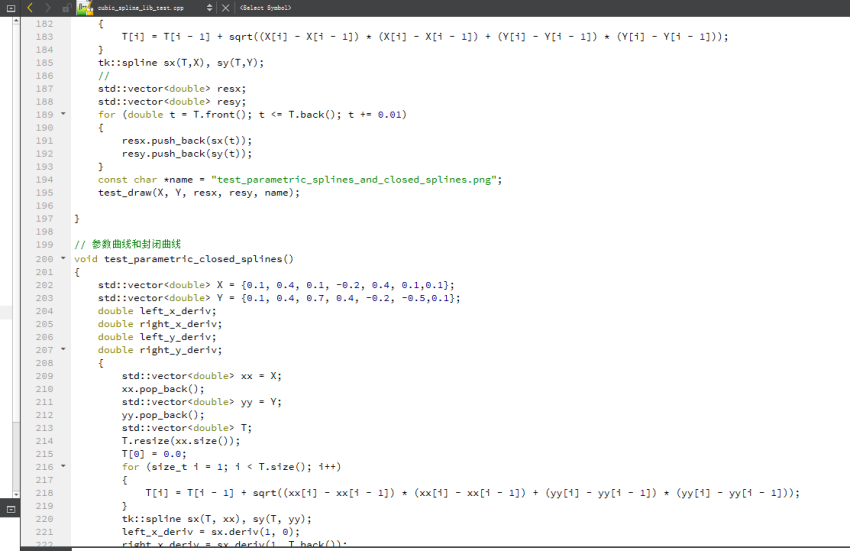
曲率的计算（参考之前spline_planner/cubic_spline.h）

需要计算一阶导数和二阶导数；
float calc_curvature(float s_t)
{
float dx  = sx.calc_d(s_t);
float ddx = sx.calc_dd(s_t);
float dy  = sy.calc_d(s_t);
float ddy = sy.calc_dd(s_t);
return (ddy * dx - ddx * dy) / powf((dx * dx + dy * dy),1.5); // 计算曲率