火车站台连锁店（题解）

火车站台连锁店 首先这道题是一道二分经典题（很难很难）

我们为什么要用二分呢，因为每一次选择数字，无论偏大还是偏小，都可以让剩下的选择范围缩小一半

我们先来看看题目及范围

 

 

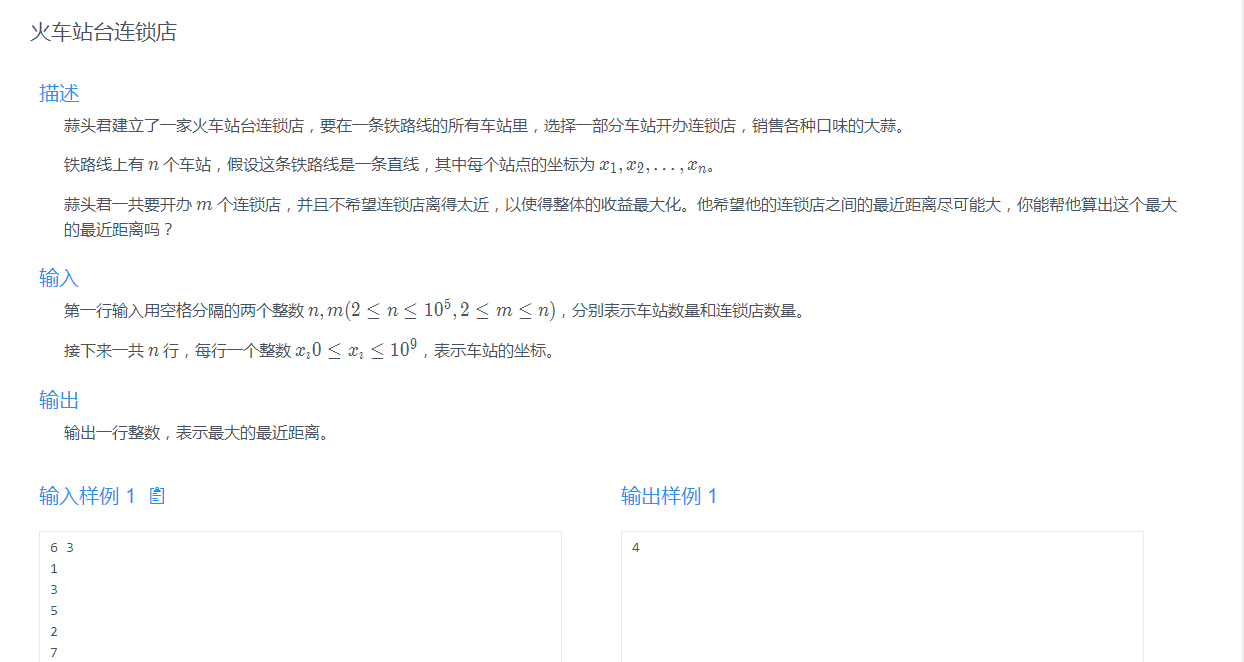
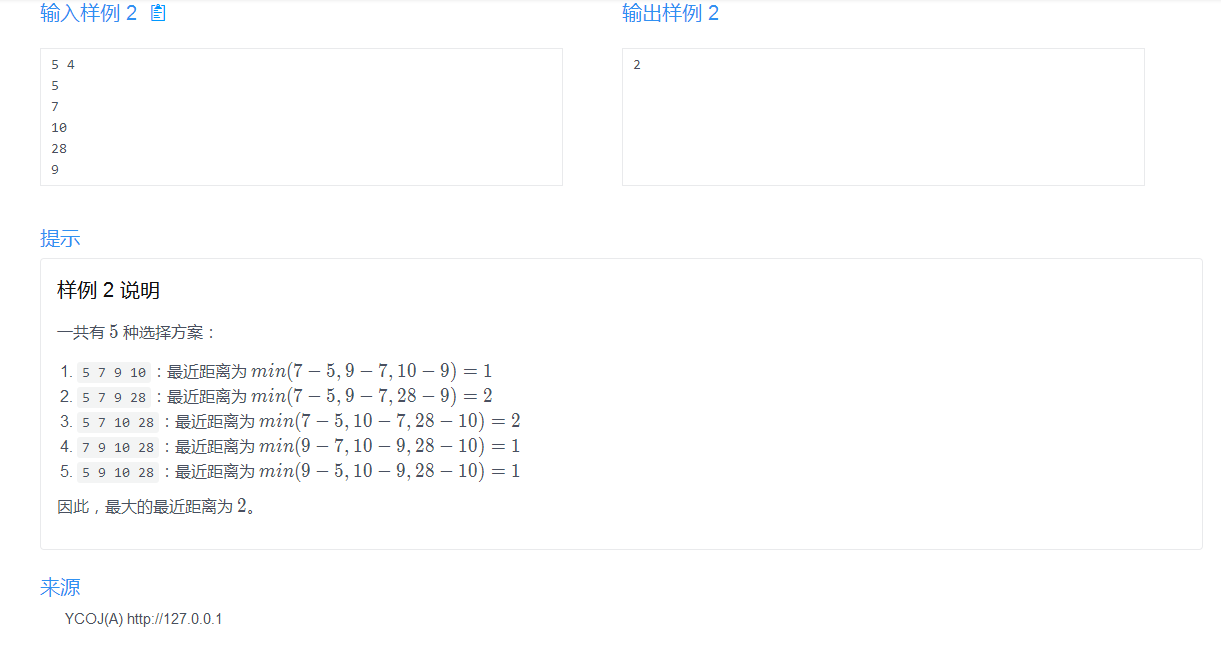
先来看看题目的意思：

大概的意思是我们要让这n个站台中的m个站台里，让每两个站台间的距离都尽可能的大。

因为这道题要求输出最大的最近距离，所以我们就来二分距离。

但是我们需要一个辅助函数bool来计算最短距离能开设多少家店。

bool ok(int x)
{
    int tot = 1;
    int last = 1;
    for(int i = 1; i <= n; i++)
    {
        while(a[i]-a[last] < x)
        {
            i++;
            if(i > n)
            {
                return tot >= m;
            }
        }
        last = i;
        tot++;
    }
    return tot >= m;
}

我们用tot和last这两个临时变量来储存我们的数据（个人喜好）

 

怎么实现查找？
首先确定初始范围
因为我们要把最短距离进行二分查找，所以我们需要一个最初始的left以及right的值。可以肯定的是,这个最短距离L一定在1~最大坐标-最小坐标。

 

通过几次查找，如果我们不停下来的话，left，right，mid三个值都不会再发生变化

因为我们的二分写发是

while（left<right）

因为我们二分的写法是每次left和right其一等于mid，但当它们其中一个和mid相等的时候，这就会成为一个死循环

所以我们就需要改成

while(right - left > 1)

 

 

完整代码如下

#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[100010];
bool ok(int x)
{
    int tot = 1;
    int last = 1;
    for(int i = 1; i <= n; i++)
    {
        while(a[i]-a[last] < x)
        {
            i++;
            if(i > n)
            {
                return tot >= m;
            }
        }
        last = i;
        tot++;
    }
    return tot >= m;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    sort(a+1,a+1+n);
    int l = 0, r = a[n]-a[1];
    while(r-l>1)
    {
        int mid=(l+r)/2;
        if(ok(mid))
        {
            l = mid;
        }
        else
        {
            r = mid;
        }
    }
    if(!ok(r))
    {
        r = l;
    }
    cout << r;
    return 0;
}

顺便一说：

老大在天上一定也有篮球吧，今天是你的纪念日，一路走好。