P1379题解报告

这是一个五年级蒟蒻的第 11 篇题解，望通过。

我将挑战用四种方法 AC 此题，先放一个题目传送门。

F1-BFS

这道题是一种经典的最短路径题，每次操作都会让步数加一，所以考虑 BFS。

写搜索题，最重要的就是状态和转移。显然，这道题的状态是目前的八数码和走过的步数。

但是问题显现，八数码如何存储呢？

• 我会 STL，我用 map。可以定义一个结构体 node，就是一个二维数组，加上比较函数（没有这个，map 就不能运行），定义一个 map<node, int> 表示每个八数码走了多少步。
• 我会 hash，可以将每个八数码映射成一个数，同样用 map 存储。
• 我会康托展开，将一个八数码看成一个 \(0 \sim 9\) 的全排列，然后套用康托展开的公式，用数组存储即可。
• 我啥都不会，但是我可以将一个八数码的 \(9\) 位拼在一起变成一个 \(9\) 位数，用 map 即可。

所以有了状态，转移就很好想了，每次交换 \(0\) 与它旁边的位置，步数加一即可。

复杂度：时间和空间都是 \(9!\)，可以通过。

code

这里采用第一种方法，结构体 \(+\) map。

#include<bits/stdc++.h>

using namespace std;

const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};

struct node{
  int a[3][3];
  bool operator < (node b) const{
    for(int i = 0; i < 3; i++){
      for(int j = 0; j < 3; j++){
        if(a[i][j] != b.a[i][j])
          return a[i][j] < b.a[i][j];
      }
    }
    return 0;
  }
}s, t;

queue<node> q;
map<node, int> mp;

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  t.a[0][0] = 1, t.a[0][1] = 2, t.a[0][2] = 3;
  t.a[1][0] = 8, t.a[1][1] = 0, t.a[1][2] = 4;
  t.a[2][0] = 7, t.a[2][1] = 6, t.a[2][2] = 5;
  string str;
  cin >> str;
  for(int i = 0; i < 3; i++){
    for(int j = 0; j < 3; j++){
      s.a[i][j] = str[i * 3 + j] - '0';
    }
  }
  q.push(s);
  mp[s] = 0;
  while(q.size()){
    node u = q.front();
    q.pop();
    int x, y;
    for(int i = 0; i < 3; i++)
      for(int j = 0; j < 3; j++)
        if(!u.a[i][j])
          x = i, y = j;
    for(int i = 0; i < 4; i++){
      node v = u;
      int xx = x + dx[i], yy = y + dy[i];
      if(0 <= xx && xx < 3 && 0 <= yy && yy < 3){
        swap(v.a[x][y], v.a[xx][yy]);
        if(!mp.count(v)){
          mp[v] = mp[u] + 1;
          q.push(v);
        }
      }
    }
  }
  cout << mp[t];
  return 0;
}

于是，你就愉快的 AC 了。走了走了不看后面了。

F2-双向 BFS

个人认为，双向 BFS 是一种较为冷门的算法，它通过空间换时间的方法降低了时间复杂度。

双向广搜，顾名思义，就是从起点和终点两个方向进行广搜，直到它们相遇。为什么复杂度会降低呢？这里放一张图片（画得有点丑，见谅）：

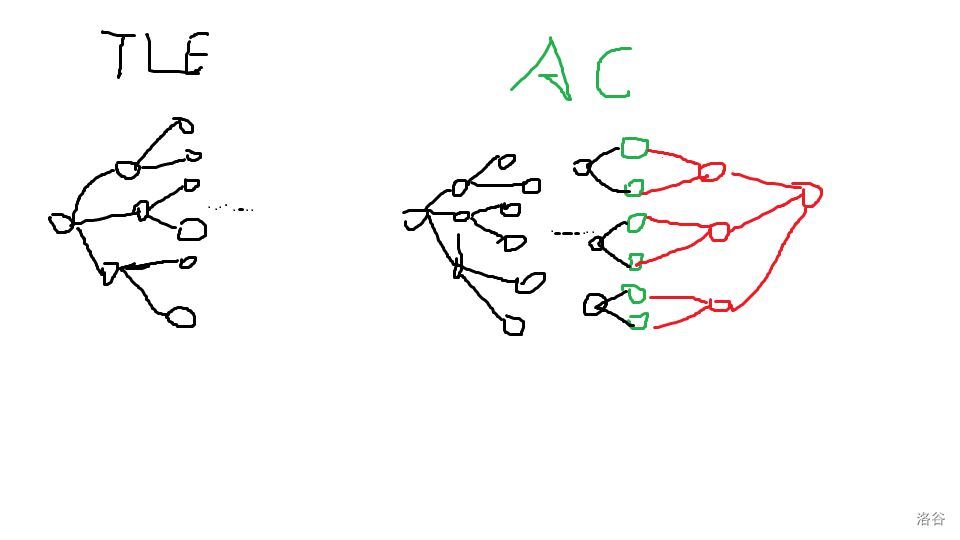
我们发现，两个点同时进行广搜，会比直接广搜复杂度低，因为省去了许多不必要的分支。

状态和转移和 F1 一样，我们讲一讲具体实现。

我们可以开两个队列，分别表示从起点扩张的情况和从终点扩张的情况。标记还是用两个 map，表示起点扩张和终点扩张。我们交替扩张，对于每次扩张，可以取出队头，进行扩张。如果扩出的状态已经在另一个 map 中被标记，那么在两个 map 中的答案之和就是最终的答案。如果还不懂的话，请移步代码。

code

#include<bits/stdc++.h>

using namespace std;

const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};

struct node{
  int a[3][3];
  bool operator < (node b) const{
    for(int i = 0; i < 3; i++){
      for(int j = 0; j < 3; j++){
        if(a[i][j] != b.a[i][j])
          return a[i][j] < b.a[i][j];
      }
    }
    return 0;
  }
}s, t;

queue<node> q1, q2;
map<node, int> mp1, mp2;

void r(queue<node> &q, map<node, int> &m1, map<node, int> &m2){
  if(!q.size()) return;
  node u = q.front(); 
  q.pop();
  int x, y;
  for(int i = 0; i < 3; i++)
    for(int j = 0; j < 3; j++)
      if(!u.a[i][j])
        x = i, y = j;
  for(int i = 0; i < 4; i++){
    node v = u;
    int xx = x + dx[i], yy = y + dy[i];
    if(0 <= xx && xx < 3 && 0 <= yy && yy < 3){
      swap(v.a[x][y], v.a[xx][yy]);
      if(m2.count(v)){
      	cout << m1[u] + m2[v] + 1;
      	exit(0);
      }
      if(!m1.count(v)){
        m1[v] = m1[u] + 1;
        q.push(v);
      }
    }
  }
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  t.a[0][0] = 1, t.a[0][1] = 2, t.a[0][2] = 3;
  t.a[1][0] = 8, t.a[1][1] = 0, t.a[1][2] = 4;
  t.a[2][0] = 7, t.a[2][1] = 6, t.a[2][2] = 5;
  string str;
  cin >> str;
  if(str == "123804765") return cout << 0, 0;
  for(int i = 0; i < 3; i++){
    for(int j = 0; j < 3; j++){
      s.a[i][j] = str[i * 3 + j] - '0';
    }
  }
  q1.push(s);
  mp1[s] = 0;
  q2.push(t);
  mp2[t] = 0;
  while(1){
    r(q1, mp1, mp2);
    r(q2, mp2, mp1);
  }
  return 0;
}

F3-A*

A* 搜索算法（A* search algorithm，A* 读作 A-star），简称 A* 算法，是一种在带权有向图上，找到给定起点与终点之间的最短路径的算法。它属于图遍历（graph traversal）和最佳优先搜索算法（best-first search），亦是 BFS 的改进。——摘自 OI-Wiki

在 A* 算法中，对于每一个状态 \(x\)，我们设从起点经过它的估计总路程为 \(f(x)\)，从起点走到此状态的答案为 \(g(x)\)，\(h(x)\) 为当前状态到目标状态的一个估计，则

\[f(x) = g(x) + h(x) \]

在 A* 算法中，我们将普通队列换成优先队列，每次取出 \(f(x)\) 最小的状态进行扩张，并利用真实的 \(g(x)\) 更新 \(f(x)\)。

在此题中，我们将 \(h(x)\) 定义为目前的八数码和目标状态之间的曼哈顿距离即可，不能加 0，会 WA！

我们定义两个结构体，一个判重用，一个优先队列里用，第一个结构体与前面一样，第二个结构体中为一个状态，一个 \(g(x)\)，一个函数 \(h(x)\) 和比较器（用于优先队列）。A* 的实现就不多说了，理解上面的。

code

#include<bits/stdc++.h>

using namespace std;

const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0}, pos[9][2] = {{2, 2}, {0, 0}, {0, 1}, {0, 2}, {1, 2}, {2, 2}, {2, 1}, {2, 0}, {1, 0}};

struct node{
  int a[3][3];
  bool operator < (node b) const{
    for(int i = 0; i < 3; i++){
      for(int j = 0; j < 3; j++){
        if(a[i][j] != b.a[i][j])
          return a[i][j] < b.a[i][j];
      }
    }
    return 0;
  }
}s, t;

struct Node{
  int dis;
  node x;
  int h() const{
    int ans = 0;
    for(int i = 0; i < 3; i++){
      for(int j = 0; j < 3; j++){
        if(!x.a[i][j]) continue;
        ans += abs(i - pos[x.a[i][j]][0]) + abs(j - pos[x.a[i][j]][1]);
      }
    }
    return ans;
  }
  bool operator < (Node y) const{
    return dis + h() > y.dis + y.h();
  }
};

priority_queue<Node> q;
map<node, int> mp;

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  t.a[0][0] = 1, t.a[0][1] = 2, t.a[0][2] = 3;
  t.a[1][0] = 8, t.a[1][1] = 0, t.a[1][2] = 4;
  t.a[2][0] = 7, t.a[2][1] = 6, t.a[2][2] = 5;
  string str;
  cin >> str;
  if(str == "123804765") return cout << 0, 0;
  for(int i = 0; i < 3; i++){
    for(int j = 0; j < 3; j++){
      s.a[i][j] = str[i * 3 + j] - '0';
    }
  }
  mp[s] = 0;
  q.push({0, s});
  while(q.size()){
    if(!q.top().h()){
      cout << q.top().dis;
      break;
    }
    node u = q.top().x;
    q.pop();
    int x, y;
    for(int i = 0; i < 3; i++)
      for(int j = 0; j < 3; j++)
        if(!u.a[i][j])
          x = i, y = j;
    for(int i = 0; i < 4; i++){
      node v = u;
      int xx = x + dx[i], yy = y + dy[i];
      if(0 <= xx && xx < 3 && 0 <= yy && yy < 3){
        swap(v.a[x][y], v.a[xx][yy]);
        if(!mp.count(v)){
          mp[v] = mp[u] + 1;
          q.push({mp[v], v});
        }
      }
    }
  }
  return 0;
}

F4-IDA*

IDA* 是 IDDFS 与 A* 的结合，我们只讲一下 IDDFS。

迭代加深搜索本质是深搜，但它限定了深度，一旦当前搜索深度大于或等于限定深度，就立刻回溯，如果当前限制的深度有答案就直接结束，如果没有就放宽限制。
有人就会问：在限定新深度时，浅深度的状态会被枚举很多次，会不会浪费时间导致 \(T\) 飞？
我的回答是：这个得具体情况具体分析，当一个状态能转移出的状态不多时，在枚举新限定深度时，需要记录上一层状态；但如果转移状态是指数级的增长时，就没必要，因为前几层的状态在后几层来说就是九牛一毛，记状态也快不了多少。
迭代加深弥补了广搜的空间开销太大，也弥补了深搜的无底洞，是一个好算法。——摘自我的第一篇题解

关于 IDDFS 的实现，可以参考我的第一篇题解的不过样例的实现。

IDA* 就是在 IDDFS 的基础上跑 A*，只是把层数上限改为 \(f(x)\) 的上限。这里使用 map 去重，记得 erase。

code

#include<bits/stdc++.h>

using namespace std;

const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0}, pos[9][2] = {{2, 2}, {0, 0}, {0, 1}, {0, 2}, {1, 2}, {2, 2}, {2, 1}, {2, 0}, {1, 0}};

struct node{
  int a[3][3];
  bool operator < (node b) const{
    for(int i = 0; i < 3; i++){
      for(int j = 0; j < 3; j++){
        if(a[i][j] != b.a[i][j])
          return a[i][j] < b.a[i][j];
      }
    }
    return 0;
  }
}s, t;

int depth;
map<node, int> mp;

int h(node x){
  int ans = 0;
  for(int i = 0; i < 3; i++){
    for(int j = 0; j < 3; j++){
      int num = x.a[i][j];
      if(!num) continue;
      ans += abs(i - pos[num][0]) + abs(j - pos[num][1]);
    }
  }
  return ans;
}

void dfs(int dep, node u){
  int cnt = h(u);
  if(!cnt){
    cout << depth;
    exit(0);
  }
  if(dep + cnt > depth) return;
  mp[u] = 1;
  int x, y;
  for(int i = 0; i < 3; i++)
    for(int j = 0; j < 3; j++)
      if(!u.a[i][j])
        x = i, y = j;
  for(int i = 0; i < 4; i++){
    node v = u;
    int xx = x + dx[i], yy = y + dy[i];
    if(0 <= xx && xx < 3 && 0 <= yy && yy < 3){
      swap(v.a[x][y], v.a[xx][yy]);
      if(!mp.count(v)) dfs(dep + 1, v);
    }
  }
  mp.erase(u);
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  t.a[0][0] = 1, t.a[0][1] = 2, t.a[0][2] = 3;
  t.a[1][0] = 8, t.a[1][1] = 0, t.a[1][2] = 4;
  t.a[2][0] = 7, t.a[2][1] = 6, t.a[2][2] = 5;
  string str;
  cin >> str;
  for(int i = 0; i < 3; i++){
    for(int j = 0; j < 3; j++){
      s.a[i][j] = str[i * 3 + j] - '0';
    }
  }
  for(; ; depth++){
    mp.clear();
    dfs(0, s);
  }
  return 0;
}